数学北师大版1 两条直线的位置关系教课内容ppt课件

这是一份数学北师大版1 两条直线的位置关系教课内容ppt课件，共15页。PPT课件主要包含了相交线与平行线的概念，公共边，邻补角，余角和补角的概念，课本习题21等内容，欢迎下载使用。
AB∥CD 或 a∥b
直线AB和直线CD相交于点O
相交线：在同一平面内，若两条直线只有一个公共点， 我们称这两条直线为相交线平行线：在同一平面内，不相交的两条直线叫做平行 线（直线AB∥CD或直线a∥b)在同一平面内，两条直线的位置关系只有平行和相交两种
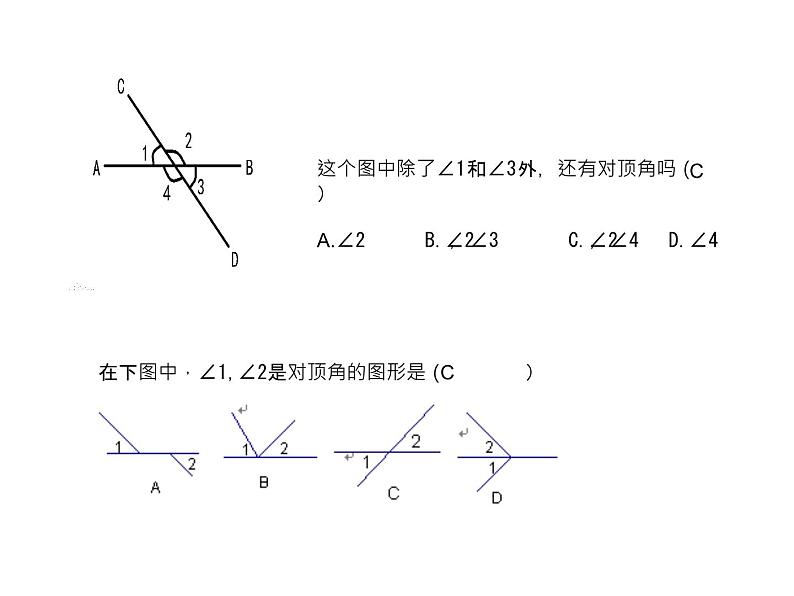
这个图中除了∠1和∠3外，还有对顶角吗（ ）A.∠2 B.∠2，∠3 C.∠2，∠4 D.∠4
在下图中，∠1,∠2是对顶角的图形是（ ）
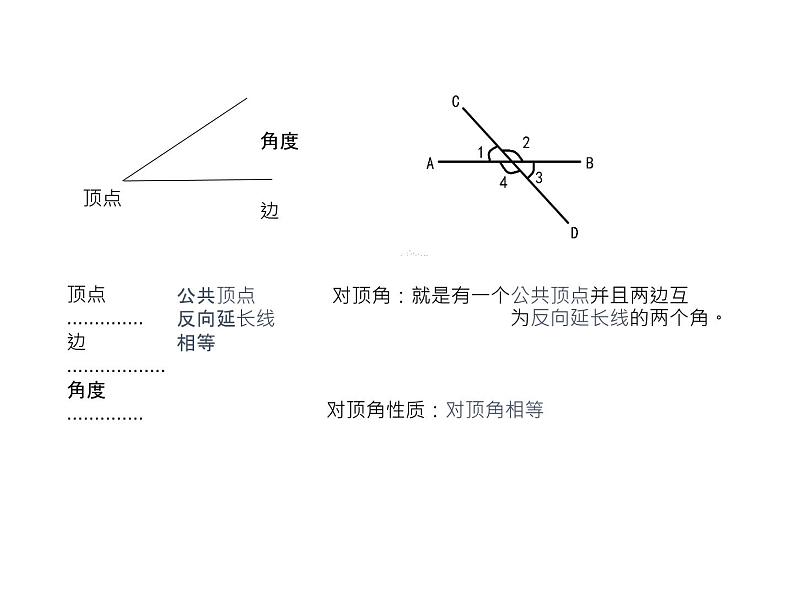
对顶角：就是有一个公共顶点并且两边互 为反向延长线的两个角。
对顶角性质：对顶角相等

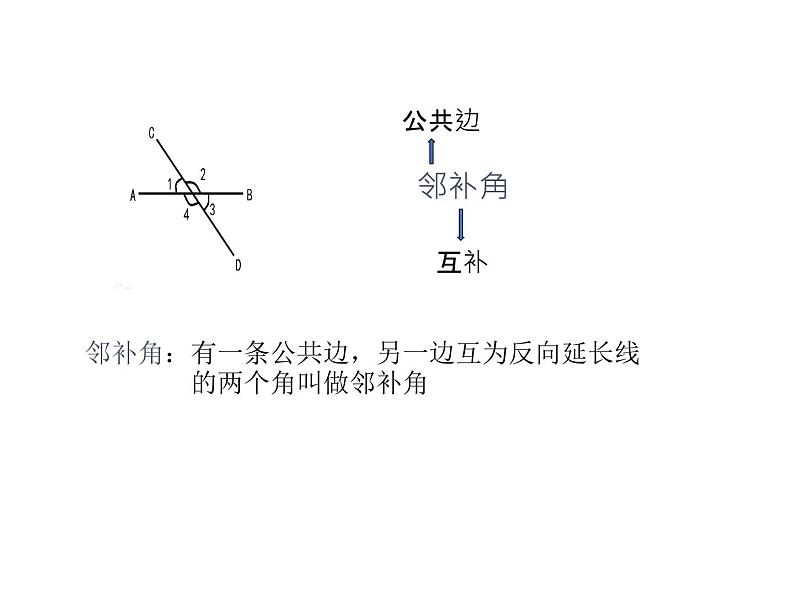
邻补角：有一条公共边，另一边互为反向延长线 的两个角叫做邻补角
补角：如果两个角的和为180°就说这两个角互 为补角，或称这两个角互补，其中一个角 是另一个角的补角。 （∠2+∠3=180°则∠2与∠3互补）余角：如果两个角的和等于90°，就说 这两个角互为余角，或称这两个角互余， 其中一个角是另一个角的余角。 （∠1+∠2=90°则∠1与∠2互余）互余和互补：两个角的度数关系
同角的余角相等，等角的余角相等。同角的补角相等，同角的补角相等。
∵∠1+∠2=90° ∠1+∠3=90°∵∠1=∠1∴∠2=∠3∴同角的余角相等
∵∠1+∠3=90° ∠4+∠3=90°∴∠1=∠4∵∠1+∠2=90° ∠4+∠3=90°∴∠2=∠3∴等角的余角相等
∵ ∠1+∠2=180° ∠3+∠2=180° ∵ ∠2=∠2 ∴ ∠1=∠3 ∴ 同角的补角相等 ∵ ∠1+∠2=180° ∠3+∠4=180° ∵∠1=∠3 ∴∠2=∠4 ∴等角的补角相等
同角或等角的余角相等，同角或等角的补角相等。
1、42°角的余角是多少？ 解： 90°-42°=48° 2、56°角的余角的补角是多少？ 解：90°-56°=34° 180°-34°=146°
3、一个锐角的补角比它的余角大多少？
猜想：如果它是20° 补角180°-20°=160° 余角 90°-20°=70° 补角比余角大160°-70°=90°
如果它是72°补角180°-72°=108°余角 90°-72°=18°补角比余角大108°-18°=90°
解：设这个锐角为X 补角180°-X 余角 90°-X 补角比余角大（180°-X）-（90°-X ）=90°
利用对顶角和邻补角求角度直线AB、CD交于点O，射线OM平分∠AOC，∠BOD=76°，则∠BOM=？
∵∠BOC与∠BOD互为邻补角∴∠BOC=180°－∠BOD=180°－76°=104°∵OM是角的平分线∴∠COM=½∠COA∵∠COA=∠BOD=76°∴∠COM=38°∴∠BOM=∠BOC+∠COM=104°+38°=142°
一、同一平面内两条直线的位置关系二、余角、补角、对顶角、邻补角的概念三、余角、补角、对顶角的性质