






初中数学浙教版八年级上册第2章 特殊三角形2.7 探索勾股定理精品ppt课件
展开1. 探索并掌握定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.2. 会用上述定理判定一个三角形是不是直角三角形.
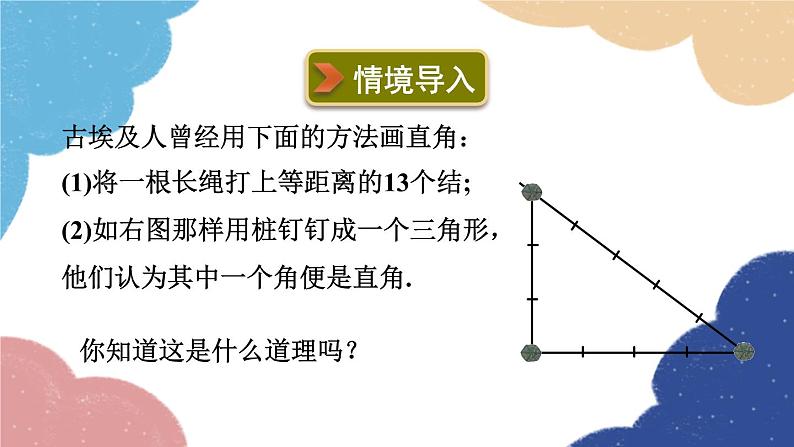
古埃及人曾经用下面的方法画直角:(1)将一根长绳打上等距离的13个结;(2)如右图那样用桩钉钉成一个三角形,他们认为其中一个角便是直角.
你知道这是什么道理吗?
一个三角形满足什么条件才能是直角三角形呢?
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和为90°的三角形是直角三角形;
如果一个三角形的三边a,b,c满足a2+b2=c2, 那么这个三角形是直角三角形吗?
试画出三边长度分别为如下数据的三角形,看看它们是一些什么样的三角形:(1) a = 3,b = 4,c = 5;(2) a = 4,b = 6,c = 8;(3) a = 6,b = 8,c = 10.
按(1)、(3)所画的三角形是直角三角形,而按(2)画的不是.
(1)、(3)两组数据有什么特点?
32 +42 ____ 52
较短的两条边的平方和_____最长边的平方.
最长边所对的角是_____.
52 +122 ____ 132
根据你所画的三角形及计算结果填空:
勾股定理的逆定理 如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
即如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形,且边c所对的角为直角.
提示:可作一个与△ABC全等的直角三角形,利用全等的性质来说明∠C是直角.
你能尝试证明这个定理吗?
已知:如图,在△ABC中,AB=c,BC=a,CA=b,a2+b2=c2.
求证:∠C =90°.
例1.判断由线段a,b,c组成的三角形是不是直角三角形.若是,指出哪一条边所对的角是直角.(1) a=15,b=8,c=17;(2) a=13,b=14,c=15.
解: (1) ∵82+152=289,172=289, ∴82+152=172,即a2+b2=c2. ∴由线段a,b,c组成的三角形是直角三角形. 其中,c所对的角是直角.
直角三角形中最长边所对的角为直角.
解: (2) ∵132+142=169+196=365,152=225, ∴132+142≠152. 即a2+b2≠c2, ∴由线段a,b,c组成的三角形不是直角三角形.
例2.已知 △ABC,AB= n2 - 1,BC= 2n,AC = n2+1 (n为大于1的正整数).试问△ ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由.
∴△ABC是直角三角形,边AC所对的角是直角.
解:∵AB2 + BC2 = (n2 -1)2 + (2n)2 =n4 - 2n2 + 1 + 4n2 =n4 + 2n2 + 1 =(n2 + 1) 2 =AC2,
1.下列长度的三条线段,能组成直角三角形的是( ) A.2,2,4 B.5,6,12 C.5,7,2 D.6,8,10
2.一个三角形的三边长分别为a2+b2,a2-b2,2ab,则这个三角形的形状为( ) A.钝角三角形 B.直角三角形C.锐角三角形 D.形状不能确定
3.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )A.7.5平方千米 B.15平方千米C.75平方千米 D.750平方千米
4.已知a、b、c分别为△ABC的三边长,且满足|a-12|+(c-13)2+(b-5)2=0 ,试判断△ABC的形状.
解:∵ |a-12|+(c-13)2+(b-5)2=0,∴ |a-12|=0,(c-13)2 =0,(b-5)2=0, ∴ a-12=0,c-13=0,b-5=0. 即a=12,c=13,b=5.又∵ a2+b2=122+52=169,且c2=169,∴ a2+b2=c2,∴ △ABC是直角三角形.
勾股定理的逆定理 如果三角形中________________________________,那么这个三角形是直角三角形.即如果三角形的三边长a、b、c有关系__________,那么这个三角形是直角三角形,且边c所对的角为直角.
两边的平方和等于第三边的平方
初中浙教版2.7 探索勾股定理课前预习ppt课件: 这是一份初中浙教版2.7 探索勾股定理课前预习ppt课件,共17页。PPT课件主要包含了勾股定理,勾股定理的逆定理,直角三角形的判定方法,合作探究等内容,欢迎下载使用。
数学八年级上册2.7 探索勾股定理课文内容课件ppt: 这是一份数学八年级上册2.7 探索勾股定理课文内容课件ppt,共25页。PPT课件主要包含了∴a2+b2c2,a+b2,c2+,也可以表示为,a2+b2c2,它们之间的关系是,化简得,勾股定理,+x2172,+122x2等内容,欢迎下载使用。
初中数学浙教版八年级上册2.7 探索勾股定理课堂教学课件ppt: 这是一份初中数学浙教版八年级上册2.7 探索勾股定理课堂教学课件ppt,共15页。PPT课件主要包含了比一比谁最快,试一试,显身手,=m2+n22,=c2,练一练,割补法,归纳小结,拓展与应用等内容,欢迎下载使用。













