




初中数学浙教版八年级上册2.8 直角三角形全等的判定评优课ppt课件
展开三条道路两两相交,你能找出一点,使它到三条道路的距离都相等吗?
回顾:要判定两个三角形全等,我们已经有哪些方法?
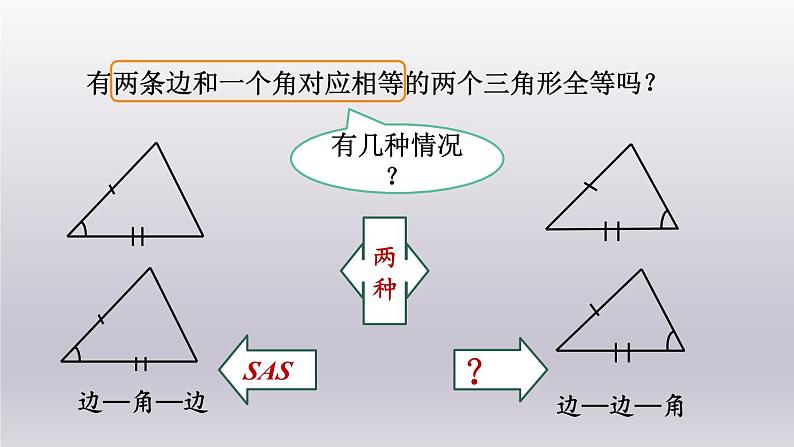
活动探究:(1)有两条边和一个角对应相等的两个三角形全等吗?(2)如果这个角是直角呢?可通过作图、叠合等方法进行探索.
有两条边和一个角对应相等的两个三角形全等吗?
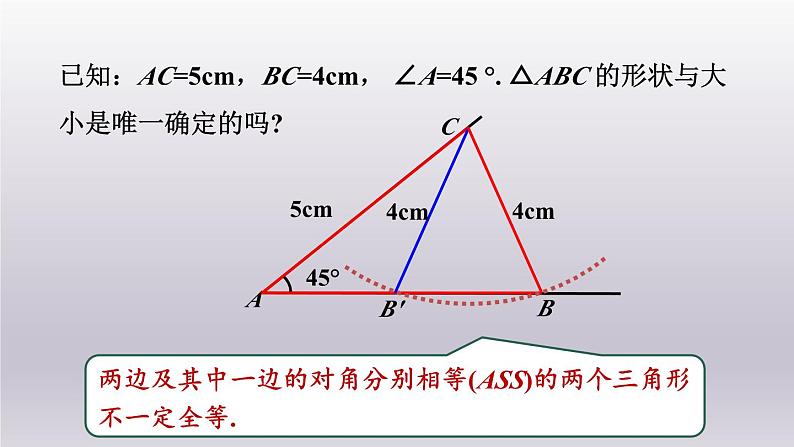
已知:AC=5cm,BC=4cm, ∠A=45 °. △ABC 的形状与大小是唯一确定的吗?
两边及其中一边的对角分别相等(ASS)的两个三角形不一定全等.
实际上,根据勾股定理,已知直角三角形的两边长即可得出第三边的长.然后根据SSS即可判定全等.
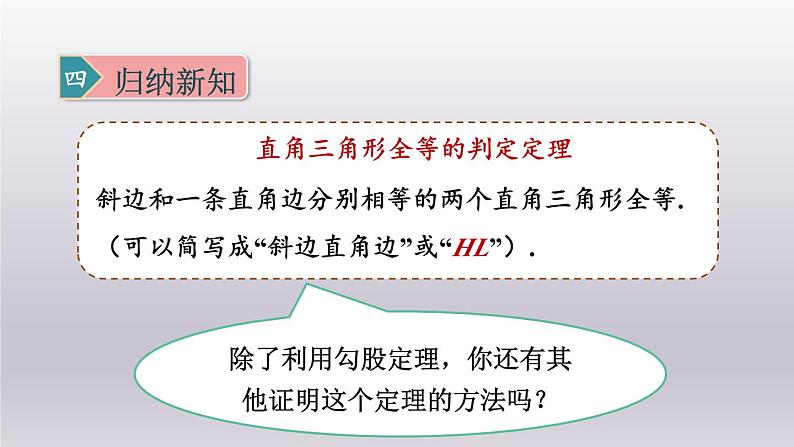
斜边和一条直角边分别相等的两个直角三角形全等.(可以简写成“斜边直角边”或“HL”).
直角三角形全等的判定定理
除了利用勾股定理,你还有其他证明这个定理的方法吗?
已知:如图,在△ACB和△A′C′B′中,∠C=∠C′=Rt∠,AB=A′B′,AC=A′C′.求证:Rt△ABC≌Rt△A′B′C′.
分析:因为AC=A′C′,所以可考虑以AC为一边作个直角三角形,使它和Rt△A′B′C全等,然后只要证明所作的直角三角形和Rt△ABC全等.
证明:如图,延长BC至D,使CD=B′C′,连结AD.∵AC=A′C′ (已知),∠ACD=Rt∠=∠C′, ∴ △ADC≌△A′B′C′ (SAS).∴AD=A′B′ (全等三角形的对应边相等).∵ A′B′=AB (已知) ,又∵AC⊥BD,∴BC=DC (等腰三角形三线合一).而AC=AC (公共边) ,∴△ADC≌△ABC (SSS) ,
∴△ABC≌△A′B′C′.
已知线段a,c(如图),用直尺和圆规作Rt△ABC,使∠C=Rt∠,BC=a,AB=c.
作法:1.画∠MCN=90°;2.在射线CM上取BC=a ;3.以B为圆心,c为半径画弧,交射线CN于点A;4.连接AB.则△ ABC就是所求作三角形.
例 已知:如图,P是∠AOB内一点PD⊥OA,PE⊥OB , D,E分别是垂足,且PD=PE.求证:点P在∠AOB的平分线上.
分析:如图,要证明点P在∠AOB的平分线上,可以转化为证明射线OP平分∠AOB.
证明:如图,作射线OP.∵PD⊥OA,PE⊥OB (已知),∴∠PDO=∠PEO=Rt∠.又∵ OP=OP (公共边),PD=PE (已知) , ∴Rt△PDO≌Rt△PEO (HL).∴ ∠AOP=∠BOP ,即点P在∠AOB的平分线上(角平分线的定义).
角的内部,到角两边距离相等的点,在这个角的平分线上.
角平分线性质定理的逆定理
这个定理的逆定理是:_______________________________,即____________________.
角平分线上的点到角两边距离相等
①分别画出三个角的角平分线;②根据“角的内部,到角两边距离相等的点,在这个角的平分线上”可知交点P到三条道路的距离都相等.
1.如图,AC=BC,AC⊥OA,CB⊥OB,则Rt△AOC≌Rt△BOC的理由是( )A.SSS B.ASA C.SAS D.HL
分析:在Rt△AOC和Rt△BOC中,AC=BC,OC=OC,则Rt△AOC≌Rt△BOC(HL).
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )A.线段CD的中点 B.CD与过点O作CD的垂线的交点 C.CD与∠AOB的平分线的交点 D.以上均不对
3.在△ABC中,BD=CD,DE⊥AB于点E ,DF⊥AC于点F ,且DE=DF,求证:△BED≌△CFD.
证明:∵DE⊥AB,DF⊥AC, ∴∠DEB=∠DFC=90°. ∴△DEB和△DFC是直角三角形.
∴Rt△DEB≌Rt△DFC(HL).
∵ DB=DC,DE=DF,
4.已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
证明:作PD⊥BC于点D,∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,∴PM=PD,同理,PN=PD,∴PM=PN,又∵ PM⊥AB,PN⊥AC,
(1)叙述两个直角三角形全等的判定定理.(2)叙述角平分线性质定理的逆定理.(3)举例说明角平分线性质定理的逆定理在实际生活中的应用.
初中数学浙教版八年级上册2.8 直角三角形全等的判定评课课件ppt: 这是一份初中数学浙教版八年级上册2.8 直角三角形全等的判定评课课件ppt,共14页。PPT课件主要包含了用画图的方法探究,定理证明,SAS,ASA,AAS,SSS,知识小结,ACDF,BCEF,ABDE等内容,欢迎下载使用。
初中数学浙教版八年级上册2.8 直角三角形全等的判定备课课件ppt: 这是一份初中数学浙教版八年级上册2.8 直角三角形全等的判定备课课件ppt,共24页。PPT课件主要包含了三角形全等的判定,AAS,方法探究,实验探索,∴BCB´C´,证明一,证明二,证明三,几何语言,连结AB等内容,欢迎下载使用。
初中数学浙教版八年级上册2.8 直角三角形全等的判定一等奖课件ppt: 这是一份初中数学浙教版八年级上册2.8 直角三角形全等的判定一等奖课件ppt,共27页。PPT课件主要包含了情境引入,学习目标,问题引入,∴BCB´C´,几何语言,知识精讲,总结提升,SAS,AAS,针对练习等内容,欢迎下载使用。













