


专题17 解密几何综合压轴题- 2024年中考数学压轴专题重难点突破
展开1.【问题情境】:
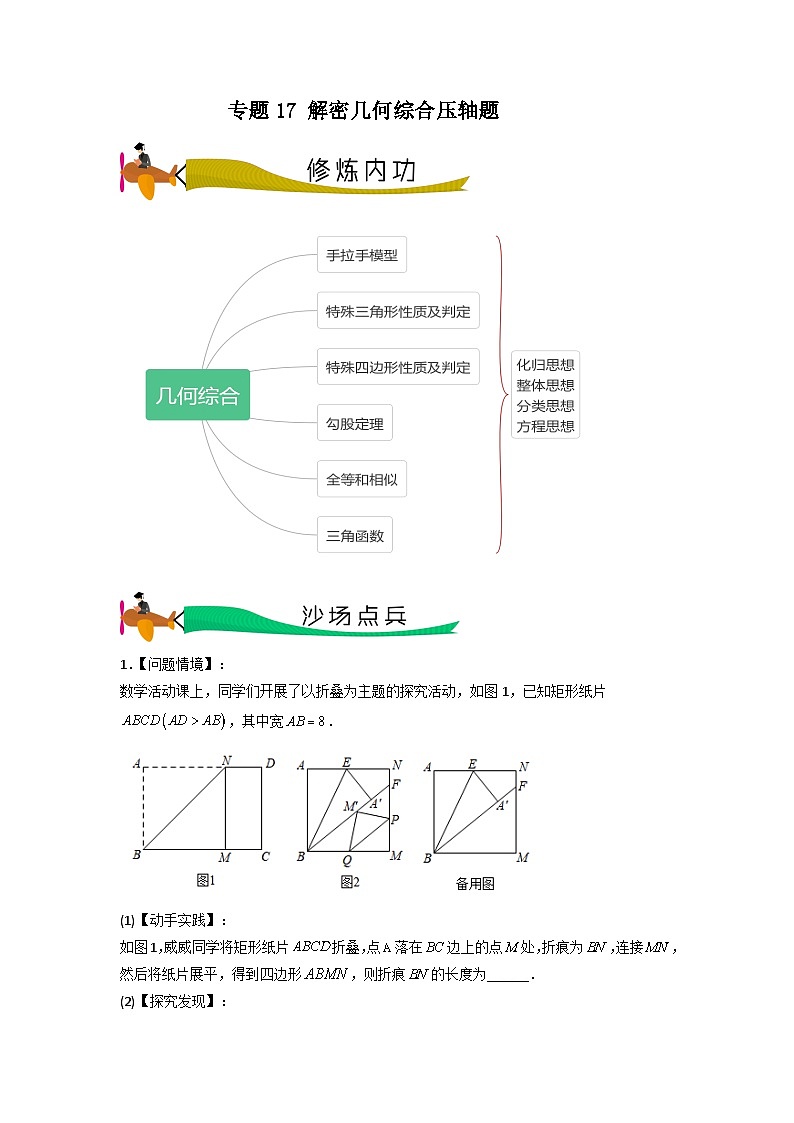
数学活动课上,同学们开展了以折叠为主题的探究活动,如图1,已知矩形纸片,其中宽.
(1)【动手实践】:
如图1,威威同学将矩形纸片折叠,点落在边上的点处,折痕为,连接,然后将纸片展平,得到四边形,则折痕的长度为______.
(2)【探究发现】:
如图2,胜胜同学将图1中的四边形剪下,取边中点,将沿折叠得到,延长交于点.点为边的中点,点是边上一动点,将沿折叠,当点的对应点落在线段上时,求此时的值;
(3)【反思提升】:
明明同学改变图2中点的位置,即点为边上一动点,点仍是边上一动点,按照(2)中方式折叠,使点落在线段上,明明同学不断改变点的位置,发现在某一位置与(2)中的相等,请直接写出此时的长度.
2.综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角:______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ=______°,∠CBQ=______°;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
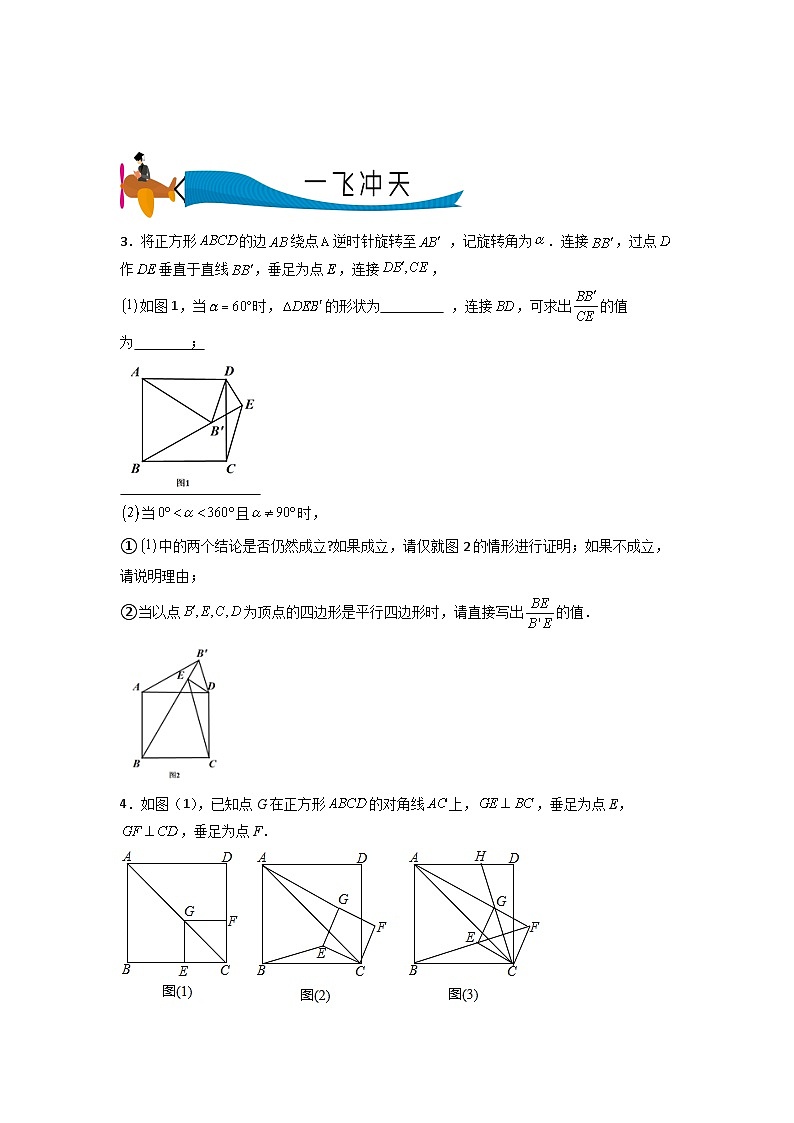
3.将正方形的边绕点逆时针旋转至 ,记旋转角为.连接,过点作垂直于直线,垂足为点,连接,
如图1,当时,的形状为 ,连接,可求出的值为 ;
当且时,
①中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点为顶点的四边形是平行四边形时,请直接写出的值.
4.如图(1),已知点G在正方形的对角线上,,垂足为点E,,垂足为点F.
(1)证明与推断:
①求证:四边形是正方形:
②推断:的值为_____________;
(2)探究与证明:
将正方形绕点C顺时针方向旋转角(),如图(2)所示,试探究线段与之间的数量关系,并说明理由;
(3)拓展与运用:
正方形在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长交于点H.
①求证:.
②若,,则_________________.
5.如图1,在△ABC中,∠ACB=90°,AC=BC=3,点D是直线AB上一动点(点D不与点A,B重合),以CD为边作正方形CDEF,连接AE,AF.
(1)观察猜想
当点D在线段AB上时,线段BD与AF的数量关系是______,∠CAE的度数是______.
(2)探究证明
当点D不在线段AB上时,(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由.
(3)解决问题
当BD时,请直接写出线段AE的长.
6.已知,在△ABC中,AB=AC,点D为边AC上一动点,∠BDE=∠A且DB=DE,连接BE,EC,其中.
问题发现:(1)如图1,若∠A=60°,∠BCE与∠A怎样的数量关系?k的值为多少?直接写出答案.
类比探究:(2)如图2,若,点D在AC的延长线上,∠BCE与∠A有怎样的数量关系?k的值为多少?请说明理由.
拓展应用:(3)如图3,在Rt△ABC中,∠BAC=90°,AB=AC=10,D为AC上一点,以BD为边,在如图所示位置作正方形BDEF,点O为正方形BDEF的对称中心,且OA=,请直接写出DE的长.
7.在四边形中,点为边上一点,点为对角线上的一点,且.
(1)若四边形为正方形;
①如图1,请直接写出与的数量关系;
②将绕点逆时针旋转到图2所示的位置,连接、,猜想与的数量关系并说明理由;
(2)如图3,若四边形为矩形,,其它条件都不变,将绕点逆时针旋转得到△,连接,,请在图3中画出草图,并求出与的数量关系.
8.(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=,请直接写出当点C与点M重合时AC的长.
9.解答题
(1)如图1,和都是等边三角形,连接、,求证,;
[类比探究]
(2)如图2,和都是等腰直角三角形,,连接.求的值.
[拓展提升]
(3)如图3,和都是直角三角形,,.连接,延长交于点F,连接.若恰好等于,请直接写出此时之间的数量关系.
10.如图1,已知矩形中,,O是矩形的中心,过点O作于E,作于F,得矩形BEOF.
(1)线段AE与CF的数量关系是 ,直线AE与CF的位置关系是 ;
(2)固定矩形,将矩形绕点B顺时针旋转到如图2的位置,连接.那么(1)中的结论是否依然成立?请说明理由;
(3)若,当矩形旋转至点O在CF上时(如图3),设OE与BC交于点P,求PC的长.
11.(1)如图1,正方形ABCD的中心为点O,正方形OA′B′C′与正方形ABCD的边长相等.正方形OA′B′C′绕点O旋转,运动过程中两个正方形重叠部分的面积是否发生变化?如果变化,重叠部分的面积如何变化;如果不变,重叠部分的面积与正方形ABCD的面积有何关系?请写出结论并证明.
结论:______________________________________________________
证明:______________________________________________________
(2)如图2,正三角形ABC的中心为点O,正三角形OA′B′与正三角形ABC的边长相等,边OA′经过点B.正三角形OA′B′绕点O顺时针旋转α(0°≤α≤120°),运动过程中两个正三角形重叠部分的面积是否发生变化?如果变化,重叠部分的面积如何变化;如果不变,重叠部分的面积与正三角形ABC的面积有何关系?请写出研究过程.
12.在一次数学探究活动中,李老师设计了一份活动单:
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以为弦的圆弧上(点B、C除外),…….小华同学画出了符合要求的一条圆弧(如图1).
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为___________;
②面积的最大值为_________;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为,请你利用图1证明;
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形的边长,,点P在直线的左侧,且.
①线段长的最小值为_______;
②若,则线段长为________.【提出问题】“其他形状相同的两个图形,在类似上述旋转的过程中,上面发现的结论是否依然成立?”现对正三角形进行研究.
已知线段,使用作图工具作,尝试操作后思考:
(1)这样的点A唯一吗?
(2)点A的位置有什么特征?你有什么感悟?
专题16 创新函数图像综合训练- 2024年中考数学压轴专题重难点突破: 这是一份专题16 创新函数图像综合训练- 2024年中考数学压轴专题重难点突破,文件包含专题16创新函数图像综合训练教师版-2024年中考数学拉分压轴专题重难点突破docx、专题16创新函数图像综合训练学生版-2024年中考数学拉分压轴专题重难点突破docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
专题07 三角形相似综合训练- 2024年中考数学压轴专题重难点突破: 这是一份专题07 三角形相似综合训练- 2024年中考数学压轴专题重难点突破,文件包含专题07三角形相似综合训练教师版-2024年中考数学拉分压轴专题重难点突破docx、专题07三角形相似综合训练学生版-2024年中考数学拉分压轴专题重难点突破docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
专题05 尺规作图与计算- 2024年中考数学压轴专题重难点突破: 这是一份专题05 尺规作图与计算- 2024年中考数学压轴专题重难点突破,文件包含专题05尺规作图与计算教师版-2024年中考数学拉分压轴专题重难点突破docx、专题05尺规作图与计算学生版-2024年中考数学拉分压轴专题重难点突破docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。












