新高考数学圆锥曲线62种题型第三讲 圆的方程（原卷版）

这是一份新高考数学圆锥曲线62种题型第三讲 圆的方程（原卷版），共9页。试卷主要包含了圆的定义和圆的方程，点与圆的位置关系，圆心在任一弦的垂直平分线上等内容，欢迎下载使用。
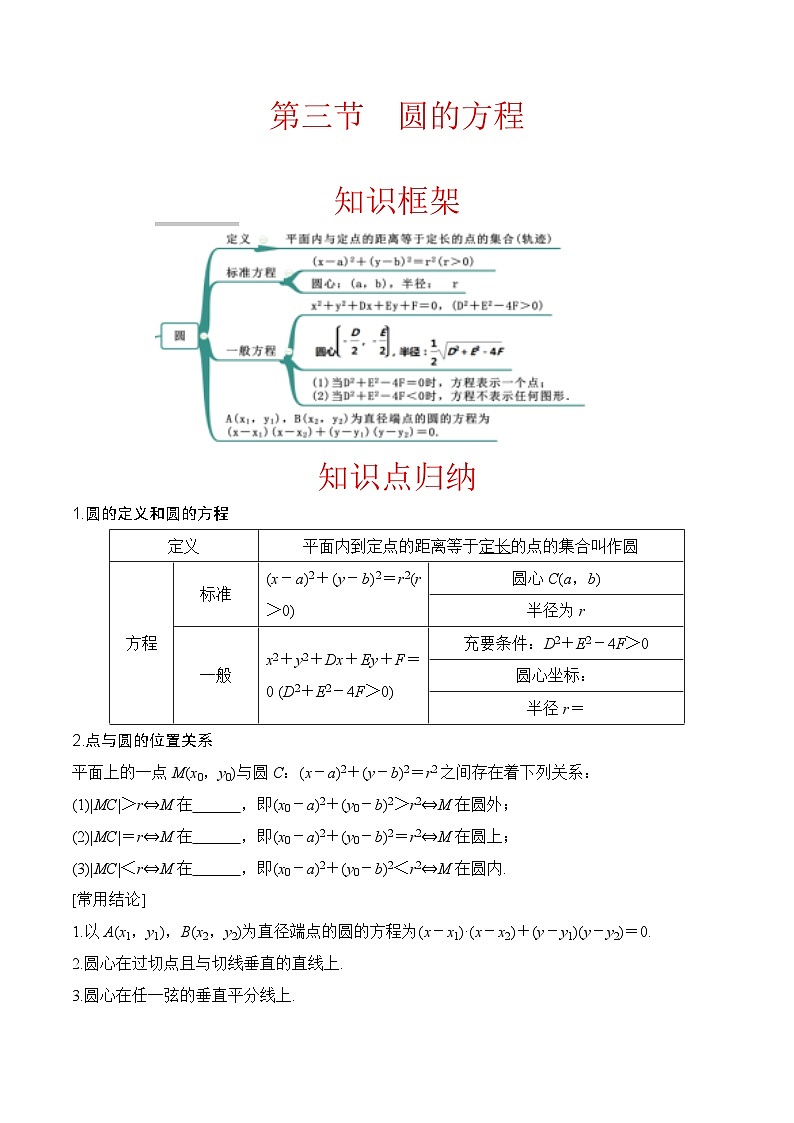
知识框架
知识点归纳
1.圆的定义和圆的方程
2.点与圆的位置关系
平面上的一点M(x0，y0)与圆C：(x－a)2＋(y－b)2＝r2之间存在着下列关系：
(1)|MC|＞r⇔M在 ，即(x0－a)2＋(y0－b)2＞r2⇔M在圆外；
(2)|MC|＝r⇔M在 ，即(x0－a)2＋(y0－b)2＝r2⇔M在圆上；
(3)|MC|＜r⇔M在 ，即(x0－a)2＋(y0－b)2＜r2⇔M在圆内.
[常用结论]
1.以A(x1，y1)，B(x2，y2)为直径端点的圆的方程为(x－x1)·(x－x2)＋(y－y1)(y－y2)＝0.
2.圆心在过切点且与切线垂直的直线上.
3.圆心在任一弦的垂直平分线上.
题型归类
题型一 圆的方程
例1 (1)已知圆M与直线3x－4y＝0及3x－4y＋10＝0都相切，圆心在直线y＝－x－4上，则圆M的方程为________________________.
(2)(2022·全国甲卷)设点M在直线2x＋y－1＝0上，点(3，0)和(0，1)均在⊙M上，则⊙M的方程为________________.
感悟提升 求圆的方程时，应根据条件选用合适的圆的方程.
(1)几何法，通过研究圆的性质进而求出圆的基本量.确定圆的方程时，常用到的圆的三个性质：①圆心在过切点且垂直切线的直线上；②圆心在任一弦的中垂线上；③两圆内切或外切时，切点与两圆圆心三点共线；
(2)代数法，即设出圆的方程，用待定系数法求解.
题型二 与圆有关的最值问题
角度1 利用几何意义求最值
例2 已知点(x，y)在圆(x－2)2＋(y＋3)2＝1上.
(1)求eq \f(y,x)的最大值和最小值；
(2)求x＋y的最大值和最小值；
(3)求eq \r(x2＋y2＋2x－4y＋5)的最大值和最小值.
角度2 利用对称性求最值
例3 已知A(0，2)，点P在直线x＋y＋2＝0上，点Q在圆C：x2＋y2－4x－2y＝0上，则|PA|＋|PQ|的最小值是________.
角度3 建立函数关系求最值
例4 (2023·湘潭质检)设点P(x，y)是圆：x2＋(y－3)2＝1上的动点，定点A(2，0)，B(－2，0)，则eq \(PA,\s\up6(→))·eq \(PB,\s\up6(→))的最大值为________.
感悟提升 与圆有关的最值问题的求解方法
(1)借助几何性质求最值：形如μ＝eq \f(y－b,x－a)，t＝ax＋by，(x－a)2＋(y－b)2形式的最值问题.
(2)建立函数关系式求最值：列出关于所求目标式子的函数关系式，然后根据关系式的特征选用配方法、判别式法、基本不等式法等求最值.
(3)求解形如|PM|＋|PN|且与圆C有关的折线段的最值问题的基本思路：
①“动化定”，把与圆上动点的距离转化为与圆心的距离；②“曲化直”，即将折线段之和转化为同一直线上的两线段之和，一般要通过对称性解决.
题型三 与圆有关的轨迹问题
例5 如图，等腰梯形ABCD的底边AB和CD的长分别为6和2eq \r(6)，高为3.
(1)求这个等腰梯形的外接圆E的方程；
(2)若线段MN的端点N的坐标为(5，2)，端点M在圆E上运动，求线段MN的中点P的轨迹方程.
感悟提升 求与圆有关的轨迹问题时，根据题设条件的不同常采用以下方法：
(1)直接法，直接根据题目提供的条件列出方程；
(2)定义法，根据圆、直线等定义列方程；
(3)几何法，利用圆的几何性质列方程；
(4)代入法，找到要求点与已知点的关系，代入已知点满足的关系式.
课时训练
一、单选题
1．圆C：关于直线对称的圆的方程是（ ）
A．B．
C．D．
2．方程表示圆，则实数的取值范围为（ ）
A．B．
C．D．
3．圆关于原点对称的圆的方程为（ ）
A．B．
C．D．
4．已知，两点，以线段AB为直径的圆的标准方程是（ ）
A．B．
C．D．
5．已知圆的圆心在直线上，且圆与轴相切，则圆的方程为
A．B．
C．D．
6．已知点，，点是圆上的动点，点是圆上的动点，则的最小值为（ ）
A．5B．C．D．
二、多选题
7．已知圆的一般方程为，则下列说法正确的是（ ）
A．圆的圆心为
B．圆的半径为5
C．点不在圆上
D．圆关于对称
8．已知三角形的三个顶点分别为，，，则（ ）
A．三角形OMN外接圆的方程为
B．三角形OMN外接圆的半径长为5
C．三角形OMN外接圆的圆心坐标
D．大于三角形OMN外接圆的半径
三、填空题
9．已知点，，则以线段为直径的圆的标准方程为______.
10．方程表示一个圆，且过点有两条直线与该圆相切，则实数的取值范围是__________.
11．已知圆，，是圆上两点，点且，则线段中点的轨迹方程是______.
12．已知圆：，在圆内随机取一点，直线交圆于，两点（为坐标原点），则的概率为_____．
四、解答题
13．求过点，且圆心在直线上的圆的方程.
14．已知圆经过点，，且圆与轴相切．
(1)求圆的一般方程；
(2)设是圆上的动点，求线段的中点的轨迹方程．
15．若圆的内接矩形的周长最大值为．
(1)求圆O的方程；
(2)若过点的直线与圆O交于A，B两点，如图所示，且直线的斜率，求的取值范围．
16．在以O为原点的直角坐标系中，点为△OAB的直角顶点，已知，且点B的纵坐标大于零.
(1)求的坐标；
(2)设点，求以OC为直径的圆M关于直线OB对称的圆的方程.
定义
平面内到定点的距离等于定长的点的集合叫作圆
方程
标准
(x－a)2＋(y－b)2＝r2(r＞0)
圆心C(a，b)
半径为r
一般
x2＋y2＋Dx＋Ey＋F＝0 (D2＋E2－4F＞0)
充要条件：D2＋E2－4F＞0
圆心坐标：
半径r＝