新高考数学一轮复习《双曲线》学案 基础班（2份打包，原卷版+教师版）

这是一份新高考数学一轮复习《双曲线》学案 基础班（2份打包，原卷版+教师版），文件包含新高考数学一轮复习《双曲线》学案基础班原卷版doc、新高考数学一轮复习《双曲线》学案基础班教师版doc等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。
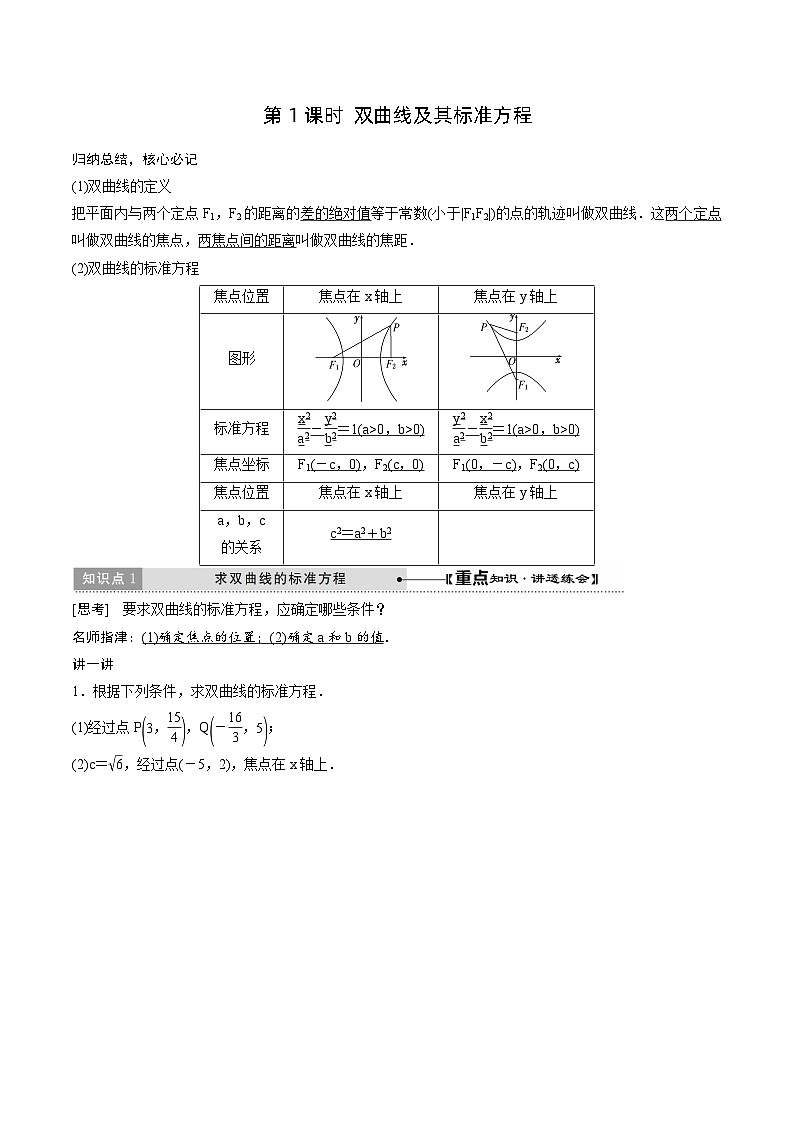
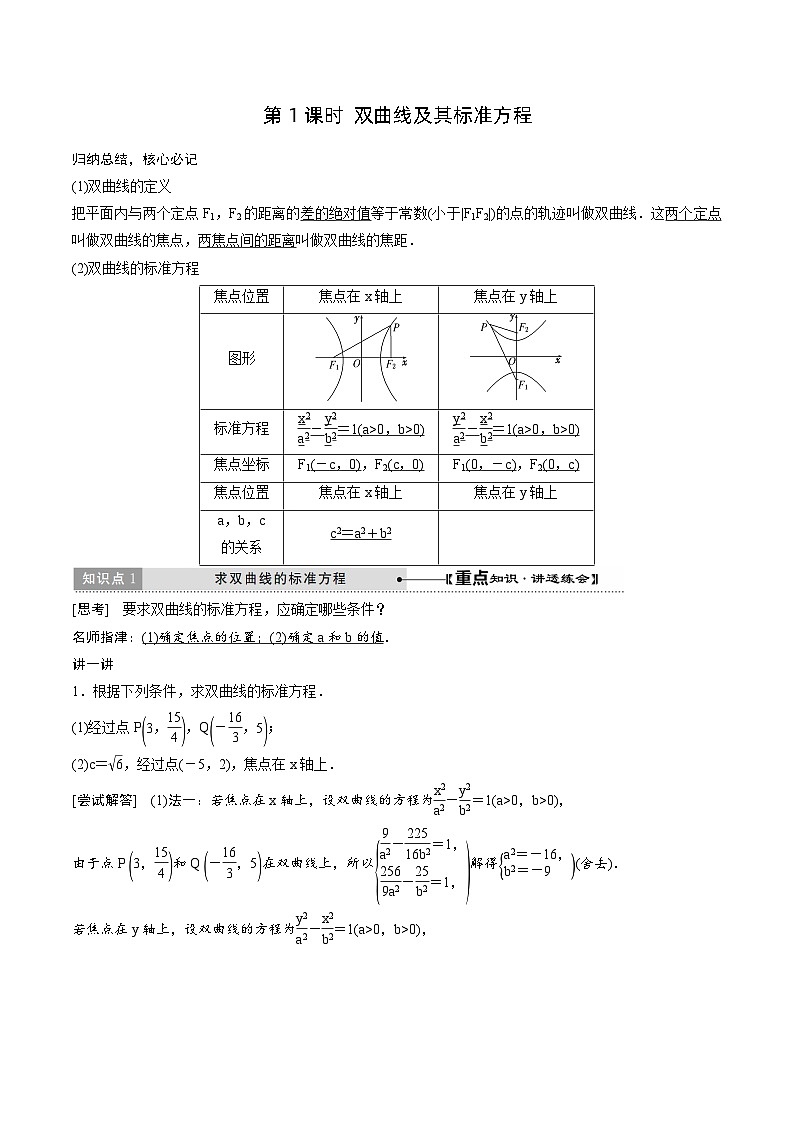
(1)双曲线的定义
把平面内与两个定点F1，F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．
(2)双曲线的标准方程
[思考] 要求双曲线的标准方程，应确定哪些条件？
名师指津：(1)确定焦点的位置；(2)确定a和b的值．
讲一讲
1．根据下列条件，求双曲线的标准方程．
(1)经过点Peq \b\lc\(\rc\)(\a\vs4\al\c1(3，\f(15,4)))，Qeq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(16,3)，5))；
(2)c＝eq \r(6)，经过点(－5，2)，焦点在x轴上．
[尝试解答] (1)法一：若焦点在x轴上，设双曲线的方程为eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)，
由于点Peq \b\lc\(\rc\)(\a\vs4\al\c1(3，\f(15,4)))和Qeq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(16,3)，5))在双曲线上，所以eq \b\lc\{(\a\vs4\al\c1(\f(9,a2)－\f(225,16b2)＝1，,\f(256,9a2)－\f(25,b2)＝1，))解得eq \b\lc\{(\a\vs4\al\c1(a2＝－16，,b2＝－9))(舍去)．
若焦点在y轴上，设双曲线的方程为eq \f(y2,a2)－eq \f(x2,b2)＝1(a>0，b>0)，
将P、Q两点坐标代入可得eq \b\lc\{(\a\vs4\al\c1(\f(225,16a2)－\f(9,b2)＝1，,\f(25,a2)－\f(256,9b2)＝1，))解得eq \b\lc\{(\a\vs4\al\c1(a2＝9，,b2＝16，))所以双曲线的标准方程为eq \f(y2, 9)－eq \f(x2,16)＝1.
法二：设双曲线方程为eq \f(x2,m)＋eq \f(y2,n)＝1(mn0，b>0)．
依题设有eq \b\lc\{(\a\vs4\al\c1(a2＋b2＝6，,\f(25,a2)－\f(4,b2)＝1，))解得eq \b\lc\{(\a\vs4\al\c1(a2＝5，,b2＝1，))∴所求双曲线的标准方程为eq \f(x2,5)－y2＝1.
法二：∵焦点在x轴上，c＝eq \r(6)，∴设所求双曲线方程为eq \f(x2,λ)－eq \f(y2,6－λ)＝1(其中00，,00)，
∴双曲线的渐近线方程为y＝±eq \f(a,b)x，∴所求双曲线的渐近线方程为y＝±eq \f(3,4)x.
5．已知点(2,3)在双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)上，C的焦距为4，则它的离心率为________．
答案 2
解析 由题意知eq \f(4,a2)－eq \f(9,b2)＝1，c2＝a2＋b2＝4，解得a＝1，所以e＝eq \f(c,a)＝2.
课时达标训练
[即时达标对点练]
题组1 根据双曲线的标准方程研究几何性质
1．双曲线mx2＋y2＝1的虚轴长是实轴长的2倍，则m的值为( )
A．－eq \f(1,4) B．－4 C．4 D.eq \f(1,4)
解析：选A 由双曲线方程mx2＋y2＝1，知m0，b>0)的离心率为eq \f(\r(5),2)，则C的渐近线方程为( )
A．y＝±eq \f(1,4)x B．y＝±eq \f(1,3)x C．y＝±eq \f(1,2)x D．y＝±x
解析：选C 因为双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1的焦点在x轴上，所以双曲线的渐近线方程为
y＝±eq \f(b,a)x.又离心率为e＝eq \f(c,a)＝eq \f(\r(a2＋b2),a)＝eq \r(1＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(b,a)))\s\up12(2))＝eq \f(\r(5),2)，所以eq \f(b,a)＝eq \f(1,2)，所以双曲线的渐近线方程为y＝±eq \f(1,2)x.
7．双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(00)的离心率为eq \f(\r(5),2)，则双曲线C的渐近线方程为( )
A．y＝±eq \f(1,4)x B．y＝±eq \f(1,3)x C．y＝±eq \f(1,2)x D．y＝±x
答案 C
解析 已知双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的离心率为eq \f(\r(5),2)，故有eq \f(a2＋b2,a2)＝eq \f(5,4)，所以eq \f(b2,a2)＝eq \f(1,4)，解得eq \f(b,a)＝eq \f(1,2).
故双曲线C的渐近线方程为y＝±eq \f(1,2)x，故选C.
6．若一双曲线与椭圆4x2＋y2＝64有公共的焦点，且它们的离心率互为倒数，则该双曲线的方程为________．
答案 y2－3x2＝36
解析 椭圆4x2＋y2＝64可变形为eq \f(x2,16)＋eq \f(y2,64)＝1，a2＝64，c2＝64－16＝48，
∴焦点为(0,4eq \r(3))，(0，－4eq \r(3))，离心率e＝eq \f(\r(3),2)，则双曲线的焦点在y轴上，c′＝4eq \r(3)，e′＝eq \f(2,\r(3))，
从而a′＝6，b′2＝12，故所求双曲线的方程为y2－3x2＝36.
7．求适合下列条件的双曲线的标准方程．
(1)两顶点间的距离是6，两焦点所连线段被两顶点和中心四等分；
(2)渐近线方程为2x±3y＝0，且两顶点间的距离是6.
解 (1)由两顶点间的距离是6，得2a＝6，即a＝3.
由两焦点所连线段被两顶点和中心四等分可得2c＝4a＝12，即c＝6，
于是有b2＝c2－a2＝62－32＝27.
由于焦点所在的坐标轴不确定，故所求双曲线的标准方程为eq \f(x2,9)－eq \f(y2,27)＝1或eq \f(y2,9)－eq \f(x2,27)＝1.
(2)设双曲线方程为4x2－9y2＝λ(λ≠0)，即eq \f(x2,\f(λ,4))－eq \f(y2,\f(λ,9))＝1(λ≠0)，由题意得a＝3.
当λ>0时，eq \f(λ,4)＝9，λ＝36，双曲线方程为eq \f(x2,9)－eq \f(y2,4)＝1；
当λ0，b>0)
eq \f(y2,a2)－eq \f(x2,b2)＝1(a>0，b>0)
焦点坐标
F1(－c，0)，F2(c，0)
F1(0，－c)，F2(0，c)
焦点位置
焦点在x轴上
焦点在y轴上
a，b，c
的关系
c2＝a2＋b2
标准方程
eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)
eq \f(y2,a2)－eq \f(x2,b2)＝1(a>0，b>0)
图形
性
质
焦点
(±c，0)
(0，±c)
焦距
2c
2c
范围
x≥a或x≤－a，y∈R
y≥a或y≤－a，x∈R
对称性
对称轴：x轴和y轴，中心：(0，0)
顶点
(±a，0)
(0，±a)
轴长
实轴长＝2a，虚轴长＝2b
离心率
e＝eq \f(c,a)∈(1，＋∞)
渐近线
y＝±eq \f(b,a)x
y＝±eq \f(a,b)x