


- 期末仿真测试卷(扬州专用)-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题01 易错题精选01之旋转与中心对称专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题03 易错题精选03之矩形、菱形与中位线专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题04 易错题精选04之最值专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 1 次下载
- 专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
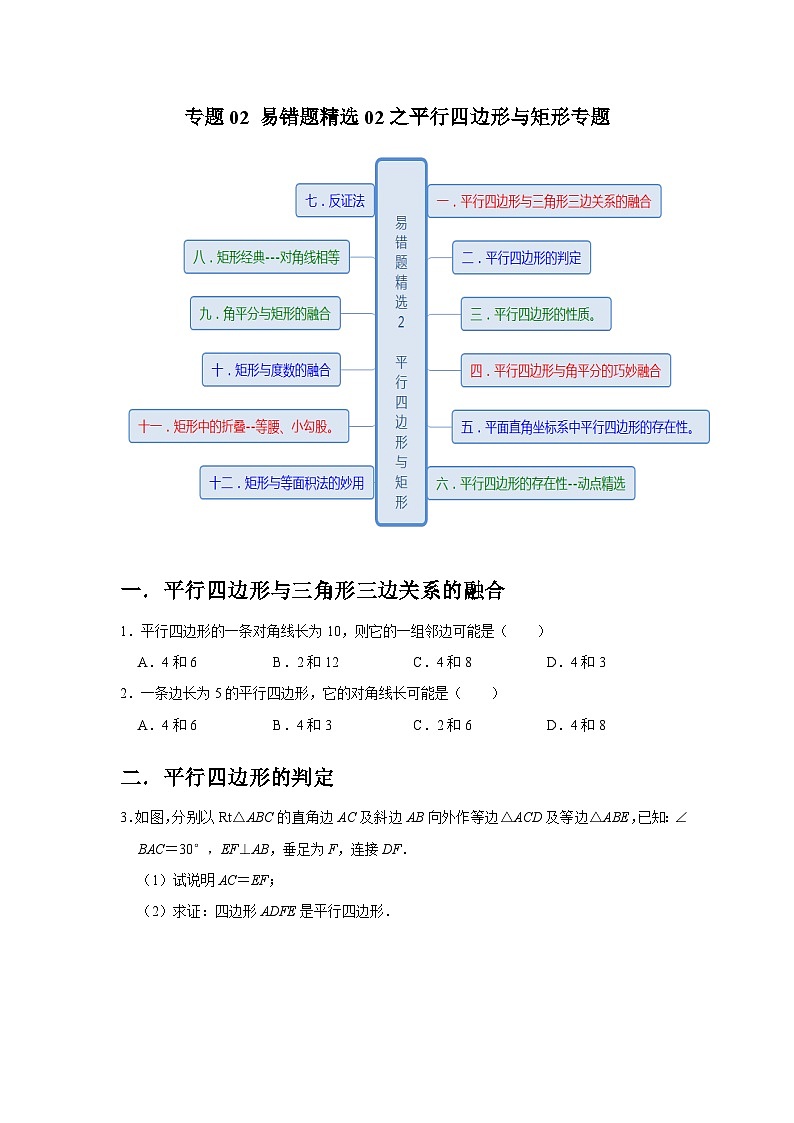
专题02 易错题精选02之平行四边形与矩形专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版)
展开一.平行四边形与三角形三边关系的融合
1.平行四边形的一条对角线长为10,则它的一组邻边可能是( )
A.4和6B.2和12C.4和8D.4和3
试题分析:平行四边形的一条对角线正好把平行四边形分成两个三角形,平行四边形的一组邻边长正好是三角形的两边,平行四边形的对角线正好为三角形的第三边,所以要讨论第三边与两边之和的关系.
答案详解:解:由题意得:平行四边形的一组邻边长正好是三角形的两边,平行四边形的对角线正好为三角形的第三边,
∵平行四边形的一条对角线长为10,
∴它的一组邻边必须:满足之和大于10,差小于10,
∴它的一组邻边可能是:4和8,
所以选:C.
2.一条边长为5的平行四边形,它的对角线长可能是( )
A.4和6B.4和3C.2和6D.4和8
试题分析:根据平行四边形的性质中,两条对角线的一半和一边构成三角形,利用三角形三边关系判断可知.
答案详解:解:A、对角线一半分别是2和3,2+3=5,故不能构成三角形,故本选项不符合题意;
B、对角线一半分别是2和1.5,2+1.5=3.5<5,故不能构成三角形,故本选项不符合题意;
C、对角线一半分别是1和3,1+3<5,故不能构成三角形,故本选项不符合题意;
D、对角线一半分别是2和4,符合三角形的三边关系,能构成三角形,故本选项符合题意.
所以选:D.
二.平行四边形的判定
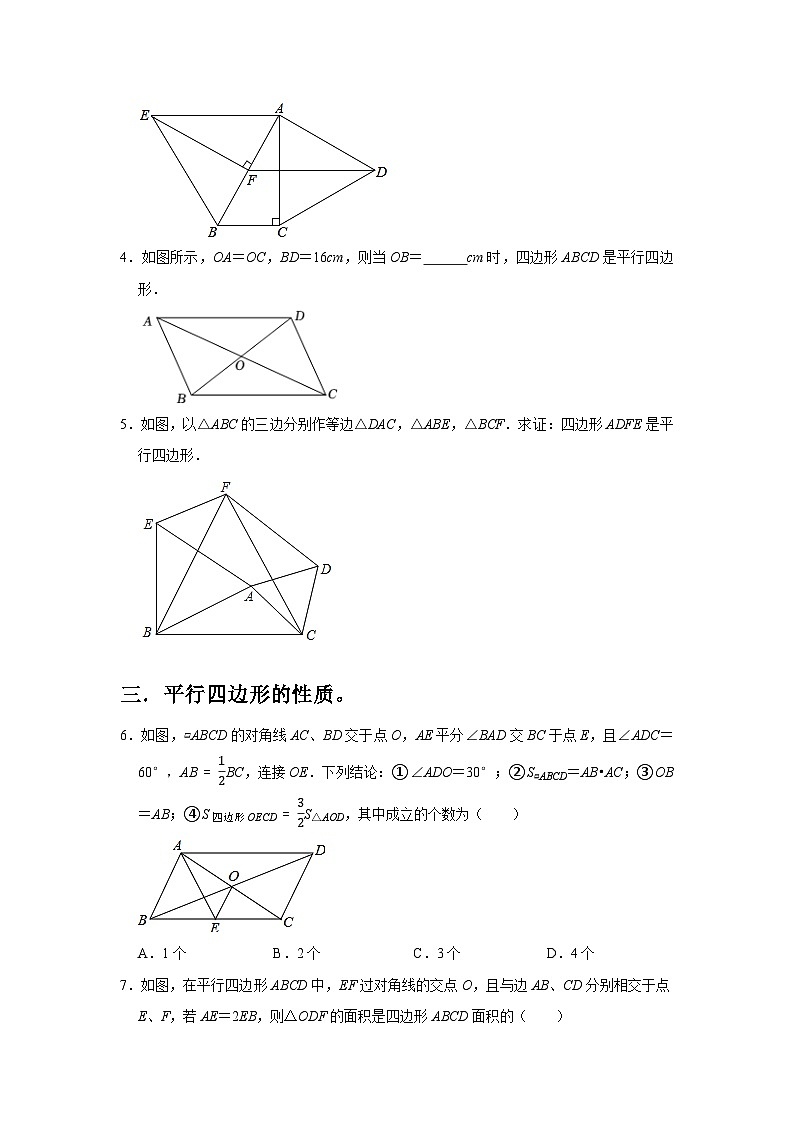
3.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
试题分析:(1)首先由Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又由△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后证得△AFE≌△BCA,继而证得结论;
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
答案详解:证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
AF=BCAE=BA,
∴Rt△AFE≌Rt△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
4.如图所示,OA=OC,BD=16cm,则当OB= 8 cm时,四边形ABCD是平行四边形.
试题分析:求出OB=OD,再由平行四边形的判定即可得出结论.
答案详解:解:当OB=8cm时,四边形ABCD是平行四边形.理由如下:
∵BD=16cm,OB=8cm,
∴OD=BD﹣OB=8(cm),
∴OB=OD,
∵OA=OC,
∴四边形ABCD是平行四边形,
所以答案是:8.
5.如图,以△ABC的三边分别作等边△DAC,△ABE,△BCF.求证:四边形ADFE是平行四边形.
试题分析:由△ABE与△BCF都为等边三角形,利用等边三角形的性质得到两对边相等,∠ABE=∠CBF=60°,利用等式的性质得到夹角相等,利用SAS得到△EBF≌△ABC;利用全等三角形对应边相等得到EF=AC,再由三角形ADC为等边三角形得到三边相等,等量代换得到EF=AD,同理可得AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形.
答案详解:证明:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,
即∠CBA=∠FBE,
在△EBF和△ABC中,
EB=AB∠FBE=∠CBABF=BC,
∴△EBF≌△ABC(SAS);
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴AB=AE=DF,
∴四边形AEFD是平行四边形.
三.平行四边形的性质。
6.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=12BC,连接OE.下列结论:①∠ADO=30°;②S▱ABCD=AB•AC;③OB=AB;④S四边形OECD=32S△AOD,其中成立的个数为( )
A.1个B.2个C.3个D.4个
试题分析:结合平行四边形的性质可证明△ABE为等边三角形,由AB=12BC,可得EC=AE=BE,由三角形中位线定理可判定③,证明∠BAC=90°,可判定①;由平行四边形的面积公式可判定②;利用三角形中线的性质结合三角形的面积可求解判定④.
答案详解:解:∵四边形ABCD为平行四边形,∠ADC=60°,
∴AD∥BC,∠ABC=∠ADC=60°,OB=OD,AO=CO,
∴∠DAE=∠AEB,∠BAD=∠BCD=120°,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB
∴△ABE为等边三角形,
∴∠BAE=∠AEB=60°,AB=BE=AE,
∵AB=12BC,
∴EC=AE=BE,
又∵AO=CO,
∴∠EAC=∠ECA=30°,OE=12AB,
∴∠CAD=30°,OB≠OC,
∴∠OBC≠∠OCB≠30°,
∴∠ADO≠30°,故①错误;
∵∠BAD=120°,∠CAD=30°,
∴∠BAC=90°,
∴BO>AB,∴故③错误;
∴S▱ABCD=AB•AC=AC•CD,故②正确;
∵∠BAC=90°,BC=2AB,
∴E是BC的中点,
∴S△BEO:S△BCD=1:4,
∴S四边形OECD:S△BCD=3:4,
∴S四边形OECD:S▱ABCD=3:8,
∵S△AOD:S▱ABCD=1:4,
∴S四边形OECD=32S△AOD,故④正确.
所以选:B.
7.如图,在平行四边形ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F,若AE=2EB,则△ODF的面积是四边形ABCD面积的( )
A.112B.16C.14D.18
试题分析:根据AE=2EB可得S△OBE=13S△AOB,由平行四边形的性质可得S△AOB=14S△D平行四边形ABC,即可得S△OBE=112S平行四边形ABC,通过证明△ODF≌△OBE可得S△ODF=S△OBE,进而可求解.
答案详解:解:∵AE=2EB,
∴EB=13AB,
∴S△OBE=13S△AOB,
∵四边形ABCD为平行四边形,
∴S△AOB=14S△D平行四边形ABC,AB∥CD,OD=OF,
∴S△OBE=112S平行四边形ABC,∠ODF=∠OBE,∠OFD=∠OEB,
在△ODF和△OBE中,
∠OFD=∠OEB∠ODF=∠OBEOD=OF,
∴△ODF≌△OBE(AAS),
∴S△ODF=S△OBE,
∴S△ODF=112S平行四边形ABCD,
所以选:A.
四.平行四边形与角平分的巧妙融合
8.如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF.
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
试题分析:①利用平行四边形的性质,判定△ABF≌△DEF,即可得出AB=DE;
②利用角平分线以及平行线的性质,即可得到AF=AB=3,进而得出BC=AD=6,CD=AB=3,依据△ABF≌△DEF,可得DE=AB=3,EF=BF=5,进而得到△BCE的周长.
答案详解:解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠A=∠FDE,∠ABF=∠E,
∵AF=DF,
∴△ABF≌△DEF,
∴AB=DE;
②∵BE平分∠ABC,
∴∠ABF=∠CBF,
∵AD∥BC,
∴∠CBF=∠AFB,
∴∠ABF=∠AFB,
∴AF=AB=3,
∴AD=2AF=6
∵四边形ABCD是平行四边形,
∴BC=AD=6,CD=AB=3,
∵△ABF≌△DEF,
∴DE=AB=3,EF=BF=5,
∴CE=6,BE=EF+BF=10,
∴△BCE的周长=BC+CE+BE=10+6+6=22.
9.如图,在平行四边形ABCD中,∠ABC的角平分线交AD于点E,∠BCD的角平分线交AD于点F,若AB=7,BC=10,则DE的长为( )
A.3B.4C.5D.6
试题分析:由平行四边形的性质得AD=BC=10,AD∥BC,再证∠AEB=∠ABE,得AE=AB=7,即可得出结论.
答案详解:解:∵四边形ABCD是平行四边形,
∴AD=BC=10,AD∥BC,
∴∠AEB=∠CBE,
又∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AE=AB=7,
∴DE=AD﹣AE=10﹣7=3,
所以选:A.
10.如图,已知平行四边形ABCD中,3AB=2BC,点O是∠BAD和∠CBA的角平分线的交点,过点O作EF∥AB,分别交AD、BC于E、F两点,连接OD、OC.则下列结论:①AO⊥BO;②点O是EF的中点;③DE=2AE;④S△OCD=4S△OAE,其中正确的有( )
A.1个B.2个C.3个D.4个
试题分析:利用平行四边形的性质得到AD∥BC,AB∥CD,AB=CD,AD=BC,利用平行线的性质和角平分线的定义计算出∠OAB+∠OBA=90°,则∠AOB=90°,于是可对①进行判断;利用平行线的性质证明∠EAO=∠AOE,∠OBF=∠BOF得到AE=OE,BF=OF,再证明四边形ABFE为平行四边形得到AE=BF,所以OE=OF,则可对②进行判断;设AB=2x,BC=3x,则EF=2x,AD=3x,EA=OE=x,DE=2x,则可对③进行判断;利用三角形面积公式和平行四边形的面积公式得到S平行四边形ABFE=12S平行四边形FEDC,S△OAB=12S平行四边形ABFE,S△OCD=12S平行四边形FEDC,S△OAB=12S△OCD,S△AOE=12S△OAB,所以S△AOE=14S△OCD,从而可对④进行判断.
答案详解:解:∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,AB=CD,AD=BC,
∴∠BAD+∠ABC=180°,
∵点O是∠BAD和∠CBA的角平分线的交点,
∴∠OAB=12∠BAD,∠OBA=12∠ABC,
∴∠OAB+∠OBA=12(∠BAD+∠ABC)=12×180°=90°,
∴∠AOB=90°,
∴AO⊥BO,所以①正确;
∵EF∥AB,
∴∠OAE=∠AOE,∠OBA=∠BOF,
∴∠EAO=∠AOE,∠OBF=∠BOF,
∴AE=OE,BF=OF,
∵AE∥BF,AB∥EF,
∴四边形ABFE为平行四边形,
∴AE=BF,
∴OE=OF,即O点为EF的中点,所以②正确;
∵3AB=2BC,
∴设AB=2x,BC=3x,
∴EF=2x,AD=3x,
∴EA=OE=12EF=x,
∴DE=AD﹣AE=3x﹣x=2x,
∴DE=2AE,所以③正确;
而AB=CD,
∴S平行四边形ABFE=12S平行四边形FEDC,
∵S△OAB=12S平行四边形ABFE,S△OCD=12S平行四边形FEDC,
∴S△OAB=12S△OCD,
∵OE=OF,
∴S△AOE=S△BOF,
∴S△AOE=12S△OAB,
∴S△AOE=14S△OCD,所以④正确.
所以选:D.
五.平面直角坐标系中平行四边形的存在性。
11.在平面直角坐标系中,已知平行四边形的三个顶点的坐标分别为(0,0),(3,0),(5,3),则第四个顶点的坐标为 (8,3),(2,3),(﹣2,﹣3) .
试题分析:分三种情况讨论,利用平行四边形的性质可求解.
答案详解:解:设O(0,0),A(3,0),B(5,3),
以AB为平行四边形的对角线,则第四个顶点的坐标为(8,3);
以OB为平行四边形的对角线,则第四个顶点的坐标为(2,3);
以AO为平行四边形的对角线,则第四个顶点的坐标为(﹣2,﹣3).
所以答案是:(8,3),(2,3),(﹣2,﹣3).
12.在平面直角坐标系中,已知点A(0,0)、点B(0,﹣5)、点C(﹣2,﹣2),则以A、B、C、D为顶点的四边形为平行四边形的第四个顶点D不可能在( )
A.第一象限B.第二象限C.第三象限D.第四象限
试题分析:可用点平移的问题来解决,从A到B横坐标不变,纵坐标变化5,那么从C到点D,横坐标不变,纵坐标也变化5,为(﹣2,﹣7)或(﹣2,3)分别在第三象限或第二象限;从C到A横坐标加2,纵坐标加2,那么从B到D也应如此,应为(2,﹣3),在第四象限,即可得出结果.
答案详解:解:根据平移的性质分两种情况:
①从A到B横坐标不变,纵坐标变化5,那么从C到点D,横坐标不变,纵坐标也变化5,则D点为(﹣2,﹣7)或(﹣2,3),即分别在第三象限或第二象限.
②从C到A横坐标加2,纵坐标加2,那么从B到D也应如此,应为(2,﹣3),即在第四象限.
所以选:A.
13.在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,2)三点,现以A,B,C,D为顶点作平行四边形,则第四个顶点D的坐标是 (﹣1.2)或(﹣3,﹣2)或(7,2) .
试题分析:首先画出坐标系,再分别以AC、AB、BC为对角线通过线段平移作出平行四边形,进而可得D点坐标.
答案详解:解:如图,
当以AC为对角线,此时D(﹣1,2);
当以AB为对角线时,此时D′(﹣3,﹣2);
当以BC为对角线时,此时点D″(7,2).
则第四个顶点D的坐标是(﹣1.2)或(﹣3,﹣2)或(7,2).
所以答案是:(﹣1.2)或(﹣3,﹣2)或(7,2).
14.如图,点A(1,2),点B(2,0).求:
(1)求OA和AB的解析式;
(2)在坐标平面内存在一点C,使得以O、A、C、B为顶点的四边形为平行四边形,直接写出点C的坐标.
试题分析:(1)由两点之间距离公式可求AB的长,由待定系数法可求直线AB的解析式;
(2)分三种情况讨论,由平行四边形的性质可求解.
答案详解:解:(1)∵点A(1,2),点B(2,0),
∴AB=(1−2)2+(2−0)2=5,
设直线AB的解析式为y=kx+b,
2=k+b0=2k+b,
解得:k=−2b=4,
∴直线AB的解析式为y=﹣2x+4;
(2)设点C(x,y),
当OA,OB为边时,∵四边形OACB是平行四边形,
∴AB与OC互相平分,
∴1+22=0+x2,2+02=0+y2,
∴x=3,y=2,
∴点C(3,2);
当OB、AB为边时,∵四边形ABOC是平行四边形,
∴OA与BC互相平分,
∴0+12=2+x2,0+22=0+y2
∴x=﹣1,y=2,
∴点C(﹣1,2);
当AO、AB为边时,∵四边形OABC是平行四边形,
∴AC与OB互相平分,
∴1+x2=0+22,2+y2=0+02,
∴x=1,y=﹣2,
∴点C(1,﹣2),
综上所述:点C坐标为:(3,2)或(﹣1,2)或(1,﹣2).
六.平行四边形的存在性--动点精选
15.如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP= t ;DP= 12﹣t ;BQ= 15﹣2t ;CQ= 2t .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
试题分析:(1)根据速度、路程以及时间的关系和线段之间的数量关系,即可求出AP,DP,BQ,CQ的长
(2)当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
(3)当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
答案详解:解:(1)t,12﹣t,15﹣2t,2t
(2)根据题意有AP=tcm,CQ=2tcm,PD=(12﹣t)cm,BQ=(15﹣2t)cm.
∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴t=5s时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=(12﹣t)cm,
如图1,∵AD∥BC,即PD∥CQ,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
16.如图,等边△ABC的边长为8,动点M从点B出发,沿B→A→C→B的方向以每秒3个单位长度的速度运动,动点N从点C出发,沿C→A→B﹣C的方向以每秒2个单位长度的速度运动.
(1)若动点M、N同时出发,经过几秒第一次相遇?
(2)若动点M、N同时出发,且其中一点到达终点时,另一点即停止运动.在△ABC的边上是否存在一点D,使得以点A、M、N、D为顶点的四边形为平行四边形?若存在,求此时运动的时间t及点D的具体位置;若不存在,请说明理由.
试题分析:(1)设经过t秒钟两点第一次相遇,然后根据点M运动的路程+点N运动的路程=AB+CA列方程求解即可;
(2)首先根据题意画出图形:如图②,当0≤t≤83时,MC+BN=AN+BN=8;当83<t≤4时,此时A、M、N三点在同一直线上,不能构成平行四边形;4<t≤163时,MB+NC=AN+CN=8;当163<t≤8时,△BNM为等边三角形,由BN=BM可求得t的值.
答案详解:解:(1)
第一次相遇时间=8+83+2=165(秒);
答:若动点M、N同时出发,经过165秒钟两点第一次相遇;
(2)如图2,当点M在线段AB上,点N在AC上时:
∵四边形ANDM为平行四边形,
DM=AN DM∥AN
∵△ABC为等边三角形,
△BMD和△NCD是等边三角形,
∴BM+CN=CN+AN=8,
∴2t+3t=8,
∴t=85,
此时BD=245;
如图3,当点M在线段AC上,点N在AB上时:
同理△BND和△MCD是等边三角形,
AM=3t﹣8,
AN=2t﹣8,
∴AM+AN=AC=8,
3t﹣8+2t﹣8=8,
t=245,
此时BD=325.
如图4,当点M在线段BC上,点N在AB上时,
同理△BMN和△MCD是等边三角形
CM=3t﹣16
AN=2t﹣8
∴CM=AN.
3t﹣16=2t﹣8.
t=8>7.5(不合题意,舍去).
综上所述:运动了85或245时,A、M、N、D四点能够成平行四边形,此时点D在BC上,且BD=245或325.
17.如图,在△ABC中,AB=AC=20cm,BD⊥AC于点D,且BD=16cm.点M从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为1cm/s,过点P的直线PQ∥AC,交BC于点Q,连接PM,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD= 12 cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形是平行四边形?
试题分析:(1)由勾股定理求出AD即可;
(2)由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB,再由等腰三角形的判定定理即可得出结论;
(3)分两种情况:①当点M在点D的上方时,PQ=BP=tcm,AM=4tcm,AD=12cm,得出MD=AD﹣AM=(12﹣4t)cm,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可;
②当点M在点D的下方时,PQ=BP=tcm,AM=4tcm,AD=12cm,得出MD=AM﹣AD=(4t﹣12)cm,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可.
答案详解:(1)解:在Rt△ABD中,由勾股定理得:AD=AB2−BD2=202−162=12(cm),
所以答案是:12;
(2)证明:如图1所示:
∵AB=AC,
∴∠ABC=∠C,即∠PBQ=∠C,
∵PQ∥AC,
∴∠PQB=∠C,
∴∠PBQ=∠PQB,
∴PB=PQ;
(3)解:分两种情况:
①当点M在点D的上方时,如图2所示:
由题意得:PQ=BP=tcm,AM=4tcm,AD=12cm,
∴MD=AD﹣AM=(12﹣4t)cm,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即当t=(12﹣4t)cm时,四边形PQDM是平行四边形,
解得:t=125(s);
②当点M在点D的下方时,如图3所示:
根据题意得:PQ=BP=tcm,AM=4tcm,AD=12cm,
∴MD=AM﹣AD=(4t﹣12)cm,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即当t=(4t﹣12)cm时,四边形PQDM是平行四边形,
解得:t=4(s);
综上所述,当t=125s或t=4s时,以P、Q、D、M为顶点的四边形是平行四边形.
18.如图,长方形ABCD中,AB=4cm,BC=9cm,点E、F分别在AD、BC上,且BF=DE=3cm,连接AF、CE.
(1)求证:四边形AFCE是平行四边形;
(2)动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中:已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
试题分析:(1)首先根据矩形的性质可得AD=BC,AD∥CB,再由BF=DE可得AE=FC,根据一组对边平行且相等的四边形是平行四边形可证得结论;
(2)首先分析出只有当P点在BF上、Q点在ED上时,才能构成平行四边形,然后利用勾股定理计算出AF长,再表示出t秒后PC、AQ的长,然后可得方程5t﹣5+6=13﹣4t,再解即可.
答案详解:(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥CB,
∵BF=DE,
∴AD﹣DE=CB﹣BF,
∴AE=FC,
∴四边形AFCE是平行四边形;
(2)当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形(如图),
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵AB=4cm,BF=3cm,
∴AF=32+42=5(cm),FC=9﹣3=6(cm),
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t﹣5+6,QA=13﹣4t,
∴5t﹣5+6=13﹣4t,解得t=43,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t=43秒.
七.反证法
19.已知△ABC中,AB=AC,求证:∠B<90°.下面写出运用反证法证明这个命题的四个步骤:
①所以∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾;
②因此假设不成立,所以∠B<90°;
③假设在△ABC中,∠B≥90°;
④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.
这四个步骤正确的顺序应是 ③④①② .(填序号)
试题分析:根据反证法的一般步骤判断即可.
答案详解:解:运用反证法证明这个命题的四个步骤:1、假设在△ABC中,∠B≥90°,
2、由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°,
3、∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾,
4、因此假设不成立.∴∠B<90°,
所以答案是:③④①②.
20.对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )
A.a⊥cB.b⊥cC.a与c相交D.b与c相交
试题分析:反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断.
答案详解:解:c与b的位置关系有c∥b和c与b相交两种,因此用反证法证明“c∥b”时,应先假设c与b相交.
所以选:D.
21.用反证法证明“若|a|<2,则a2<4”是真命题,第一步应先假设 a2≥4 .
试题分析:直接利用反证法的步骤,即可得出答案.
答案详解:解:用反证法证明“若|a|<2,则a2<4.”是真命题时,第一步应先假设:a2≥4.
所以答案是:a2≥4.
22.若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )
A.至少有一个角是钝角或直角
B.没有一个角是锐角
C.没有一个角是钝角或直角
D.每一个角都是钝角或直角
试题分析:反证法的步骤中,第一步是假设结论不成立,反面成立.
答案详解:解:用反证法证明“四边形中至少有一个角是钝角或直角”时第一步应假设:四边形中没有一个角是钝角或直角.
所以选:C.
八.矩形经典---对角线相等
23.如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F.则线段EF的最小值为( )
A.45B.35C.52D.125
试题分析:连接CD,判断出四边形CEDF是矩形,再根据矩形的对角线相等可得EF=CD,然后根据垂线段最短可得CD⊥AB时线段EF的长最小,进而解答即可.
答案详解:解:如图,连接CD,
∵DE⊥BC,DF⊥AC,∠ACB=90°,
∴四边形CEDF是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时线段EF的长最小,
∵AC=3,BC=4,
∴AB=AC2+BC2=5,
∵四边形CEDF是矩形,
∴CD=EF=AC⋅BCAB=125,
所以选:D.
24.如图,在△ABC中,∠BAC=90°,AB=8,AC=6,M为BC上的一动点,ME⊥AB于E,MF⊥AC于F,N为EF的中点,则MN的最小值为 2.4 .
试题分析:过点A作AM⊥BC于点M′,根据勾股定理求出BC的长,再由三角形的面积公式求出AM′的长.根据题意得出四边形AEMF是矩形,故可得出AM=EF,MN=12AM,当MN最小时,AM最短,此时M与M′重合,据此可得出结论.
答案详解:解:过点A作AM⊥BC于点M′,
∵在△ABC中,∠BAC=90°,AB=8,AC=6,
∴BC=82+62=10,
∴AM′=8×610=245.
∵ME⊥AB于E,MF⊥AC于F,
∴四边形AEMF是矩形,
∴AM=EF,MN=12AM,
∴当MN最小时,AM最短,此时点M与M′重合,
∴MN=12AM′=125=2.4.
所以答案是:2.4.
九.角平分与矩形的融合
25.矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积为( )
A.3cm2B.4cm2
C.12cm2D.4cm2或12cm2
试题分析:根据矩形性质得出AB=CD,AD=BC,AD∥BC,推出∠AEB=∠CBE,求出∠AEB=∠ABE,得出AB=AE,分为两种情况:①当AE=1cm时,求出AB和AD;②当AE=3cm时,求出AB和AD,根据矩形的面积公式求出即可.
答案详解:解:
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE,
①当AE=1cm时,AB=1cm=CD,AD=1cm+3cm=4cm=BC,
此时矩形的面积是1cm×4cm=4cm2;
②当AE=3cm时,AB=3cm=CD,AD=4cm=BC,
此时矩形的面积是:3cm×4cm=12cm2;
所以选:D.
26.如图,在△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交△BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在AC运动到什么位置,四边形AECF是矩形,请说明理由.
试题分析:(1)由题意可证OE=OC,OF=OC,即可得OE=OF;
(2)根据三角形内角和定理可求∠ECF=90°,根据勾股定理可求EF的长,根据直角三角形斜边上中线等于斜边的一半,可得OC的长;
(3)当点O在AC的中点时,且OE=OF可证四边形AECF是平行四边形,再根据∠ECF=90°,可证四边形AECF是矩形.
答案详解:证明:(1)∵CF平分∠ACD,且MN∥BD
∴∠ACF=∠FCD=∠CFO
∴OF=OC
同理可证:OC=OE
∴OE=OF
(2)由(1)知:OF=OC=OE
∴∠OCF=∠OFC,∠OCE=∠OEC
∴∠OCF+∠OCE=∠OFC+∠OEC
而∠OCF+∠OCE+∠OFC+∠OEC=180°
∴∠ECF=∠OCF+∠OCE=90°
∴EF=CE2+CF2=122+52=13
∴OC=12EF=132
(3)当点O移动到AC中点时,四边形AECF为矩形
理由如下:
∵当点O移动到AC中点时
∴OA=OC且OE=OF
∴四边形AECF为平行四边形
又∵∠ECF=90°
∴四边形AECF为矩形
十.矩形与度数的融合
27.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC、BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若∠BDE=15°,求∠EOC的度数;
(3)在(2)的条件下,若AB=2,求矩形ABCD的面积.
试题分析:(1)由平行线的性质易证∠BAD=90°,得出∠BAD=∠ABC=∠ADC=90°,即可得出结论;
(2)由矩形和角平分线的性质得出∠CDE=∠CED=45°,则EC=DC,推出∠CDO=60°,证明△OCD是等边三角形,求出∠OCB=30°,得出∠COE=75°,即可得出结果;
(3)根据直角三角形的性质求出AC,根据勾股定理求出BC,根据矩形的面积公式计算即可.
答案详解:(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,DE平分∠ADC,
∴∠CDE=∠CED=45°,
∴EC=DC,
又∵∠BDE=15°,
∴∠CDO=60°,
又∵矩形的对角线互相平分且相等,
∴OD=OC,
∴△OCD是等边三角形,
∴∠DOC=∠OCD=60°,
∴∠OCB=90°﹣∠DCO=30°,
∵CO=CE,
∴∠COE=(180°﹣30°)÷2=75°;
(3)解:在Rt△ABC中,∠ACB=30°,
∴AC=2AB=4,
由勾股定理得:BC=AC2−AB2=23,
∴S矩形ABCD=23×2=43.
28.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
求证:(1)AC=EF;
(2)四边形ADFE是平行四边形;
(3)AC⊥DF.
试题分析:(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又因为△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF;
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形;
(3)先求∠EAC=90°,由▱ADFE得AE∥DF,可以得∠AGD=90°,则AC⊥DF.
答案详解:证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF,AB=AE,
∴AF=BC,
在Rt△AFE和Rt△BCA中,
∵AF=BCAB=AE,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形;
(3)∵∠EAC=∠EAF+∠BAC=60°+30°=90°,
∵四边形ADFE是平行四边形,
∴AE∥FD,
∴∠EAC=∠AGD=90°,
∴AC⊥DF.
十一.矩形中的折叠--等腰、小勾股。
29.如图,在长方形ABCD中,AD∥BC,AB∥CD,E在AD上.AD=m,AE=n(m>n>0).将长方形沿着BE折叠,A落在A′处,A'E交BC于点G,再将∠A′ED对折,点D落在直线A′E上的D′处,C落在C′处,折痕EF,F在BC上,若D、F、D′三点共线,则BF=( )
A.m+12nB.m−n2C.m+n2D.m﹣n
试题分析:连接DD′,证明∠EFD是直角,然后证明△BEF和△EFE全等即可得出结论.
答案详解:解:如图,
连接DD′,
∵D、F、D′三点共线,四边形EFC′D′是由四边形EFCD翻折得到,
∴△EFD≌△EFD′,∠DEF=∠D′EF,
∴∠EFD=90°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠BFE,
∵∠AEB=∠A′EB,
∴∠BEF=90°,
在△BEF和△DFE中,
∠DEF=∠BFE,EF=EF∠BEF=∠EFD,
∴△BEF≌△DFE(ASA),
∴BF=ED,
∵AD=m,AE=n,
∴BF=ED=m﹣n.
所以选:D.
30.如图,将矩形ABCD沿AE折叠,使点D落在边BC的点F处,已知AB=6cm,BC=10cm,则EC的长为 83 cm.
试题分析:设CE=xcm,根据矩形的性质得出DC=AB=6cm,AD=BC=10cm,∠B=∠C=90°,根据折叠得出AF=AD,DE=EF,根据勾股定理求出BF,求出CF,再根据勾股定理求出x即可.
答案详解:解:设CE=xcm,
∵四边形ABCD是矩形,AB=6cm,BC=10cm,
∴DC=AB=6cm,AD=BC=10cm,∠B=∠C=90°,
∵将矩形ABCD沿AE折叠,使点D落在边BC的点F处,
∴AF=AD=10cm,DE=EF=(6﹣x)cm,
∴BF=AF2−AB2=102−62=8(cm),
∴FC=BC﹣BF=2cm,
在Rt△ECF中,由勾股定理得:EF2=CE2+CF2,
即(6﹣x)2=x2+22,
解得:x=83,
即CE=83cm,
所以答案是:83.
31.已知四边形ABCD,其中AD∥BC,AB⊥BC,将DC沿DE折叠,C落于C',DC'交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点A'(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为 45 度.
试题分析:设∠EDC=x,∠GDF=y,根据折叠性质可知,∠EDG=x,∠ADF=∠CDF=2x+y,然后利用∠ADG=90°列出2x+y+y=90°求得x+y的值即可求得答案.
答案详解:解:设∠EDC=x,∠GDF=y,
由折叠性质可知,∠EDG=x,∠ADF=∠CDF=2x+y,
由∠ADG=90°,得2x+y+y=90°,
∴x+y=45°,
故∠EDF=x+y=45°,
所以答案是:45.
十二.矩形与等面积法的妙用
32.如图,在矩形ABCD中,对角线AC、BD相交于点O,且AD=6,CD=8,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )
A.4.8B.6.4C.9.6D.2.4
试题分析:根据勾股定理求出BD,求出OD、OB,求出三角形DAB面积,求出三角形AOB面积,根据三角形面积公式得出12×AO×PM+12×BO×PN=12,求出即可.
答案详解:解:连接PO,
∵在矩形ABCD中,AB=8,BC=6,
∴AD=BC=6,∠DAB=90°,BO=OD,
由勾股定理得:BD=AD2+BA2=64+36=10,
∴BO=DO=5,
∴S△DAB=12×AD×AB=12×8×6=24,
∴S△AOB=12S△DAB=12,
∴12×AO×PM+12×BO×PN=12,
∴PM+PN=4.8.
所以选:A.
33.如图,在矩形ABCD中,点E是对角线AC上一点,有AE=AB=3BC且BC=a,点P是BE上一动点,则点P到边AB,AC的距离之和PM+PN的值( )
A.有最大值aB.有最小值32a
C.是定值12aD.是定值32a
试题分析:连接BP,作EF⊥AB于点F,根据tan∠CAB=BCAB=BC3BC=33,得∠CAB=30°,可得EF=12AE=32a,利用面积法得S△APE+S△APB=S△ABE,将面积公式代入即可.
答案详解:解:如图,连接BP,作EF⊥AB于点F,则∠EFA=90°,
∵AE=AB=3BC=3a,
在矩形ABCD中,∠ABC=90°,
∴tan∠CAB=BCAB=BC3BC=33,
∴∠CAB=30°,
∴EF=12AE=32a,
∵PM⊥AC,PN⊥AB,
∴S△APE+S△APB=S△ABE,
∴12AE•PM+12AB•PN=12AB•EF,
∵AE=AB,
∴PM+PN=EF=32a,
则点P到边AB,AC的距离之和PM+PN的值是定值32a,
所以选:D.
专题09 压轴大题精选01之动点专练-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题09 压轴大题精选01之动点专练-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题09压轴大题精选01之动点专练原卷版docx、专题09压轴大题精选01之动点专练解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
专题06 易错题集锦06之反比例函数专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题06 易错题集锦06之反比例函数专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题06易错题集锦06之反比例函数专题原卷版docx、专题06易错题集锦06之反比例函数专题解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题05易错题精选05之分式方程及应用专题原卷版docx、专题05易错题精选05之分式方程及应用专题解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。












