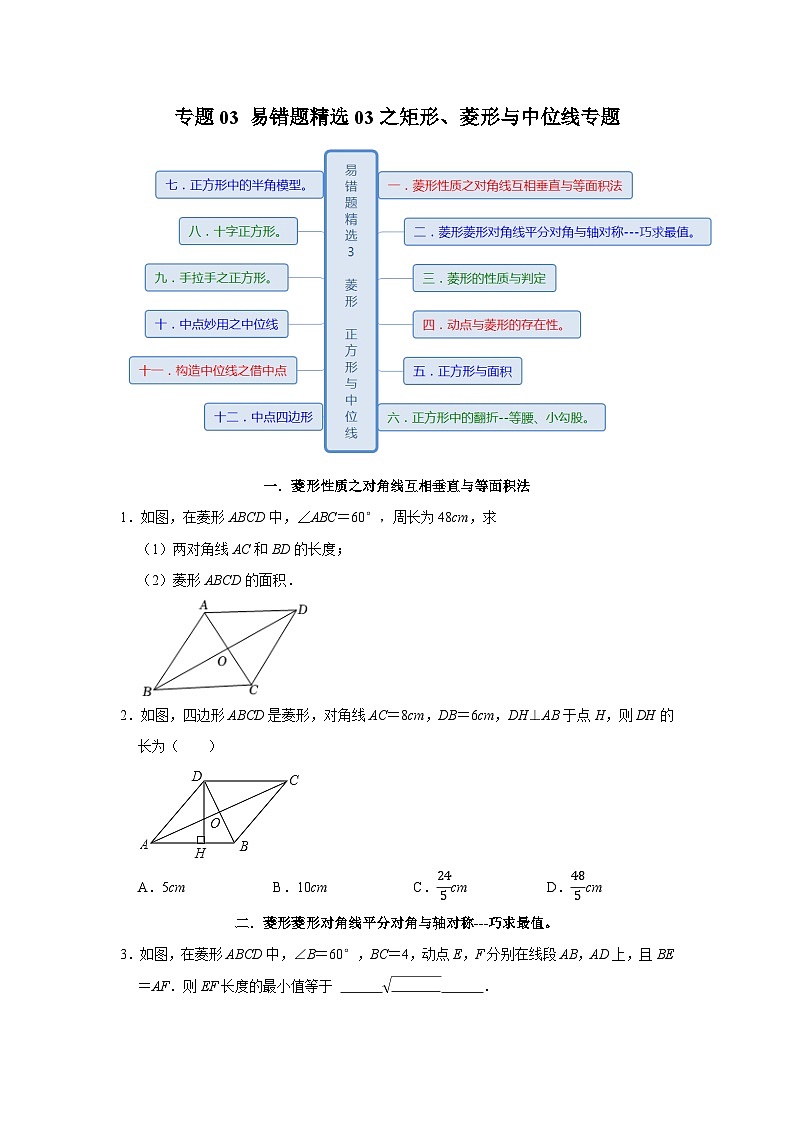
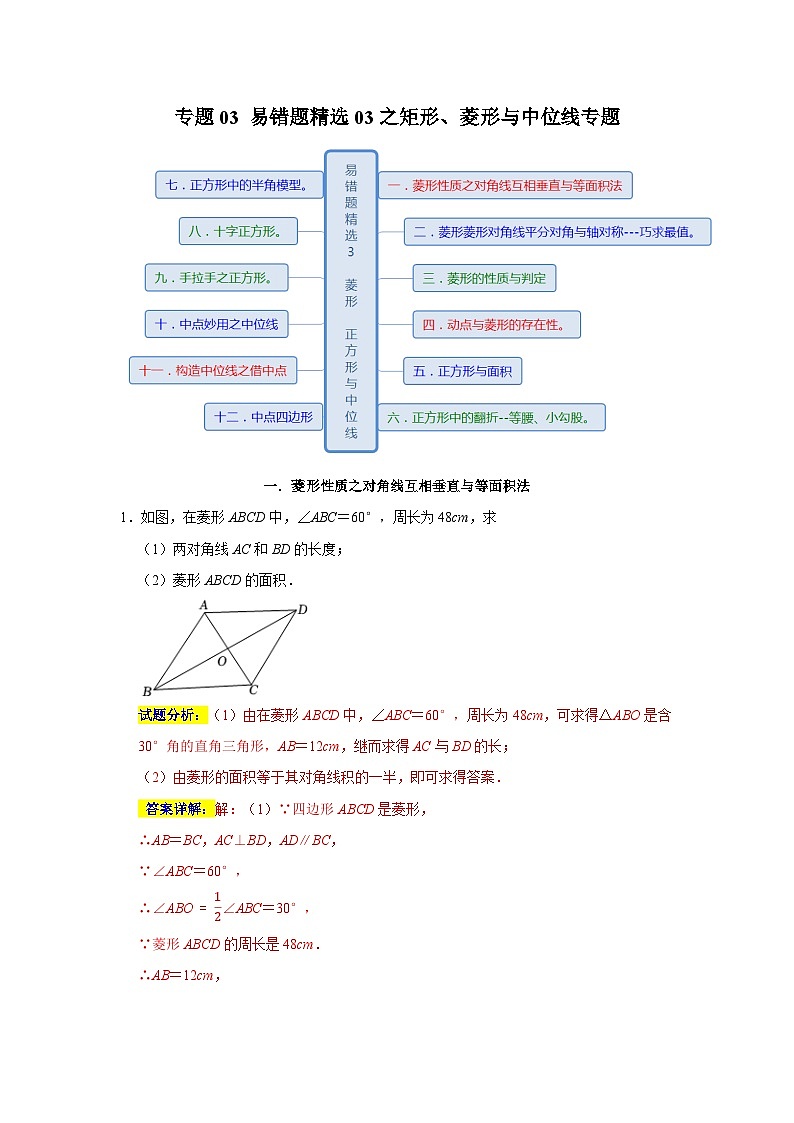
专题03 易错题精选03之矩形、菱形与中位线专题-2023-2024学年八年级数学下学期期末复习培优拔高（苏科版）

这是一份专题03 易错题精选03之矩形、菱形与中位线专题-2023-2024学年八年级数学下学期期末复习培优拔高（苏科版），文件包含专题03易错题精选03之矩形菱形与中位线专题原卷版docx、专题03易错题精选03之矩形菱形与中位线专题解析版docx等2份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。
一．菱形性质之对角线互相垂直与等面积法
1．如图，在菱形ABCD中，∠ABC＝60°，周长为48cm，求
（1）两对角线AC和BD的长度；
（2）菱形ABCD的面积．
试题分析：（1）由在菱形ABCD中，∠ABC＝60°，周长为48cm，可求得△ABO是含30°角的直角三角形，AB＝12cm，继而求得AC与BD的长；
（2）由菱形的面积等于其对角线积的一半，即可求得答案．
答案详解：解：（1）∵四边形ABCD是菱形，
∴AB＝BC，AC⊥BD，AD∥BC，
∵∠ABC＝60°，
∴∠ABO=12∠ABC＝30°，
∵菱形ABCD的周长是48cm．
∴AB＝12cm，
∴OA=12AB＝6cm，
∴OB=AB2−OA2=63，
∴AC＝2OA＝12cm，BD＝2OB＝123cm；
（2）S菱形ABCD=12AC•BD=12×12×123=723（cm2）．
2．如图，四边形ABCD是菱形，对角线AC＝8cm，DB＝6cm，DH⊥AB于点H，则DH的长为（ ）
A．5cmB．10cmC．245cmD．485cm
试题分析：先由勾股定理求出AB，再根据菱形面积的计算方法即可求出结果．
答案详解：解：∵四边形ABCD是菱形，
∴OA=12AC＝4，OB=12BD＝3，AC⊥BD，
∴AB=OA2+OB2=42+32=5，
∵菱形ABCD的面积＝AB•DH=12AC•BD=12×8×6＝24，
∴DH=245；
所以选：C．
二．菱形菱形对角线平分对角与轴对称---巧求最值。
3．如图，在菱形ABCD中，∠B＝60°，BC＝4，动点E，F分别在线段AB，AD上，且BE＝AF．则EF长度的最小值等于 23 ．
试题分析：连接AC，先证△BCE≌△ACF（SAS），得CE＝CF，∠BCE＝∠ACF，再证△CEF是等边三角形，得EF＝CE，当CE最小时，EF也最小，然后求出CE的最小值，即可解决问题．
答案详解：解：如图，连接AC，
∵四边形ABCD是菱形，
∴AB＝BC＝4，AD∥BC，
∵∠B＝60°，
∴△ABC是等边三角形，
∴AC＝BC，∠ACB＝60°，
∵AD∥BC，
∴∠CAF＝∠ACB＝60°，
∴∠B＝∠CAF，
在△BCE和△ACF中，
BE=AF∠B=∠CAFBC=AC，
∴△BCE≌△ACF（SAS），
∴CE＝CF，∠BCE＝∠ACF，
∴∠ACF+∠ACE＝∠BCE+∠ACE＝∠ACB＝60°，
∴△CEF是等边三角形，
∴EF＝CE，
∴当CE最小时，EF也最小，
当CE⊥AB时，CE最小，
此时∠BCE＝90°﹣∠B＝30°，
∴BE=12BC＝2，
∴CE=BC2−BE2=42−22=23，
∴EF的最小值为23，
所以答案是：23．
4．如图，菱形ABCD的对角线AC、BD相交于O，点H是线段BC的动点，连接OH．若OB＝4，S菱形ABCD＝24，则OH的最小值是 2.4 ．
试题分析：根据菱形面积等于对角线乘积的一半求出AC，再由动点H运动特点知OH最小即OH⊥BC时，由直角三角形面积公式即可得出结果．
答案详解：解：∵四边形ABCD是菱形，
∴AC⊥BD，BO＝DO＝4，OA＝CO，
∴BD＝8，
∵S菱形ABCD=12AC•BD＝24，
∴AC=2412BD=2412×8=6，
∴OA＝CO＝3，
由勾股定理得：BC=CO2+BO2=32+42=5，
∵当OH最小时，OH⊥BC，
此时S△OBC=12BO•CO=12BC•OH，
∴OH=BO⋅COBC=4×35=2.4，
即OH最小值为2.4，
所以答案是：2.4．
5．已知四边形ABCD为菱形，∠BAD＝60°，AB＝6cm，P为AC上任一点，则PD+12PA的最小值是 33 cm．
试题分析：根据菱形的性质，可得AC是BD的垂直平分线，可得AC上的点到D、B点的距离相等，连接BE交AC于P，过P点作PH⊥AB，将12PA转化为PH，当PDH三点在同一直线时，PD+12PA＝PH取最小值．可得答案．
答案详解：解：过P点作PH⊥AB，
∵四边形ABCD为菱形，∠BAD＝60°，
∴∠DAC＝30°，
∴PH=12PA，
又∵菱形的对角线互相垂直平分，可得B、D关于AC对称，连接PB．则PD＝PB，
∴PD+12PA＝PD+PH
即当P，D，H三点在同一直线时，PD+12PA＝PH取最小值．
∵∠BAD＝60°，AD＝AB＝6，
∴△ABD是等边三角形，
过D点作DH'⊥AB，
∵AH'＝BH'＝3，
在△AD'H中，DH'=AD2−H'A2=62−32=33，即 最小值为33．
所以答案是：33．
6．如图，将两张长为9，宽为3的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的面积有最小值9，那么菱形面积的最大值是 15 ．
试题分析：当两张纸条如图所示放置时，菱形面积最大，然后根据勾股定理求出菱形的边长，然后根据菱形的面积公式计算即可．
答案详解：解：如图，
此时菱形ABCD的面积最大．
设AB＝x，EB＝9﹣x，AE＝3，
则由勾股定理得到：32+（9﹣x）2＝x2，
解得 x＝5，
S最大＝5×3＝15；
所以答案是：15．
三．菱形的性质与判定
7．如图，在Rt△ABC中，∠BAC＝90°，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥BC，DE与AC，AE分别交于点O，E，连接EC．求证：四边形ADCE是菱形．
试题分析：根据平行四边形的判定和性质定理得到AE＝BD，根据直角三角形的性质得到BD＝CD，根据菱形的判定定理即可得到结论．
答案详解：证明：∵AE∥BC，DE∥AB，
∴四边形ABDE为平行四边形，
∴AE＝BD，
∵AD是边BC上的中线，
∴BD＝CD，
∴AE＝CD，
∴四边形ADCE是平行四边形，
又∵∠BAC＝90°，AD是边BC上的中线，
∴AD=12BC＝CD，
∴平行四边形ADCE是菱形．
8．如图，在四边形ABCD中，AD∥BC，对角线BD的垂直平分线与边AD、BC分别相交于点M、N．求证：四边形BNDM是菱形．
试题分析：证明△MOD≌△NOB（AAS），得出OM＝ON，再由OB＝OD，证出四边形BNDM是平行四边形，进而得出结论．
答案详解：证明：∵AD∥BC，
∴∠DMO＝∠BNO，
∵MN是对角线BD的垂直平分线，
∴OB＝OD，MN⊥BD，
在△MOD和△NOB中，
∠DMO=∠BNO∠MOD=∠MOBOD=OB，
∴△MOD≌△NOB（AAS），
∴OM＝ON，
∵OB＝OD，
∴四边形BNDM是平行四边形，
∵MN⊥BD，
∴平行四边形BNDM是菱形．
9．如图，在平行四边形ABCD中，对角线AC与BD相交于点O．过点O的直线EF与BA，DC的延长线分别相交于点E，F．
（1）求证：AE＝CF；
（2）如果BD⊥EF，求证：四边形BEDF是菱形．
试题分析：（1）证明△AOE≌△COF（AAS），即可得出结论；
（2）由平行四边形的性质得到OB＝OD，再由全等三角形的性质得到OE＝OF，则四边形BFDE是平行四边形，然后由菱形的判定即可得出结论．
答案详解：证明：（1）∵四边形ABCD是平行四边形，
∴OA＝OC，AB∥CD，
∴∠AEO＝∠CFO，
在△AOE和△COF中，
∠AEO=∠CFO∠AOE=∠COFOA=OC，
∴△AOE≌△COF（AAS），
∴AE＝CF；
（2）∵四边形ABCD是平行四边形，
∴OB＝OD，
由（1）得：△AOE≌△COF，
∴OE＝OF，
∴四边形BEDF是平行四边形，
∵BD⊥EF，
∴平行四边形BEDF是菱形．
四．动点与菱形的存在性。
10．如图，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以6cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以3cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t秒（0＜t≤10）．过点D作DF⊥BC于点F，连接DE，EF．四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由．
试题分析：证四边形AEFD是平行四边形，当AD＝AE时，平行四边形AEFD是菱形，可得关于t的方程，求解即可．
答案详解：解：四边形AEFD能成为菱形．理由如下：
∵Rt△ABC中，∠B＝90°，∠A＝60°，
∴∠C＝90°﹣∠A＝30°．
在Rt△CDF中，∠C＝30°，CD＝6tcm，
∴DF=12CD＝3t（cm），
∵点E从点A出发沿AB方向以3cm/秒的速度向点B匀速运动，
∴AE＝3tcm，
∴AE＝DF；
∵∠B＝90°，DF⊥BC，
∴DF∥AB，
又∵AE＝DF，
∴四边形AEFD是平行四边形，
当AD＝AE时，平行四边形AEFD是菱形，
∵AC＝60cm，
∴AD＝（60﹣6t）cm，
∵AE＝3tcm，
∴60﹣6t＝3t，
解得：t=203，
即四边形AEFD能够成为菱形，相应的t值为203．
11．如图，平行四边形ABCD的对角线AC，BD相交于点O，BD＝12cm，AC＝6cm，点E在线段BO上从点B出发以1cm/s的速度向点O运动，点F在线段OD上从点O出发以2cm/s的速度向点D运动．
（1）若点E，F同时运动，设运动时间为ts，当t为何值时，四边形AECF是平行四边形？
（2）在（1）的条件下，当AB为何值时，平行四边形AECF是菱形？
试题分析：（1）若是平行四边形，所以BD＝12cm，则B0＝DO＝6cm，故有6﹣1t＝2t，即可求得t值；
（2）由菱形的性质得AC⊥EF，再由勾股定理求出AB的长即可．
答案详解：解：（1）若四边形AECF为平行四边形，
则OA＝OC，OE＝OF，
∵四边形ABCD为平行四边形，BD＝12cm，AC＝6cm，
∴BO＝OD＝6cm，OA＝OC＝3cm，
∴OE＝（6﹣t）cm，OF＝2tcm，
∴6﹣t＝2t，
∴t＝2，
∴当t为2时，四边形AECF是平行四边形；
（2）若四边形AECF是菱形，
则AC⊥EF，
∴AO2+BO2＝AB2，
∴AB=32+62=35（cm），
∴当AB为35cm时，▱AECF是菱形．
五．正方形与面积
12．将五个边长都为4cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和为 16 cm2．
试题分析：如图，连接AM、AF．由△AME≌△AFG（ASA），推出S△AME＝S△AFG，推出S四边形AEMG＝S△AMF=14S正方形，推出S阴＝4×14S正方形＝16即可解决问题．
答案详解：解：如图，连接AM、AF．
∵∠EAG＝∠MAF＝90°，
∴∠MAE＝∠FAG，
在△AME和△AFG中，
∠AME=∠AFG=45°AM=AF∠MAE=∠FAG，
∴△AME≌△AFG（ASA），
∴S△AME＝S△AFG，
∴S四边形AEMG＝S△AMF=14S正方形，
∴S阴＝4×14S正方形＝16（cm2），
所以答案是：16．
六．正方形中的翻折--等腰、小勾股。
13．如图，在正方形ABCD中，点E，F分别在边AB，CD上，∠EFC＝120°，若将四边形EBCF沿EF折叠，点B恰好落在AD边上，则∠AEB′为（ ）
A．70°B．65°C．30°D．60°
试题分析：依据正方形的性质以及折叠的性质，即可得到∠AEB'＝60°．
答案详解：解：∵四边形ABCD是正方形，
∴AB∥CD，
∴∠BEF+∠EFC＝180°，
∵∠EFC＝120°，
∴∠BEF＝180°﹣∠EFC＝60°，
∵将四边形EBCF沿EF折叠，点B恰好落在AD边上，
∴∠BEF＝∠FEB'＝60°，
∴∠AEB'＝180°﹣∠BEF﹣∠FEB'＝60°，
所以选：D．
14．如图，一张矩形纸片，按照下面步骤进行折叠：
第一步，在矩形纸片的一端，利用图①的方法折出一个正方形，然后把纸片展平．
第二步，如图②，把这个正方形折成两个相等的矩形，再把纸片展平．
第三步，折出内侧矩形的对角线AB，并把AB折到图③中所示的AD处．
第四步，展平纸片，按照所得的点D折出DE，得出矩形BCDE（图④）．则矩形BCDE的宽与长的比为 5−12 ．
试题分析：设BC＝NC＝MN＝2a，由折叠的性质可求AC＝a，由勾股定理可求AB的长，由折叠的性质可求CD的长，即可求解．
答案详解：解：设BC＝NC＝MN＝2a，
∵把这个正方形折成两个相等的矩形，
∴NA＝AC＝a，
∴AB=AC2+BC2=5a，
∵并把AB折到图③中所示的AD处．
∴AD＝AB=5a，
∴CD＝（5−1）a，
∴矩形BCDE的宽与长的比=5−12，
所以答案是：5−12．
15．对下列现象中蕴含的数学原理阐述正确的是 ①③④ （填序号）
①如图（1），剪两张对边平行的纸条，随意交叉叠放在一起，重合的部分构成一个平行四边形．其依据是两组对边分别平行的四边形是平行四边形．
②如图（2），工人师傅在做矩形门窗时，不仅测量出两组对边的长度是否相等，还要测量出两条对角线的长度相等，以确保图形是矩形．其依据是对角线相等的四边形是矩形．
③如图（3），将两张等宽的纸条放在一起，重合部分构成的四边形ABCD一定是菱形．其依据是一组邻边相等的平行四边形是菱形．
④如图（4），把一张长方形纸片按如图方式折一下，就可以裁出正方形．其依据是一组邻边相等的矩形是正方形．
试题分析：①平行四边形的判定定理：两组对边分别平行的四边形是平行四边形；
②矩形的判定定理：对角线相等的平行四边形是矩形；
③首先可判断重叠部分为平行四边形，且两条纸条宽度相同；再由平行四边形的等积转换可得邻边相等，则重叠部分为菱形；
④根据折叠定理得：所得的四边形有三个直角，且一组邻边相等，所以可以裁出正方形纸片．
答案详解：解：①由题意得：AB∥CD，AD∥BC，
∵两组对边分别平行，
∴四边形ABCD是平行四边形，故正确；
②∵两组对边的长度相等，
∴四边形是平行四边形，
∵对角线相等，
∴此平行四边形是矩形，故错误；
③∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形，
∴AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形（对边相互平行的四边形是平行四边形）；
过点D分别作AB，BC边上的高为DE，DF．如图所示：
则DE＝DF（两纸条相同，纸条宽度相同）；
∵平行四边形ABCD的面积＝AB×DE＝BC×DF，
∴AB＝BC．
∴平行四边形ABCD为菱形（一组邻边相等的平行四边形是菱形），故正确；
④根据折叠原理，对折后可得：
所得的四边形有三个直角，且一组邻边相等，
所以可以裁出正方形纸片，故正确．
所以答案是①③④．
七．正方形中的半角模型。
16．已知：正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．
（1）如图1，当∠MAN绕点A旋转到BM＝DN时，有BM+DN＝MN．当∠MAN绕点A旋转到BM≠DN时，如图2，请问图1中的结论还是否成立？如果成立，请给予证明，如果不成立，请说明理由；
（2）当∠MAN绕点A旋转到如图3的位置时，线段BM，DN和MN之间有怎样的等量关系？请写出你的猜想，并证明．
试题分析：（1）在MB的延长线上截取BE＝DN，连接AE，根据正方形性质得出AD＝AB，∠D＝∠DAB＝∠ABC＝∠ABE＝90°，证△ABE≌△ADN推出AE＝AN；∠EAB＝∠NAD，求出∠EAM＝∠MAN，根据SAS证△AEM≌△ANM，推出ME＝MN即可；
（2）在DN上截取DE＝MB，连接AE，证△ABM≌△ADE，推出AM＝AE；∠MAB＝∠EAD，求出∠EAN＝∠MAN，根据SAS证△AMN≌△AEN，推出MN＝EN即可．
答案详解：解：（1）图1中的结论仍然成立，即BM+DN＝MN，理由为：
如图2，在MB的延长线上截取BE＝DN，连接AE，
∵四边形ABCD是正方形，
∴AD＝AB，∠D＝∠DAB＝∠ABC＝∠ABE＝90°，
∵在△ABE和△ADN中
AD=AB∠D=∠ABEDN=BE，
∴△ABE≌△ADN（SAS）．
∴AE＝AN；∠EAB＝∠NAD，
∵∠DAB＝90°，∠MAN＝45°，
∴∠DAN+∠BAM＝45°，
∴∠EAM＝∠BAM+∠EAB＝45°＝∠MAN，
∵在△AEM和△ANM中
AE=AN∠EAM=∠NAMAM=AM，
∴△AEM≌△ANM（SAS），
∴ME＝MN，
∴MN＝ME＝BE+BM＝DN+BM，
即DN+BM＝MN；
（2）猜想：线段BM，DN和MN之间的等量关系为：DN﹣BM＝MN．
证明：如图3，在DN上截取DE＝MB，连接AE，
∵由（1）知：AD＝AB，∠D＝∠ABM＝90°，BM＝DE，
∴△ABM≌△ADE（SAS）．
∴AM＝AE；∠MAB＝∠EAD，
∵∠MAN＝45°＝∠MAB+∠BAN，
∴∠DAE+∠BAN＝45°，
∴∠EAN＝90°﹣45°＝45°＝∠MAN，
∵在△AMN和△AEN中
AM=AE∠MAN=∠EANAN=AN，
∴△AMN≌△AEN（SAS），
∴MN＝EN，
∵DN﹣DE＝EN，
∴DN﹣BM＝MN．
17．如图1，在正方形ABCD中，E、F分别是BC，CD上的点，且∠EAF＝45度．则有结论EF＝BE+FD成立；
（1）如图2，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是BC，CD上的点，且∠EAF是∠BAD的一半，那么结论EF＝BE+FD是否仍然成立？若成立，请证明；不成立，请说明理由．
（2）若将（1）中的条件改为：如图3，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，延长BC到点E，延长CD到点F，使得∠EAF仍然是∠BAD的一半，则结论EF＝BE+FD是否仍然成立？若成立，请证明；不成立，请写出它们的数量关系并证明．
试题分析：（1）结论仍然成立．延长CB到G，使BG＝FD，根据已知条件容易证明△ABG≌△ADF，由此可以推出∠BAG＝∠DAF，AG＝AF，而∠EAF=12∠BAD，所以得到∠DAF+∠BAE＝∠EAF，进一步得到∠EAF＝∠GAE，现在可以证明△AEF≌△AEG，然后根据全等三角形的性质就可以证明结论成立；
（2）结论不成立，应为EF＝BE﹣DF，如图在CB上截取BG＝FD，由于∠B+∠ADC＝180°，∠ADF+∠ADC＝180°，可以得到∠B＝∠ADF，再利用已知条件可以证明△ABG≌△ADF，由此可以推出∠BAG＝∠DAF，AG＝AF，而∠EAF=12∠BAD，所以得到∠EAF＝∠GAE，现在可以证明△AEF≌△AEG，再根据全等三角形的性质就可以证明EF＝EG＝EB﹣BG＝EB﹣DF．
答案详解：解：（1）延长CB到G，使BG＝FD，连接AG，
∵∠ABG＝∠D＝90°，AB＝AD，
∴△ABG≌△ADF，
∴∠BAG＝∠DAF，AG＝AF，
∵∠EAF=12∠BAD，
∴∠DAF+∠BAE＝∠EAF，
∴∠EAF＝∠GAE，
∴△AEF≌△AEG，
∴EF＝EG＝EB+BG＝EB+DF．
（2）结论不成立，应为EF＝BE﹣DF，
证明：在BE上截取BG，使BG＝DF，连接AG．
∵∠B+∠ADC＝180°，∠ADF+∠ADC＝180°，
∴∠B＝∠ADF．
∵AB＝AD，
∴△ABG≌△ADF．
∴∠BAG＝∠DAF，AG＝AF．
∴∠BAG+∠EAD＝∠DAF+∠EAD
＝∠EAF=12∠BAD．
∴∠GAE＝∠EAF．
∵AE＝AE，
∴△AEG≌△AEF．
∴EG＝EF
∵EG＝BE﹣BG
∴EF＝BE﹣FD．
八．十字正方形。
18．如图，E、F分别是正方形ABCD的边CD，AD上的点，且CE＝DF，AE，BF相交于点O，下列结论①AE＝BF；②AE⊥BF；③AO＝OE；④S△AOB＝S四边形DEOF中，正确结论的个数为（ ）
A．4个B．3个C．2个D．1个
试题分析：根据正方形的性质可得∠BAF＝∠D＝90°，AB＝AD＝CD，然后求出AF＝DE，再利用“边角边”证明△ABF和△DAE全等，根据全等三角形对应边相等可得AE＝BF，从而判定出①正确；再根据全等三角形对应角相等可得∠ABF＝∠DAE，然后证明∠ABF+∠BAO＝90°，再得到∠AOB＝90°，从而得出AE⊥BF，判断②正确；假设AO＝OE，根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AB＝BE，再根据直角三角形斜边大于直角边可得BE＞BC，即BE＞AB，从而判断③错误；根据全等三角形的面积相等可得S△ABF＝S△ADE，然后都减去△AOF的面积，即可得解，从而判断④正确．
答案详解：解：在正方形ABCD中，∠BAF＝∠D＝90°，AB＝AD＝CD，
∵CE＝DF，
∴AD﹣DF＝CD﹣CE，
即AF＝DE，
在△ABF和△DAE中，AB=AD∠BAF=∠D=90°AF=DE，
∴△ABF≌△DAE（SAS），
∴AE＝BF，故①正确；
∠ABF＝∠DAE，
∵∠DAE+∠BAO＝90°，
∴∠ABF+∠BAO＝90°，
在△ABO中，∠AOB＝180°﹣（∠ABF+∠BAO）＝180°﹣90°＝90°，
∴AE⊥BF，故②正确；
假设AO＝OE，
∵AE⊥BF（已证），
∴AB＝BE（线段垂直平分线上的点到线段两端点的距离相等），
∵在Rt△BCE中，BE＞BC，
∴AB＞BC，这与正方形的边长AB＝BC相矛盾，
所以，假设不成立，AO≠OE，故③错误；∵△ABF≌△DAE，
∴S△ABF＝S△DAE，
∴S△ABF﹣S△AOF＝S△DAE﹣S△AOF，
即S△AOB＝S四边形DEOF，故④正确；
综上所述，错误的有③．
所以选：B．
19．在正方形ABCD中：
（1）如图①，点E、F分别在BC、CD上，且AE⊥BF，垂足为M．求证：AE＝BF．
（2）如图②，如果点E、F、G、H分别在BC、CD、DA、AB上，且GE⊥HF，垂足M．那么GE、HF相等吗？证明你的结论．
（3）如图③，在等边三角形ABC中，点E、F分别在BC、CA上，且BE＝CF，你能猜想∠AMF的度数吗？证明你的结论．
试题分析：有三角形的直接证明三角形全等，没三角形的构造直角三角形，利用正方形的性质证明三角形全等；对于第4问也是证明三角形全等，再用角等量代换求解．
答案详解：（1）证明：∵AE⊥BF，
∴∠BAE+∠ABM＝90°，∠CBF+∠ABM＝90°，
∴∠BAE＝∠CBF，
在△BAE和△CBF中
∠BAE=∠CBF∠ABC=∠BCFAB=BC，
△BAE≌△CBF（AAS），
∴AE＝BF；
（2）结论：HF＝GE
分别过G、H作GT⊥BC、HN⊥CD，
∴GT⊥HN，
∴∠FHN+∠HPO＝90°，∠EGT+∠GPM＝90°，∠GPM＝∠HPO，
∴∠FHN＝∠EGT，
∵HN＝GT，∠GTE＝∠NHF＝90°，
在△GTE与△HNF中，
∠FHN=∠EGTHN=GT∠GTE=∠NHF，
∴△GTE≌△HNF，
∴GE＝HF；
（3）结论：∠AMF＝60°．
在△ABE和△BCF中
AB=BC∠ABC=∠BE=CFBCF，
∴△ABE≌△BCF（SAS），
∴∠BAE＝∠CBF，
∴∠ABE＝∠BME＝60°，
∴∠AMF＝∠BME＝60°．
九．手拉手之正方形。
20．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系．
（1）猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系；
（2）将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度a，得到如图2、如图3情形．请你通过观察、测量等方法判断（1）中得到的结论是否仍然成立，并选取图2证明你的判断．
试题分析：（1）根据正方形的性质，显然三角形BCG顺时针旋转90°即可得到三角形DCE，从而判断两条直线之间的关系；
（2）结合正方形的性质，根据SAS仍然能够判定△BCG≌△DCE，从而证明结论．
答案详解：解：（1）BG＝DE，BG⊥DE；
∵四边形ABCD和四边形CEFG是正方形，
∴BC＝DC，CG＝CE，∠BCD＝∠ECG＝90°，
∴∠BCG＝∠DCE，
在△BCG和△DCE中，
BC＝DC∠BCG＝∠DCECG＝CE，
∴△BCG≌△DCE（SAS），
∴BG＝DE；
延长BG交DE于点H，
∵△BCG≌△DCE，
∴∠CBG＝∠CDE，
又∠CBG+∠BGC＝90°，
∴∠CDE+∠DGH＝90°，
∴∠DHG＝90°，
∴BH⊥DE，即BG⊥DE；
（2）BG＝DE，BG⊥DE仍然成立，
在图（2）中证明如下
∵四边形ABCD、四边形CEFG都是正方形
∴BC＝CD，CG＝CE，∠BCD＝∠ECG＝90°
∴∠BCG＝∠DCE，
∴△BCG≌△DCE（SAS）
∴BG＝DE，∠CBG＝∠CDE，
又∵∠BHC＝∠DHO，∠CBG+∠BHC＝90°
∴∠CDE+∠DHO＝90°
∴∠DOH＝90°
∴BG⊥DE．
21．如图，正方形ABCD和正方形CEFG的边长分别为a和b，BE和DG相交于点H，连接HC，给出下列结论：①BE＝DG；②BE⊥DG；③DE2+BG2＝2a2+2b2；④HC平分∠BHG，其中正确结论是（ ）
A．只有①②③B．只有①②④C．只有②③④D．①②③④
试题分析：根据正方形性质可证明△BCE≌△DCG（SAS），可得BE＝DG，∠CBE＝∠CDG，再利用三角形内角和定理即可证明∠DHT＝90°，即BE⊥DG，依据勾股定理可得：DE2+BG2＝2a2+2b2，由∠BHD＝∠BCD＝90°可知B、C、H、D四点共圆，进而可证∠BHC＝∠BDC＝45°，可得HC平分∠BHG．
答案详解：解：如图，∵正方形ABCD和正方形CEFG
∴BC＝CD＝a，CE＝CG＝b，∠BCD＝∠ECG＝90°
∴∠BCD+∠DCE＝∠ECG+∠DCE，即∠BCE＝∠DCG
∴△BCE≌△DCG（SAS）
∴BE＝DG，∠CBE＝∠CDG
故①正确；
设BE与CD交于T，
∵∠CBE+∠BTC＝90°，∠BTC＝∠DTE
∴∠CDG+∠DTE＝90°，
∴∠DHT＝90°
∴BE⊥DG
故②正确；
连接BD，EG，在Rt△DEH中，DE2＝DH2+EH2，在Rt△BGH中，BG2＝BH2+GH2
在Rt△BDH中，BH2+DH2＝BD2，在Rt△EHG中，EH2+GH2＝EG2，
∴DE2+BG2＝DH2+EH2+BH2+GH2＝BD2+EG2，
在Rt△BCD中，BD2＝BC2+CD2＝2a2，在Rt△CEG中，EG2＝CE2+CG2＝2b2，
∴DE2+BG2＝2a2+2b2，
故③正确；
∵∠BHD＝∠BCD＝90°
∴B、C、H、D四点共圆，
∴∠BHC＝∠BDC＝45°，
∴∠GHC＝∠BHG﹣∠BHC＝45°
∴∠BHC＝∠GHC
∴HC平分∠BHG，
（过点C作CQ⊥BT，CR⊥DG，利用全等三角形的性质证明也可以）．
故④正确；
所以选：D．
十．中点妙用之中位线
22．如图，在△ABC中，D，E分别是BC，AC的中点，F是AB边上的一个动点，连结DE，EF，FD．若△ABC的面积为20，则△DEF的面积是（ ）
A．3B．4C．5D．6
试题分析：连接BE，根据三角形的面积公式求出△DEB的面积，根据三角形中位线定理得到DE∥AB，得到△DEF的面积＝△DEB的面积，得到答案．
答案详解：解：连接BE，
∵点E是AC的中点，△ABC的面积的为20，
∴△CEB的面积=12×△ABC的面积＝10，
∵点D是AB的中点，
∴△DEB的面积=12×△CEB的面积＝5，
∵D，E分别是BC，AC的中点，
∴DE∥AB，
∴△DEF的面积＝△DEB的面积＝5，
所以选：C．
23．如图在四边形ABCD中，E，F分别是AB，CD的中点，G，H分别是对角线BD，AC的中点，若HF＝5，则EG的长为（ ）
A．10B．2.5C．5D．3.5
试题分析：根据三角形中位线定理解答即可．
答案详解：解：∵F、H分别是CD，CA边的中点，
∴HF是△ACD的中位线，
∴HF=12AD．
∵E、G分别是AB，BD边的中点，
∴EG是△ABC的中位线，
∴EG=12AD．
∴EG＝HF＝5．
所以选：C．
24．如图，△ABC的周长为64，E、F、G分别为AB、AC、BC的中点，A'、B'、C'分别为EF、EG、GF的中点，如果△ABC、△EFG、△A'B'C'分别为第1个、第2个、第3个三角形，按照上述方法继续作三角形，那么第n个三角形的周长是（ ）
A．64×(12)nB．64×(12)n−1
C．32×(12)nD．32×(12)n−1
试题分析：根据三角形中位线定理得到EF=12BC，EG=12AC，FG=12AB，进而求出△EFG的周长，根据题意总结规律，根据规律解答即可．
答案详解：解：∵E、F、G分别为AB、AC、BC的中点，
∴EF=12BC，EG=12AC，FG=12AB，
∴△EFG的周长为：64×12，
同理可得：△A'B'C'的周长为：64×（12）2，
……
则第n个三角形的周长为：64×（12）n﹣1，
所以选：B．
十一．构造中位线之借中点
25．如图，DE垂直平分△ABC的边AB，交CB的延长线于点D，交AB于点E，F是AC的中点，连结AD、EF．若AD＝5，CD＝9，则EF的长为（ ）
A．3B．2.5C．2D．1.5
试题分析：根据线段垂直平分线的性质得到DB＝AD＝5，AE＝EB，进而求出BC，根据三角形中位线定理计算即可．
答案详解：解：∵DE垂直平分AB，AD＝5，
∴DB＝AD＝5，AE＝EB，
∵CD＝9，
∴BC＝CD﹣BD＝9﹣5＝4，
∵AE＝EB，AF＝FC，
∴EF=12BC＝2，
所以选：C．
26．如图，已知四边形ABCD的对角线AC与BD相交于点O，且AC＝BD，M、N分别是AB、CD的中点，MN分别交BD、AC于点E、F．你能说出OE与OF的大小关系并加以证明吗？
试题分析：此题要构造三角形的中位线，根据三角形的中位线定理进行证明．
答案详解：解：相等．理由如下：
取AD的中点G，连接MG，NG，
∵G、N分别为AD、CD的中点，
∴GN是△ACD的中位线，
∴GN=12AC，
同理可得，GM=12BD，
∵AC＝BD，
∴GN＝GM=12AC=12BD．
∴∠GMN＝∠GNM，
又∵MG∥OE，NG∥OF，
∴∠OEF＝∠GMN＝∠GNM＝∠OFE，
∴OE＝OF．
27．如图，在△ABC中，BC＝10，D，E分别是AB，AC的中点，F是DE上一点，DF＝1，连接AF，CF，若∠AFC＝90°，则AC的长度为（ ）
A．8B．10C．12D．14
试题分析：根据三角形中位线定理求出DE，进而求出EF，再根据直角三角形斜边上的中线的性质计算即可．
答案详解：解：∵D，E分别是AB，AC的中点，
∴DE是△ABC的中位线，
∴DE=12BC＝5，
∵DF＝1，
∴EF＝5﹣1＝4，
在Rt△AFC中，E是AC的中点，
∴AC＝2EF＝2×4＝8，
所以选：A．
十二．中点四边形
28．如图，点D是△ABC内一点，BD⊥CD，AD＝11，BD＝8，CD＝6，点E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（ ）
A．14B．18C．21D．24
试题分析：利用勾股定理列式求出BC的长，再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH＝FG=12AD，EF＝GH=12BC，然后代入数据进行计算即可得解．
答案详解：解：∵BD⊥CD，BD＝8，CD＝6，
∴BC=BD2+CD2=82+62=10，
∵E、F、G、H分别是AB、AC、CD、BD的中点，
∴EH＝FG=12AD，EF＝GH=12BC，
∴四边形EFGH的周长＝EH+GH+FG+EF＝AD+BC，
又∵AD＝11，
∴四边形EFGH的周长＝11+10＝21．
所以选：C．
29．如图，在四边形ABCD中，AC＝a，BD＝b，且AC⊥BD，垂足为O，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2…，如此进行下去，得到四边形AnBn∁nDn．下列结论正确的有（ ）
①A1D1是△ABD的中位线；
②A2D2是△ABO的中位线；
③四边形A4B4C4D4是菱形；
④四边形AnBn∁nDn的面积是ab2n+1．
A．①②B．①③C．①③④D．①②③④
试题分析：首先根据题意，找出变化后的四边形的边长与四边形ABCD中各边长的长度关系规律，然后对以下选项作出分析与判断：
①根据中位线的定义进行分析即可；
②根据中位线的定义进行分析即可；
③根据菱形的判定定理推断；
④根据四边形AnBn∁nDn的面积与四边形ABCD的面积间的数量关系来求其面积．
答案详解：解：∵A1是AB的中点，D1是AD的中点，
∴A1D1是△ABD的中位线，故①正确；
∵A2和D2不在△ABO的边上（即不是△ABO的边的中点），
∴A2D2不是△ABO的中位线，故②错误；
∵A1、D1、B1、C1分别是边AB、AD、BC、CD的中点，
∴D1C1∥AC，A1D1=12BD，B1C1=12BD，A1D1∥BD，B1C1∥BD，
∴A1D1∥B1C1，A1D1＝B1C1，
∴四边形A1B1C1D1是平行四边形，
同理四边形A2B2C2D2是平行四边形，
∵D1C1∥AC，A1D1∥BD，AC⊥BD，
∴B1C1∥D1C1，
即∠D1C1B1＝90°，
∴四边形A1B1C1D1是矩形，
∴A1C1＝B1D1，
∵A2、B2、C2、D2分别是A1B1、B1C1、C1D1、A1D1的中点，
∴A2D2=12B1D1，D2C2=12A1C1，
∴A2D2＝D2C2，
∴四边形A2B2C2D2是菱形，
同理四边形A3B3C3D3是矩形，四边形A4B4C4D4是菱形，故③正确；
④∵四边形ABCD中，AC＝a，BD＝b，且AC⊥BD，
∴S四边形ABCD=12ab．
由三角形的中位线的性质可以推知，每得到一次四边形，它的面积变为原来的一半，
四边形AnBn∁nDn的面积是ab2n+1，故④正确．
综上所述：正确的有①③④．
所以选：C．
30．已知：在四边形ABCD中，E、F、G、H分别是BC、AD、BD、AC的中点．
①求证：EF与GH互相平分；
②当四边形ABCD的边满足 AB＝CD 条件时，EF⊥GH．
试题分析：（1）连接GE、GF、HF、EH，根据三角形的中位线定理即可证得EG＝FH，GF＝EH，则四边形EHFG是平行四边形，利用平行四边形的性质即可证得；
（2）EF⊥GH时能得到四边形EHFG四边相等，从而得到四边形ABCD的四边相等．
答案详解：解：（1）连接GE、GF、HF、EH．
∵E、G分别是BC、BD的中点，
∴EG=12CD，
同理FH=12CD，FG=12AB，EH=12AB
∴EG＝FH、GF＝EH
∴四边形EHFG是平行四边形．
∴EF与GH互相平分；
（2）当EF⊥GH时，四边形EHFG是菱形，
此时GF＝FH＝HE＝EG，
∵EG=12CD，FH=12CD，FG=12AB，EH=12AB
∴AB＝CD，
∴当四边形ABCD的边满足条件AB＝CD时，EF⊥GH．