


- 专题04 易错题精选04之最值专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 1 次下载
- 专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题07 易错题集锦07之二次根式专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题08 选择压轴题精选-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
- 专题09 压轴大题精选01之动点专练-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版) 试卷 0 次下载
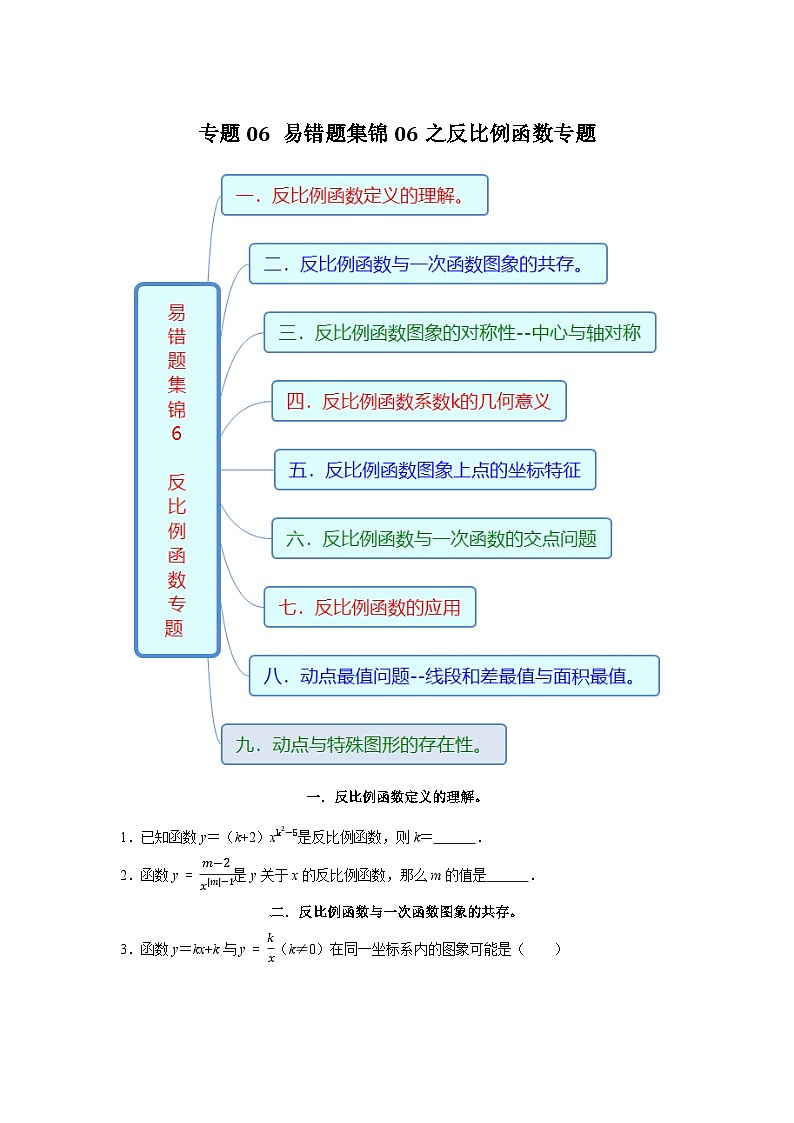
专题06 易错题集锦06之反比例函数专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版)
展开一.反比例函数定义的理解。
1.已知函数y=(k+2)xk2−5是反比例函数,则k= 2 .
试题分析:根据反比例函数的定义得到k2﹣5=﹣1且k+2≠0.
答案详解:解:∵函数y=(k+2)xk2−5为反比例函数,
∴k2﹣5=﹣1且k+2≠0.
解得k=2.
所以答案是:2.
2.函数y=m−2x|m|−1是y关于x的反比例函数,那么m的值是 ﹣2 .
试题分析:根据反比例函数的定义.即y=kx(k≠0).只需令|m|﹣1=1、m﹣2≠0即可.
答案详解:解:由题意,得|m|﹣1=1、m﹣2≠0.
解得m=﹣2.
所以答案是:﹣2.
二.反比例函数与一次函数图象的共存。
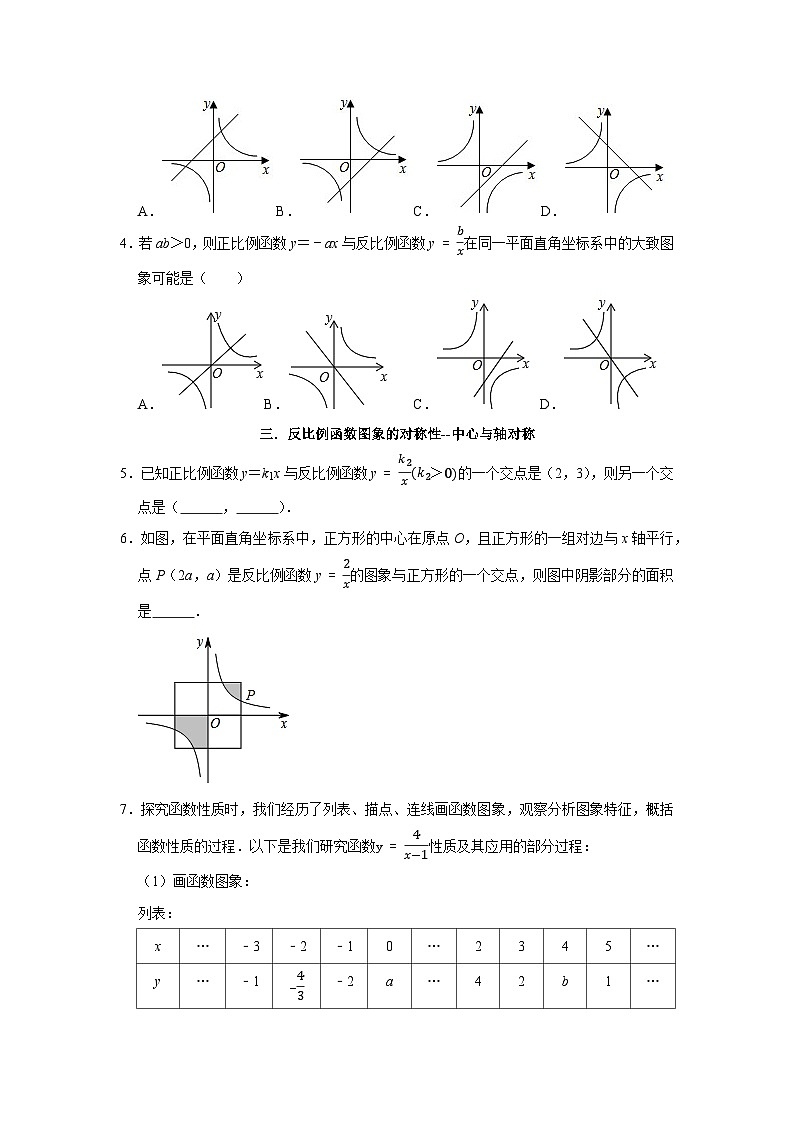
3.函数y=kx+k与y=kx(k≠0)在同一坐标系内的图象可能是( )
A.B.C.D.
试题分析:分两种情况讨论,当k>0时,分析出一次函数和反比例函数所过象限;再分析出k<0时,一次函数和反比例函数所过象限,符合题意者即为正确答案.
答案详解:解:①当k>0时,y=kx+k过一、二、三象限;y=kx过一、三象限;
②当k<0时,y=kx+k过二、三、四象象限;y=kx过二、四象限.
观察图形可知只有A符合①.
所以选:A.
4.若ab>0,则正比例函数y=﹣ax与反比例函数y=bx在同一平面直角坐标系中的大致图象可能是( )
A.B.C.D.
试题分析:根据ab>0及正比例函数与反比例函数图象的特点,可以从a>0,b>0和a<0,b<0两方面分类讨论得出答案.
答案详解:解:∵ab>0,∴分两种情况:
(1)当a>0,b>0时,正比例函数y=﹣ax的图象过原点、第二、四象限,反比例函数y=bx图象在第一、三象限,故B选项正确;
(2)当a<0,b<0时,正比例函数y=﹣ax的图象过原点、第一、三象限,反比例函数y=bx图象在第二、四象限,无选项符合.
所以选:B.
三.反比例函数图象的对称性--中心与轴对称
5.已知正比例函数y=k1x与反比例函数y=k2x(k2>0)的一个交点是(2,3),则另一个交点是( ﹣2 , ﹣3 ).
试题分析:此题可直接将坐标代入函数解析式,再联立解方程即可求出另一个交点.
答案详解:解:正比例函数y=k1x①与反比例函数y=k2x(k2>0)②的一个交点是(2,3),
∴将(2,3)代入①得k1=32,代入②得k2=6,即正比例函数y=32x③,反比例函数y=6x④,
∴32x=6x,解之得x=±2,把x=﹣2代入③得y=﹣3.
∴另一个交点是(﹣2,﹣3).
所以答案是:﹣2;﹣3.
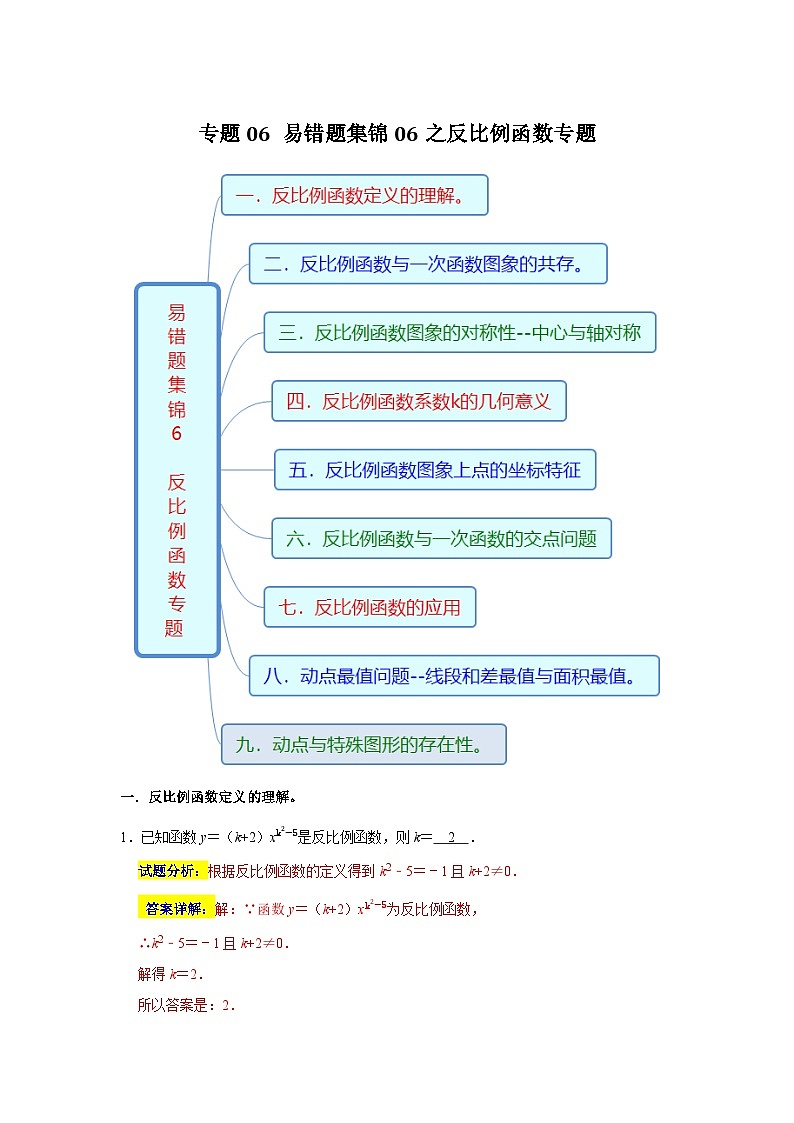
6.如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y=2x的图象与正方形的一个交点,则图中阴影部分的面积是 4 .
试题分析:先利用反比例函数解析式y=2x确定P点坐标为(2,1),由于正方形的中心在原点O,则正方形的面积为16,然后根据反比例函数图象关于原点中心对称得到阴影部分的面积为正方形面积的14.
答案详解:解:把P(2a,a)代入y=2x得2a•a=2,解得a=1或﹣1,
∵点P在第一象限,
∴a=1,
∴P点坐标为(2,1),
∴正方形的面积=4×4=16,
∴图中阴影部分的面积=14S正方形=4.
所以答案是4.
7.探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括函数性质的过程.以下是我们研究函数y=4x−1性质及其应用的部分过程:
(1)画函数图象:
列表:
直接写出上表中a,b的值:a= ﹣4 ;b= 43 ;并描点、连线得到函数图象:
(2)观察函数y=4x−1的图象,判断下列关于该函数性质的命题:
①该函数图象由两支曲线组成,两支曲线分别位于第一、三象限内;
②该函数图象既是中心对称图形,又是轴对称图形;
③y的值随x值的增大而减小;
④该函数最小值为﹣4,最大值为4.
其中错误的是 ①③④ ;(请写出所有错误命题的序号)
(3)结合图象,直接写出不等式4x−1>−1的解集: x>1或x<﹣3 .
试题分析:(1)将x=0,4分别代入解析式即可得a、b的值,再画出函数的图象;
(2)结合图象即可判断;
(3)根据图象求得即可.
答案详解:解:(1)把x=0代入y=4x−1得,y=﹣4;
把x=4代入y=4x−1得,y=43,
∴a=﹣4,b=43,
画出函数的图象如图:
,
所以答案是:﹣4,43;
(2)观察函数y=4x−1的图象,
①该函数图象由两支曲线组成,两支曲线分别位于第一、三、四象限内,故错误;
②该函数图象既是中心对称图形,又是轴对称图形,正确;
③在第一象限y的值随x值的增大而减小,在三四象限y的值随x值的增大而减小,故错误;
④该函数无最小值和最大值,故错误.
所以答案是:①③④;
(3)由图象可知:不等式4x−1>−1的解集为x>1或x<﹣3.
所以答案是:x>1或x<﹣3.
四.反比例函数系数k的几何意义
8.如图,过y轴正半轴上一点p,作x轴的平行线,分别与反比例函数y=nx和y=mx的图象交于点A、B,点C是x轴上任意一点,连接AC、BC,若△ABC的面积为3,则m﹣n的值为 6 .
试题分析:根据S△ABC=S△AOB=S△AOP+S△BOP,而S△AOP=−12n,S△BOP=12m,据此计算即可.
答案详解:解:∵直线AB∥x轴,
∴S△ABC=S△AOB=S△AOP+S△BOP=12|n|+12|m|=−12n+12m,
∵△ABC的面积为3,
∴12m−12n=3,
m﹣n=6,
所以答案是6.
9.如图,在x轴上方,平行于x轴的直线与反比例函数y=k1x和y=k2x的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1﹣k2= ﹣12 .
试题分析:根据AB∥x轴,设A(x,k1x),B(k2xk1,k1x)得到AB=k2xk1−x,根据△AOB的面积为6,列方程即可得到结论.
答案详解:解:∵AB∥x轴,
∴设A(x,k1x),B(k2xk1,k1x)
∴AB=k2xk1−x,
∵△AOB的面积为6,
∴12(k2xk1−x)•k1x=6,
∴k1﹣k2=﹣12,
解法二:设AB交y轴于点C.
由题意,△AOC的面积+△BOC的面积=6,
∴|k1|2+k22=6,
∵k1<0,
∴﹣k1+k2=12,
∴k1﹣k2=﹣12.
所以答案是:﹣12.
10.对于反比例函数y=k2+1x,下列说法正确的个数是( )
①函数图象位于第一、三象限;
②函数值y随x的增大而减小
③若A(﹣1,y1),B(2,y2),C(1,y3)是图象上三个点,则y1<y3<y2;
④P为图象上任一点,过P作PQ⊥y轴于点Q,则△OPQ的面积是定值.
A.1个B.2个C.3个D.4个
试题分析:利用反比例函数的性质用排除法解答.
答案详解:解:反比例函数y=k2+1x,因为k2+1>0,根据反比例函数的性质它的图象分布在第一、三象限,在每个象限内,y随x的增大而减小,故①说法正确,②错误,
若A(﹣1,y1),B(2,y2),C(1,y3)是图象上三个点,则y1<0<y2<y3;故说法③错误;
P为图象上任一点,过P作PQ⊥y轴于点Q,则△OPQ的面积为12(k2+1),故④说法正确;
所以选:B.
五.反比例函数图象上点的坐标特征
11.已知(﹣1,y1),(2,y2),(3,y3)在反比例函数y=−k2−1x的图象上,则函数值y1,y2,y3的从大到小的关系是 y1>y3>y2 .
试题分析:根据反比例函数的性质得到反比例函数图象分布在第二、四象限,在每一象限y随x的增大而增大,所以y1>0,y2<y3<0,从而得到它们的大小关系.
答案详解:解:∵﹣k2﹣1<0,
∴反比例函数图象分布在第二、四象限,在每一象限y随x的增大而增大,
∴y1>0,y2<y3<0,
∴y2<y3<y1.
所以答案是y1>y3>y2.
12.若点(x1,y1)、(x2,y2)和(x3,y3)分别在反比例函数y=−2x的图象上,且x1<x2<0<x3,则y1,y2,y3的大小关系是 y3<y1<y2 .
试题分析:根据k=﹣2<0,在每个象限内,y随x的增大而增大判断y1与y2的大小以及y3的符号,判断即可.
答案详解:解:∵k=﹣2,
∴x1<x2<0时,0<y1<y2,
∵x3,>0,
∴y3<0,
∴y3<y1<y2,
所以答案是:y3<y1<y2.
六.反比例函数与一次函数的交点问题
13.设函数y=3x与y=﹣2x﹣6的图象的交点坐标为(a,b),则1a+2b的值是 ﹣2 .
试题分析:由两函数的交点坐标为(a,b),将x=a,y=b代入反比例解析式,求出ab的值,代入一次函数解析式,得出2a+b的值,将所求式子通分并利用同分母分式的加法法则计算后,把ab及2a+b的值代入即可求出值.
答案详解:解:∵函数y=3x与y=﹣2x﹣6的图象的交点坐标是(a,b),
∴将x=a,y=b代入反比例解析式得:b=3a,即ab=3,
代入一次函数解析式得:b=﹣2a﹣6,即2a+b=﹣6,
则1a+2b=2a+bab=−63=−2,
所以答案是:﹣2.
14.如图,一次函数y=k1x+b与x轴交于点A,与反比例函数y=k2x相交于B、C两点,过点C作CD垂直于x轴,垂足为D,若点C的横坐标为2,OA=OD,△COD的面积为4.
(1)求反比例函数和一次函数的关系式;
(2)根据所给条件,请直接写出不等式k1x+b≤k2x的解集;
(3)若点P(x1,y1),Q(x2,2)是函数y=k2x图象上两点,且x1>x2,求y1的取值范围(直接写出结果).
试题分析:(1)根据三角形面积求出CD,得出C的坐标,把C的坐标代入反比例函数解析式,即可求出反比例函数的解析式,求出OA,得出A的坐标,把A、C的坐标代入一次函数的解析式,求出一次函数的解析式即可;
(2)根据C和B的坐标(﹣4,2),结合图象得出即可;
(3)根据已知和图象得出即可.
答案详解:解:(1)∵△COD的面积为4,点C的横坐标为2,
∴12×2×CD=4,
∴CD=4,
∴C的坐标为(2,﹣4),
把C的坐标代入反比例函数y=k2x得:k2=﹣8,
∴反比例函数的解析式是y=−8x;
∵OA=OD,OD=2,
∴AO=2,
∴A点坐标为(﹣2,0),
把A、C的坐标代入一次函数y=k1x+b得:=−2k1+b−4=2k1+b,
∴k1=﹣1,b=﹣2,
∴一次函数的解析式是y=﹣x﹣2;
(2)不等式k1x+b≤k2x的解集是﹣4≤x<0或x≥2;
(3)点P(x1,y1),Q(x2,2)是函数y=k2x图象上两点,且x1>x2,则y1的取值范围是y1>2或y1<0.
七.反比例函数的应用
15.如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为xm,DC的长为ym.
(1)求y与x之间的函数关系式;
(2)根据实际情况,对于(1)式中的函数自变量x能否取值为4m,若能,求出y的值,若不能,请说明理由;
(3)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
试题分析:(1)根据面积为60m2,可得出y与x之间的函数关系式;
(2)直接把x=4代入得出y的值进而比较即可;
(3)由(1)的关系式,结合x、y都是正整数,可得出x的可能值,再由三边材料总长不超过26m,DC的长<12,可得出x、y的值,继而得出可行的方案.
答案详解:解:(1)由题意得,S矩形ABCD=AD×DC=xy,
故y=60x.(x≥5)
(2)不能.当x=4时,y=15>12,不合题意;
(3)由y=60x,且x、y都是正整数,
可得x可取1,2,3,4,5,6,10,12,15,20,30,60,
∵2x+y≤26,0<y≤12,
∴符合条件的围建方案为:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.
16.喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
试题分析:(1)将D点的坐标代入反比例函数的一般形式利用待定系数法确定反比例函数的解析式,然后求得点C和点B的坐标,从而用待定系数法确定一次函数的解析式;
(2)将y=80代入反比例函数的解析式,从而求得答案.
答案详解:解:(1)停止加热时,设y=kx,
由题意得:50=k18,
解得:k=900,
∴y=900x,
当y=100时,解得:x=9,
∴C点坐标为(9,100),
∴B点坐标为(8,100),
当加热烧水时,设y=ax+20,
由题意得:100=8a+20,
解得:a=10,
∴当加热烧水,函数关系式为y=10x+20(0≤x≤8);
当停止加热,得y与x的函数关系式为y=100(8<x≤9);y=900x(9<x≤45);
(2)把y=80代入y=900x,得x=11.25,
因此从烧水开到泡茶需要等待3.25分钟.
八.动点最值问题--线段和差最值与面积最值。
17.如图,直线AB与反比例函数y=kx(x>0)的图象交于A,B两点,已知点A的坐标为(6,1),△AOB的面积为8.
(1)填空:反比例函数的关系式为 y=6x ;
(2)求直线AB的函数关系式;
(3)动点P在y轴上运动,当线段PA与PB之差最大时,求点P的坐标.
试题分析:(1)将点A坐标(6,1)代入反比例函数解析式y=kx,求出k的值即可;
(2)过点A作AC⊥x轴于点C,过B作BD⊥y轴于D,延长CA,DB交于点E,则四边形ODEC是矩形,设B(m,n),根据△AOB的面积为8,得3n−12m=8,得方程3n2﹣8n﹣3=0,解出可得B的坐标,利用待定系数法可得AB的解析式;
(3)如图,根据“三角形两边之差小于第三边”可知:当点P为直线AB与y轴的交点时,PA﹣PB有最大值是AB,可解答.
答案详解:解:(1)将点A坐标(6,1)代入反比例函数解析式y=kx,
得k=1×6=6,
则y=6x,
所以答案是:y=6x;
(2)过点A作AC⊥x轴于点C,过B作BD⊥y轴于D,延长CA,DB交于点E,则四边形ODEC是矩形,
设B(m,n),
∴mn=6,
∴BE=DE﹣BD=6﹣m,AE=CE﹣AC=n﹣1,
∴S△ABE=12AE⋅BE=12(n−1)(6−m),
∵A、B两点均在反比例函数y=kx(x>0)的图象上,
∴S△BOD=S△AOC=12×6×1=3,
∴S△AOB=S矩形ODEC﹣S△AOC﹣S△BOD﹣S△ABE=6n﹣3﹣3−12(n−1)(6−m)=3n−12m,
∵△AOB的面积为8,
∴3n−12m=8,
∴m=6n﹣16,
∵mn=6,
∴3n2﹣8n﹣3=0,
解得:n=3或−13(舍),
∴m=2,
∴B(2,3),
设直线AB的解析式为:y=kx+b,
则6k+b=12k+b=3,解得:k=−12b=4,
∴直线AB的解析式为:y=−12x+4;
(3)如图,根据“三角形两边之差小于第三边”可知:
当点P为直线AB与y轴的交点时,PA﹣PB有最大值是AB,
把x=0代入y=−12x+4中,得:y=4,
∴P(0,4).
18.如图,一次函数y=﹣x+b与反比例函数y=kx(x>0,k≠0)的图象交于点A(m,3)和B(3,1).
(1)填空:一次函数的表达式为 y=﹣x+4 ,反比例函数的表达式为 y=3x ;
(2)点P是线段AB上一点,过点P作PD⊥x轴于点D,连接OP,若△POD的面积为S,求S的最大值和最小值.
试题分析:(1)将点A的坐标分别代入一次函数y=﹣x+b与反比例函数y=kx(x>0),即可求解;
(2)S=12×OD×PD=12×n×(﹣n+4)=−12(n﹣2)2+2,根据1≤n≤3,即可求解.
答案详解:解:(1)将点A的坐标分别代入一次函数y=﹣x+b与反比例函数y=kx(x>0)并解得:b=4,k=3,
故一次函数与反比例函数的表达式分别为:y=﹣x+4,y=3x,
所以答案是:y=﹣x+4,y=3x;
(2)将点B的坐标代入反比例函数表达式并解得:m=1,即点B(3,1),
设点P(n,﹣n+4)(1≤n≤3),
S=12×OD×PD=12×n×(﹣n+4)=−12(n﹣2)2+2,
∵−12<0且1≤n≤3,
∴当n=2时,S取得最大值为2;
当n=1或3时,S取得最小值为32.
19.如图,在矩形ABCO中,AB=2,BC=4,点D是边AB的中点,反比例函数y1=kx(x>0)的图象经过点D,交BC于点E.
(1)求k的值及直线DE的解析式;
(2)在x轴上找一点P,使△PDE的周长最小,求此时点P的坐标;
(3)在(2)的条件下,求△PDE的面积.
试题分析:(1)根据矩形的性质可求出点B,点D的坐标,将点D的坐标代入反比例函数关系式可求出k的值,进而确定点E的坐标,再根据待定系数法求出直线DE的关系式即可;
(2)求出点D关于x轴的对称点D′的坐标,求出直线ED′与x轴的交点即可满足△PDE的周长最小;
(3)根据S△PDE=S梯形ABEP﹣S△BDE﹣S△ADP进行计算即可.
答案详解:解:(1)∵在矩形ABCO中,AB=2,BC=4,
∴点B(4,2),
∵点D是边AB的中点,
∴点D(4,1),
∵反比例函数y1=kx(x>0)的图象经过点D,
∴k=4×1=4,
∴反比例函数的关系式为y=4x,
当y=2时,即2=4x,
解得x=2,
∴点E(2,2),
设直线DE的关系式为y=kx+b,则
2k+b=24k+b=1,
解得,k=−12b=3,
∴直线DE的关系式为y=−12x+3;
(2)点D(4,1)关于x轴的对称点D′的坐标为(4,﹣1),
直线ED′与x轴的交点即为所求的点P,此时△PDE的周长最小,
设直线ED′的关系式为y=ax+c,则
2k+b=24k+b=−1,
解得k=−32b=5,
∴直线ED′的关系式为y=−32x+5,
当y=0时,即−32x+5=0,
解得x=103,
∴直线ED′与x轴的交点P(103,0),
∴当△PDE的周长最小时,点P(103,0);
(3)如图,
S△PDE=S梯形ABEP﹣S△BDE﹣S△ADP
=12(AP+EB)•AB−12BE•BD−12AP•AD
=12(4−103+2)×2−12×2×1−12(4−103)×1
=43,
答:△PDE的面积为43.
20.如图,一次函数y=x+4的图象与y轴交于点C,与反比例函数y=kx的图象交于B(﹣1,m),A(n,1)两点.
(1)求A、B两点的坐标和反比例函数的表达式;
(2)连接OA、OB,求△OAB的面积;
(3)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
试题分析:(1)把A(﹣1,m)、B(n,1)两点的坐标代入一次函数的解析式即可求出m、n的值,再把A的坐标代入反比例函数的解析式即可求出k的值;
(2)求得C的坐标,然后根据S△AOB=S△AOC﹣S△BOC求得即可;
(3)作B点关于x轴的对称点B′,连接AB′交x轴于P点,则B′(﹣1,﹣3),利用两点之间线段最短可判断此时PA+PB的值最小,再利用待定系数法求出直线AB′的解析式,然后求出直线与x轴的交点坐标即可得到P点坐标.
答案详解:解:(1)把B(﹣1,m)、A(n,1)两点的坐标代入y=x+4,
得m=﹣1+4=3,n+4=1,n=﹣3,
则B(﹣1,3)、A(﹣3,1).
把A(﹣3,1)代入y=kx,得k=﹣3×1=﹣3,
∴反比例函数的表达式为y=−3x;
(2)∵一次函数y=x+4的图象与y轴交于点C,
∴C(0,4),OC=4,
∵B(﹣1,3)、A(﹣3,1),
∴S△AOB=S△AOC﹣S△BOC=12×4×3−12×4×1=4;
(3)作B点关于x轴的对称点B′,连接AB′交x轴于P点,则B'(﹣1,﹣3),
∵PA+PB=PB'+PA=AB',
∴此时PA+PB的值最小,
设直线AB'的解析式为y=mx+n,
把点B'(﹣1,﹣3),A(﹣3,1)的坐标代入y=mx+n,得−m+n=−3−3m+n=1,
解得m=−2n=−5,
∴直线ab'的解析式为y=﹣2x﹣5,
当y=0时,x=−52,
∴点P的坐标为(−52,0).
九.动点与特殊图形的存在性。
21.如图1,已知点A(a,0),B(0,b),且a、b满足a+1+(a+b+3)2=0,平行四边形ABCD的边AD与y轴交于点E,且E为AD中点,双曲线y=kx经过C、D两点.
(1)a= ﹣1 ,b= ﹣2 ;
(2)求反比例函数表达式;
(3)点P在双曲线y=kx上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,直接写出满足要求的所有点Q的坐标;
(4)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,MNHT的值是否发生改变?若改变,直接写出其变化范围;若不改变,请直接写出其值.
试题分析:(1)先根据非负数的性质求出a、b的值;
(2)故可得出A、B两点的坐标,设D(1,t),由DC∥AB,可知C(2,t﹣2),再根据反比例函数的性质求出t的值即可;
(3)由(2)知k=4可知反比例函数的解析式为y=4x,再由点P在双曲线y=4x上,点Q在y轴上,设Q(0,y),P(x,4x),再分以AB为边和以AB为对角线两种情况求出x的值,故可得出P、Q的坐标;
(4)连NH、NT、NF,易证NF=NH=NT,故∠NTF=∠NFT=∠AHN,∠TNH=∠TAH=90°,MN=12HT由此即可得出结论.
答案详解:解:(1)∵a、b满足a+1+(a+b+3)2=0,
则a+1=0a+b+3=0,解得a=−1b=−2,
所以答案是:﹣1;﹣2;
(2)∴A(﹣1,0),B(0,﹣2),
∵E为AD中点,
∴xD=1,
设D(1,t),
又∵四边形ABCD是平行四边形,
∴C(2,t﹣2).
∴t=2t﹣4.
∴t=4.
∴D(1,4),
∵D(1,4)在双曲线y=kx上,
∴k=xy=1×4=4.
∴反比例函数的解析式为y=4x;
(3)∵点P在双曲线y=4x上,点Q在y轴上,
∴设Q(0,y),P(x,4x),
①当AB为边时:如图1所示:
若ABPQ为平行四边形,则−1+x2=0,解得x=1,此时P1(1,4),Q1(0,6);
如图2所示:
若ABQP为平行四边形,则−12=12x,解得x=﹣1,此时P2(﹣1,﹣4),Q2(0,﹣6);
②如图3所示:
当AB为对角线时:AP=BQ,且AP∥BQ;
∴−12=x2,解得x=﹣1,
∴P3(﹣1,﹣4),Q3(0,2);
综上所述,Q1(0,6);Q2(0,﹣6);Q3(0,2);
(4)如图4,连接NH、NT、NF,
∵MN是线段HT的垂直平分线,
∴NT=NH,
∵四边形AFBH是正方形,
∴∠ABF=∠ABH,
在△BFN与△BHN中,BF=BH,∠ABF=∠ABH,BN=BN,
∴△BFN≌△BHN(SAS),
∴NF=NH=NT,
∴∠NTF=∠NFT=∠AHN,
四边形ATNH中,∠ATN+∠NTF=180°,而∠NTF=∠NFT=∠AHN,
所以,∠ATN+∠AHN=180°,
因为四边形ATNH内角和为360°,
所以∠TNH=360°﹣180°﹣90°=90°.
∴MN=12HT,
∴MNHT=12.
即MNHT为定值,等于12.
22.如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数的图象相交于点A、B,点A的坐标为(2,3),点B的横坐标为6.
(1)求反比例函数与一次函数的解析式;
(2)如果点C、D分别在x轴、y轴上,四边形ABCD是平行四边形,求直线CD的表达式.
试题分析:(1)根据点A(2,3)在y=kx的图象上,得到3=k2,k=6,求出反比例函数的解析式为y=6x,求出点B的坐标为(6,1),把点A(2,3),B(6,1)代入y=kx+b即可得到结果;
(2)根据两点间的距离公式得到AB的长=(6−2)2+(1−3)2=25,由于四边形ABCD是平行四边形,得到AB∥CD,AB=CD=25,直线CD的解析式可设为y=−12x+n,求得D点坐标为(0,n),C点坐标为(2n,0),根据勾股定理列方程得到n=2或﹣2,即可得到结论.
答案详解:解:(1)∵点A(2,3)在y=kx的图象上,
∴3=k2,k=6.∴反比例函数的解析式为y=6x
把x=6代入上式得:y=1,
即点B的坐标为(6,1),
∵点A(2,3),B(6,1)在y=kx+b的图象上,
∴3=2k+b1=6k+b,
解得k=−12b=4.
∴一次函数的解析式为y=−12x+4;
(2)∵一次函数的解析式为y=−12x+4,
AB的长=(6−2)2+(1−3)2=25,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=25,
直线CD的解析式可设为y=−12x+n,
则D点坐标为(0,n),C点坐标为(2n,0),
在Rt△ODC中,OD2+OC2=DC2,
∴n2+(2n)2=20,解得n=2或﹣2(舍去),
∴直线CD的函数关系式为y=−12x+2.x
…
﹣3
﹣2
﹣1
0
…
2
3
4
5
…
y
…
﹣1
−43
﹣2
a
…
4
2
b
1
…
专题07 易错题集锦07之二次根式专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题07 易错题集锦07之二次根式专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题07易错题集锦07之二次根式专题原卷版docx、专题07易错题集锦07之二次根式专题解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题05 易错题精选05之分式方程及应用专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题05易错题精选05之分式方程及应用专题原卷版docx、专题05易错题精选05之分式方程及应用专题解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
专题04 易错题精选04之最值专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版): 这是一份专题04 易错题精选04之最值专题-2023-2024学年八年级数学下学期期末复习培优拔高(苏科版),文件包含专题04易错题精选04之最值专题原卷版docx、专题04易错题精选04之最值专题解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。












