专题09 压轴大题精选01之动点专练-2023-2024学年八年级数学下学期期末复习培优拔高（苏科版）

这是一份专题09 压轴大题精选01之动点专练-2023-2024学年八年级数学下学期期末复习培优拔高（苏科版），文件包含专题09压轴大题精选01之动点专练原卷版docx、专题09压轴大题精选01之动点专练解析版docx等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。
1．如图1，在平面直角坐标系中，矩形OABC的顶点A在y轴上，顶点C在x轴上．已知点A（0，m），C（n，0），且m、n是关于x的方程x2﹣6x+8＝0的两个根（m＜n）．点D是OC的中点，连接AD．
（1）求点B的坐标；
（2）若反比例函数y=kx（k≠0）的图象经过点B，点Q为y轴上一点，点P为反比例函数图象上一点，是否存在点Q，使以P，Q，A，D为顶点的四边形是平行四边形？若存在，请求出Q点的坐标；若不存在，请说明理由；
（3）如图2，若反比例函数y=kx（k≠0）的图象恰好与四边形ABCD的边有两个交点，则k的取值范围是 1＜k＜8 ．
试题分析：（1）解方程x2﹣6x+8＝0，得出m和n的值，可得点B的坐标；
（2）首先求出点D的坐标和反比例解析式，再分AD为边和对角线，分别画出图形，从而得到点Q的坐标；
（3）首先求出当直线AD与双曲线只有有个交点时k的值，从而得出k的范围．
答案详解：解：（1）∵m、n是关于x的方程x2﹣6x+8＝0的两个根，
∴m＝2，n＝4，
∴OA＝2，OC＝4，
∵四边形OABC是矩形，
∴B（4，2）；
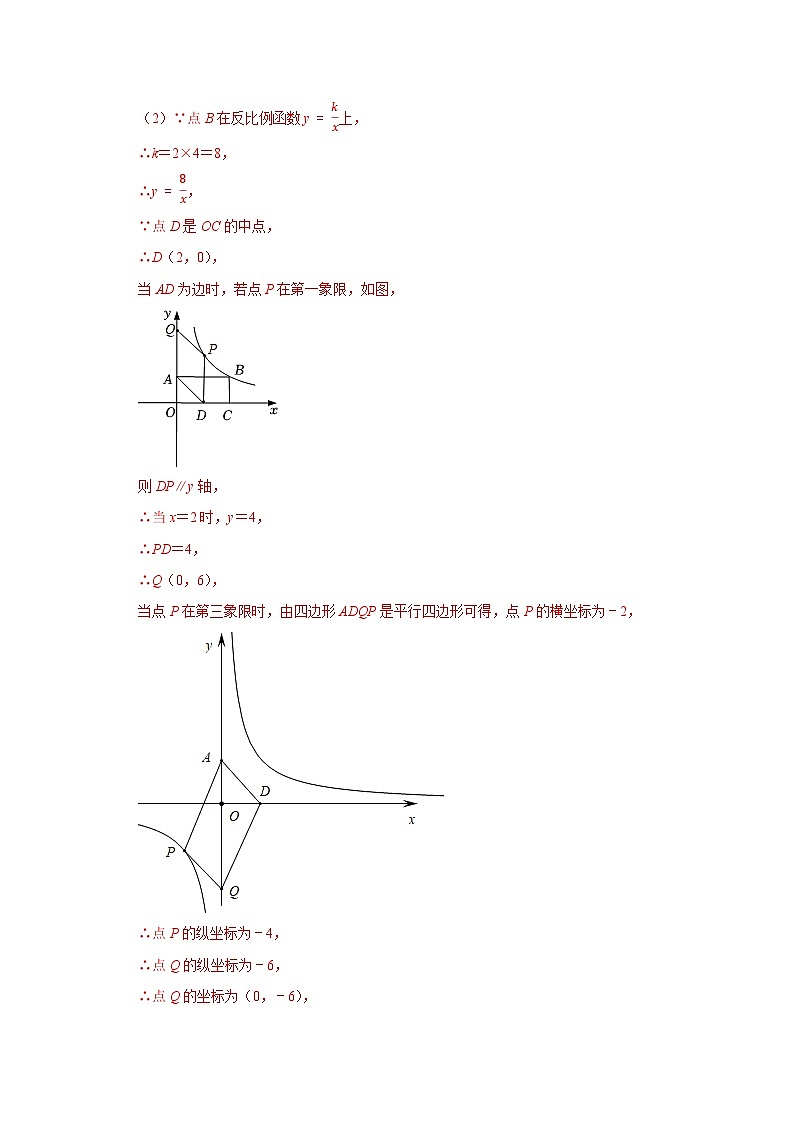
（2）∵点B在反比例函数y=kx上，
∴k＝2×4＝8，
∴y=8x，
∵点D是OC的中点，
∴D（2，0），
当AD为边时，若点P在第一象限，如图，
则DP∥y轴，
∴当x＝2时，y＝4，
∴PD＝4，
∴Q（0，6），
当点P在第三象限时，由四边形ADQP是平行四边形可得，点P的横坐标为﹣2，
∴点P的纵坐标为﹣4，
∴点Q的纵坐标为﹣6，
∴点Q的坐标为（0，﹣6），
当AD为对角线时，如图，点P（2，4），
∴AQ＝PD＝4，
∴Q（0，﹣2），
综上：Q（0，6）或（0，﹣6）或（0，﹣2）；
（3）由题意知，直线AD的解析式为y＝﹣x+2，
当y=kx（k≠0）的图象与直线AD恰好有一个交点时，则﹣x+2=kx，
∴x2﹣2x+k＝0，
∴Δ＝4﹣4k＝0，
∴k＝1，
∴反比例函数y=kx（k≠0）的图象恰好与四边形ABCD的边有两个交点时，1＜k＜8，
所以答案是：1＜k＜8．
2．如图1，四边形ABCD为正方形，点A在y轴上，点B在x轴上，且OA＝6，OB＝3，反比例函数y=kx（k≠0）在第一象限的图象经过正方形的顶点C．
（1）求点C的坐标和反比例函数的表达式；
（2）如图2，将正方形ABCD沿x轴向右平移m个单位长度得到正方形A'B'C'D'，点A'恰好落在反比例函数的图象上，求此时点D'的坐标；
（3）在（2）的条件下，点P为x轴上一动点，平面内是否存在点Q，使以点O、A'、P、Q为顶点的四边形为菱形，若存在，请直接写出点Q的坐标，若不存在，请说明理由．
试题分析：（1）作CH⊥x轴于H，利用AAS证明△AOB≌△BHC，得BH＝OA＝6，CH＝OB＝3，可得点C的坐标，再将点C代入反比例函数解析式可得答案；
（2）由（1）同理可得，点D（6，9），根据A'的坐标求出m的值，再利用平移的性质可得D'的坐标；
（3）分OA'＝OP，A'O＝A'P，PA'＝PO三种情形，分别画出菱形，根据菱形的性质可得答案．
答案详解：解：（1）作CH⊥x轴于H，
∵四边形ABCD是正方形，
∴AB＝BC，∠ABC＝90°，
∴∠ABO+∠CBH＝90°，
∵∠ABO+∠OAB＝90°，
∴∠OAB＝∠CBH，
∴△AOB≌△BHC（AAS），
∴BH＝OA＝6，CH＝OB＝3，
∴C（9，3），
∵反比例函数y=kx（k≠0）在第一象限的图象经过正方形的顶点C．
∴k＝9×3＝27，
∴y=27x；
（2）由（1）同理可得，点D（6，9），
∵点A'恰好落在反比例函数的图象上，
∴当y＝6时，x=92，
∴m=92，
∴D'（6+92，9），即D'（212，9）；
（3）当OA'＝OP时，如图，
∵A'（92，6），
∴OA'=152，
∵四边形OPQA'是菱形，
∴A'Q∥OP，A'Q＝OP，
∴Q（12，6），
当点Q'在第二象限时，Q'（﹣3，6），
当A'O＝A'P时，如图，
则点A'与Q关于x轴对称，
∴Q（92，﹣6），
当PO＝PA'时，如图，设P（m，0），
则PO＝PA'，
∴m2＝（m−92）2+62，
解得m=254，
∴OP＝A'Q=254，
∴Q（−74，6），
综上：Q（12，6）或（﹣3，6）或（92，﹣6）或（−74，6）．
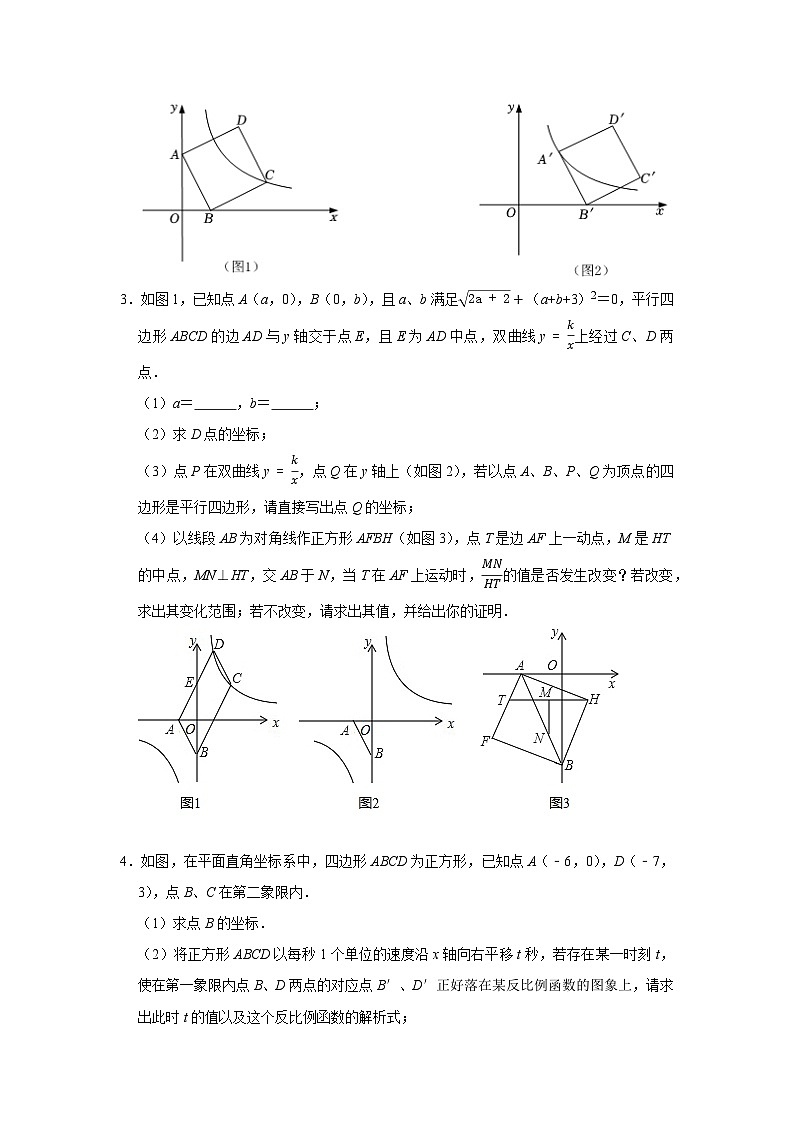
3．如图1，已知点A（a，0），B（0，b），且a、b满足2a+2+（a+b+3）2＝0，平行四边形ABCD的边AD与y轴交于点E，且E为AD中点，双曲线y=kx上经过C、D两点．
（1）a＝ ﹣1 ，b＝ ﹣2 ；
（2）求D点的坐标；
（3）点P在双曲线y=kx，点Q在y轴上（如图2），若以点A、B、P、Q为顶点的四边形是平行四边形，请直接写出点Q的坐标；
（4）以线段AB为对角线作正方形AFBH（如图3），点T是边AF上一动点，M是HT的中点，MN⊥HT，交AB于N，当T在AF上运动时，MNHT的值是否发生改变？若改变，求出其变化范围；若不改变，请求出其值，并给出你的证明．
试题分析：（1）先根据非负数的性质求出a、b的值，故可得出A、B两点的坐标，
（2）设D（1，t），由DC∥AB，可知C（2，t﹣2），再根据反比例函数的性质求出t的值即可；
（3）先求出k＝4可知反比例函数的解析式为y=4x，再由点P在双曲线y=kx上，点Q在y轴上，设Q（0，y），P（x，4x），再分以AB为边和以AB为对角线两种情况求出x的值，故可得出P、Q的坐标；
（4）连NH、NT、NF，易证NF＝NH＝NT，故∠NTF＝∠NFT＝∠AHN，∠TNH＝∠TAH＝90°，MN=12HT，由此即可得出结论．
答案详解：解：（1）∵2a+2+（a+b+3）2＝0，且2a+2≥0，（a+b+3）2≥0，
∴a+1=0a+b+3=0，
解得：a=−1b=−2，
所以答案是：﹣1，﹣2；
（2）由（1）知，a＝﹣1，b＝﹣2，
∴A（﹣1，0），B（0，﹣2），
∵E为AD中点，
∴xD＝1，
设D（1，t），
又∵四边形ABCD是平行四边形，
∴C（2，t﹣2），
∴t＝2t﹣4，
∴t＝4，
∴D（1，4）；
（3）由（2）知，D（1，4），
∴k＝4，
∴反比例函数的解析式为y=4x，
∵点P在双曲线y=kx上，点Q在y轴上，
∴设Q（0，y），P（x，4x），
①当AB为边时：
如图1所示：若ABPQ为平行四边形，则−1+x2=0，解得x＝1，此时P1（1，4），Q1（0，6）；
如图2所示；若ABQP为平行四边形，则−12=x2，解得x＝﹣1，此时P2（﹣1，﹣4），Q2（0，﹣6）；
②如图3所示；当AB为对角线时：AP＝BQ，且AP∥BQ；
∴−12=x2，解得x＝﹣1，
∴P3（﹣1，﹣4），Q3（0，2）；
故Q1（0，6）；Q2（0，﹣6）；Q3（0，2）；
（4）MNHT的值不变，为12；
理由：连NH、NT、NF，
∵MN是线段HT的垂直平分线，
∴NT＝NH，
∵四边形AFBH是正方形，
∴∠ABF＝∠ABH，
在△BFN与△BHN中，
BF=BH∠ABF=∠ABHBN=BN，
∴△BFN≌△BHN（SAS），
∴NF＝NH＝NT，
∴∠NTF＝∠NFT＝∠AHN，
在四边形ATNH中，∠ATN+∠NTF＝180°，
而∠NTF＝∠NFT＝∠AHN，
∴∠ATN+∠AHN＝180°，
在四边形ATNH中，∠TNH＝360°﹣180°﹣90°＝90°．
∴MN=12HT，
∴MNHT=12．
4．如图，在平面直角坐标系中，四边形ABCD为正方形，已知点A（﹣6，0），D（﹣7，3），点B、C在第二象限内．
（1）求点B的坐标．
（2）将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒，若存在某一时刻t，使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；
（3）在（2）的情况下，问是否存在x轴上的点P和反比例函数图象上的点Q，使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点P、Q的坐标；若不存在，请说明理由．
试题分析：（1）过点B作BE⊥x轴于点E，过点D作DF⊥x轴于点F，则△DAF≌△ABE，根据全等三角形的性质结合点A、D的坐标，即可求出点B的坐标；
（2）根据坐标的平移可找出点B′、D′的坐标，利用反比例函数图象上点的坐标特征可得出关于t的一元一次方程，解之即可得出t值，进而即可得出反比例函数的解析式；
（3）根据t的值可得出点B′、D′的坐标，设点P的坐标为（m，0），分B′D′为边及B′D′为对角线两种情况考虑：当B′D′为边时，根据平行四边形的性质结合点P在x轴上即可表示出点Q的坐标，再利用反比例函数图象上点的坐标特征即可求出m值，进而即可得出点P、Q的坐标；当B′D′为对角线时，根据平行四边形的对角线互相平分即可表示出点Q的坐标，再利用反比例函数图象上点的坐标特征即可求出m值，进而即可得出点P、Q的坐标．综上即可得出结论．
答案详解：解：（1）过点B作BE⊥x轴于点E，过点D作DF⊥x轴于点F，如图所示．
∵四边形ABCD为正方形，
∴∠BAD＝90°，AB＝DA，
∴∠BAE+∠DAF＝90°．
∵∠BAE+∠ABE＝90°，
∴∠DAF＝∠ABE．
在△DAF和△ABE中，∠AFD=∠BEA=90°∠ABE=∠DAFAB=DA，
∴△DAF≌△ABE（AAS），
∴DF＝AE，AF＝BE．
∵A（﹣6，0），D（﹣7，3），
∴AF＝BE＝1，DF＝AE＝3，
∴点B的坐标为（﹣3，1）．
（2）∵B（﹣3，1），D（﹣7，3），
∴B′（t﹣3，1），D′（t﹣7，3）．
∵点B′、D′在反比例函数的图象上，
∴t﹣3＝3（t﹣7），解得：t＝9，
∴t﹣3＝6，
∴反比例函数解析式为y=6x．
（3）∵t＝9，
∴B′（6，1），D′（2，3）．
∵点P在x轴上，
∴设点P的坐标为（m，0）．
分两种情况考虑：
当B′D′为边时，①∵四边形B′D′PQ为平行四边形，
∴点Q的坐标为（m+4，﹣2），
又∵点Q在反比例函数y=6x的图象上，
∴﹣8﹣2m＝6，解得：m＝﹣7，
∴点P的坐标为（﹣7，0），点Q的坐标为（﹣3，﹣2）；
②∵四边形B′D′QP为平行四边形，
∴点Q的坐标为（m﹣4，2），
又∵点Q在反比例函数y=6x的图象上，
∴2m﹣8＝6，解得：m＝7，
∴点P的坐标为（7，0），点Q的坐标为（3，2）；
当B′D′为对角线时，∵四边形B′QD′P为平行四边形，
∴点Q的坐标为（8﹣m，4），
又∵点Q在反比例函数y=6x的图象上，
∴32﹣4m＝6，解得：m=132，
∴点P的坐标为（132，0），点Q的坐标为（32，4）．
综上所述：存在点P、Q，使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形，P（﹣7，0）、Q（﹣3，﹣2）或P（7，0）、Q（3，2）或P（132，0）、Q（32，4）．
5．在矩形ABCD中，P是线段BC上的一个动点，将△ABP沿直线AP翻折，点B的对应点为E，直线PE与直线AD交于点F．
（1）如图①，当点F在AD的延长线上时，求证AF＝PF；
（2）若AB＝6，BC足够长，当点E到直线AD的距离等于3时，求BP的长；
（3）若AB＝6，BC＝10，当点P、E、D在同一直线上（如图②）时，点P开始向点C运动，到与C重合时停止，则点F运动的路程是 4.8 ．
试题分析：（1）由矩形的性质得AD∥BC，则∠APB＝∠PAF，由翻折的性质得∠APB＝∠APF，得出∠APF＝PAF，即可得出结论；
（2）①当点E在矩形ABCD内部时，过点E作HG∥AB，分别交AD、BC于H、G，延长PE交AD于F，则HG⊥AD，EH＝3，先证∠EAH＝30°，得出∠BAE＝60°，由折叠的性质得∠EAP＝∠BAP=12∠BAE＝30°，再由含30°角直角三角形的性质得AP＝2BP，在Rt△ABP中，由勾股定理即可求出BP的值；
②当点E在矩形ABCD外部时，过点E作EH∥AB，分别交AD于H，则EH⊥AD，EH＝3，先证∠EAH＝30°，由折叠的性质得∠EAP＝∠BAP=12∠BAE＝60°，则∠APB＝30°，再由含30°角直角三角形的性质得AP＝2AB，在Rt△ABP中，由勾股定理即可求出BP的值；
（3）由矩形的性质得AD∥BC，AB＝CD＝6，AD＝BC＝10，∠ADC＝90°，则∠DAC＝∠BCA，当点P、E、D在同一直线上时，点P开始向点C运动，开始点F沿DA方向移动，点E与点F重合后，点F又沿AD方向移动，则点F运动的路程为：DF′+F′F″，E′与F′重合时，DF′＝AD﹣AF′＝4，由折叠的性质得∠BCA＝∠E″CA，推出∠DAC＝∠E″CA，得出AF″＝CF″＝AD﹣DF″＝10﹣DF″，在Rt△CDF″中，由勾股定理求出DF″＝3.2，得出F′F″＝DF′﹣DF″＝0.8，即可得出结果．
答案详解：（1）证明：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠APB＝∠PAF，
由翻折的性质得：∠APB＝∠APF，
∴∠APF＝PAF，
∴AF＝PF；
（2）解：∵四边形ABCD是矩形，
∴∠B＝∠BAD＝90°，
①当点E在矩形ABCD内部时，过点E作HG∥AB，分别交AD、BC于H、G，延长PE交AD于F，如图③所示：
则HG⊥AD，EH＝3，
由翻折的性质得：AE＝AB＝6，
在Rt△AHE中，EH=12AE，
∴∠EAH＝30°，
∴∠BAE＝90°﹣∠EAH＝90°﹣30°＝60°，
由折叠的性质得：∠EAP＝∠BAP，
∴∠EAP＝∠BAP=12∠BAE=12×60°＝30°，
∴AP＝2BP，
在Rt△ABP中，由勾股定理得：AB2+BP2＝AP2，
即62+BP2＝（2BP）2，
解得：BP＝23（负值已舍去）；
②当点E在矩形ABCD外部时，过点E作EH∥AB，分别交AD于H，如图④所示：
则EH⊥AD，EH＝3，
由翻折的性质得：AE＝AB＝6，
在Rt△AHE中，EH=12AE，
∴∠EAH＝30°，
∴∠BAE＝90°+∠EAH＝90°+30°＝120°，
由折叠的性质得：∠EAP＝∠BAP，
∴∠EAP＝∠BAP=12∠BAE=12×120°＝60°，
∴∠APB＝90°﹣60°＝30°，
∴AP＝2AB＝12，
在Rt△ABP中，由勾股定理得：AB2+BP2＝AP2，
即62+BP2＝122，
解得：BP＝63（负值已舍去）；
综上所述，BP的长为23或63；
（3）解：∵四边形ABCD是矩形，
∴AD∥BC，AB＝CD＝6，AD＝BC＝10，∠ADC＝90°，
∴∠DAC＝∠BCA，
当点P、E、D在同一直线上时，点P开始向点C运动，开始点F沿DA方向移动，点E与点F重合后，点F又沿AD方向移动，如图②所示：
则点F运动的路程为：DF′+F′F″，
E′与F′重合时，由折叠的性质得：AF′＝AB＝6，
∴DF′＝AD﹣AF′＝10﹣6＝4，
由折叠的性质得：∠BCA＝∠E″CA，
∴∠DAC＝∠E″CA，
∴AF″＝CF″＝AD﹣DF″＝10﹣DF″，
在Rt△CDF″中，由勾股定理得：DF''2+CD2＝CF″2，
即DF″2+62＝（10﹣DF″）2，
解得：DF″＝3.2，
∴F′F″＝DF′﹣DF″＝4﹣3.2＝0.8，
∴DF′+F′F″＝4+0.8＝4.8，
所以答案是：4.8．
6．如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点B在反比例函数y=kx（k≠0）的第一象限内的图象上，OA＝4，OC＝3，动点P在x轴的上方，且满足S△PAO=13S矩形AOCB．
（1）若点P在这个反比例函数的图象上，求点P的坐标；
（2）连接PO、PA，求PO+PA的最小值；
（3）若点Q是平面内一点，使得以A、B、P、Q为顶点的四边形是菱形，则请你直接写出满足条件的所有点Q的坐标．
试题分析：（1）首先根据点B坐标，确定反比例函数的解析式，设点P的纵坐标为m（m＞0），根据S△PAO=13S矩形AOBC，构建方程即可解决问题；
（2）过点（0，2），作直线l⊥y轴．由（1）知，点P的纵坐标为2，推出点P在直线l上作点O关于直线l的对称点O′，则OO′＝4，连接AO′交直线l于点P，此时PO+PA的值最小；
（3）分四种情形分别求解即可解决问题；
答案详解：解：（1）∵四边形OABC是矩形，OA＝4，OC＝3，
∴点B的坐标为（4，3），
∵点B在反比例函数y=kx（k≠0）的第一象限内的图象上
∴k＝12，
∴y=12x，
设点P的纵坐标为m（m＞0），
∵S△PAO=13S矩形AOBC．
∴12•OA•m＝OA•OC•13，
∴m＝2，
当点，P在这个反比例函数图象上时，则2=12x，
∴x＝6
∴点P的坐标为（6，2）．
（2）过点（0，2），作直线l⊥y轴．
由（1）知，点P的纵坐标为2，
∴点P在直线l上
作点O关于直线l的对称点O′，则OO′＝4，
连接AO′交直线l于点P，此时PO+PA的值最小，
则PO+PA的最小值＝PO′+PA＝O′A=42+42=42．
（3）
①如图2中，当四边形ABQP是菱形时，易知AB＝AP＝PQ＝BQ＝3，P1（4−5，2），P2（4+5，2），
∴Q1（4−5，5），Q2（4+5，5）．
②如图3中，当四边形ABPQ是菱形时，P3（4﹣22，2），P4（4+22，2），
∴Q3（4﹣22，﹣1），Q4（4+22，﹣1）．
综上所述，点Q的坐标为Q1（4−5，5），Q2（4+5，5），Q3（4﹣22，﹣1），Q4（4+22，﹣1）．
7．如图，在平面直角坐标系中，四边形ABCO为矩形，B（5，4），D（﹣3，0），点P从点A出发，以每秒1cm的速度沿AB方向向终点B运动；点Q从点D出发，以每秒2cm的速度沿DC方向向终点C运动，已知动点P、Q同时出发，当点P、Q有一点到达终点时，P、Q都停止运动，设运动时间为t秒．
（1）用含t的代数式表示：BP＝ （5﹣t） cm，CQ＝ 3 cm；
（2）函数y=kx的图象在第一象限内的一支双曲线经过点P，且与线段BC交于点M，若△POM的面积为7.5cm2，试求此时t的值；
试题分析：（1）由题意得出AP＝tcm，AB＝5cm，即可得出BP；由DC＝8，DQ＝2t，即可得出CQ；当BP＝CQ时，四边形PQCB是矩形，得出方程，解方程即可求出t的值；
（2）由点P坐标得出k＝4t，得出BM，连接PO、PM、OM，△POM的面积＝矩形AOCB的面积﹣△AOP的面积﹣△PBM的面积﹣△OCM的面积，即可得出结果；
（3）由勾股定理得出PQ2＝（t﹣3）2+42，PC2＝（t﹣5）2+42，CQ2＝（8﹣2t）2，分情况讨论：①当PQ＝PC时；②当PQ＝CQ时；③当PC＝CQ时；分别解方程求出t的值，再求出AE即可得出点E的坐标．
答案详解：解：（1）根据题意得：AP＝tcm，AB＝5cm，
∴BP＝（5﹣t）cm，
∵DC＝DO+OC＝3+5＝8，DQ＝2tcm，
∴CQ＝DC﹣DQ＝（8﹣2t）cm，
所以答案是：（8﹣2t）；
当BP＝CQ时，四边形PQCB是矩形，
∴5﹣t＝8﹣2t，
解得：t＝3，
∴当t＝3时，四边形PQCB为矩形；
所以答案是：（5﹣t）；3；
（2）∵点P的坐标为（t，4），点P在反比例函数的图象上，
∴k＝4t，
∴y=4tx，
∴点M的坐标为（5，4t5），
∴BM＝4−4t5，
连接PM，如图1所示：
∴△POM的面积S＝矩形AOCB的面积﹣△AOP的面积﹣△PBM的面积﹣△OCM的面积
＝5×4−12×t×4−12×（5﹣t）×（4−4t5）−12×5×4t5=−25t2+10，
∵点Q从点D运动到点C用是为4秒，点P从点A运动到点B用时为5秒，
∴0≤t≤4，
∴S=−25t2+10（0≤t≤4），
根据题意可得，S=−25t2+10＝7.5，
解得t＝2.5（负值舍去），
∴若△POM的面积为7.5cm2，t的值为2.5；
8．将一个矩形纸片OABC放置在平面直角坐标系中，OA，OC分别在x轴，y轴的正半轴上，点B坐标为（4，10）．
（Ⅰ）如图①，将矩形纸片OABC折叠，使点B落在y轴上的点D处，折痕为线段AE，求点D坐标；
（Ⅱ）如图②，点E，F分别在OC，AB边上．将矩形纸片OABC沿线段EF折叠，使得点B与点D（0，2）重合，求点C的对应点G的坐标；
（Ⅲ）在（Ⅱ）的条件下，若点P是坐标系内任意一点，点Q在y轴上，使以点D，F，P，Q为顶点的四边形是菱形，请直接写出满足条件的点P的坐标．
试题分析：（Ⅰ）运用矩形性质和折叠性质及勾股定理即可求得答案；
（Ⅱ）过点G作GH⊥y轴于点H，由折叠知，四边形BCEF与四边形DGEF全等，由EG2+GD2＝ED2，建立方程求解即可；
（Ⅲ）设Q（0，y），P（m，n），根据点Q在y轴上，使以点D，F，P，Q为顶点的四边形是菱形，分三种情况：DQ＝DF或FQ＝DF或DQ＝FQ，运用勾股定理先求出点Q的坐标，再依据菱形性质求出对应的点P坐标．
答案详解：解：（Ⅰ）∵四边形OABC是矩形，
∴∠BAO＝∠BCO＝90°，OA＝CB，CO＝BA．
∵点B坐标为（4，10），
∴OA＝CB＝4，CO＝BA＝10；
由折叠可知，△ADE≌△ABE，
∴DA＝BA＝10．
在Rt△AOD中，OD=DA2−OA2=102−42=221，
∴点D的坐标为（0，221 ）；
（Ⅱ）如图，过点G作GH⊥y轴于点H，
∵点D （0，2），
∴DO＝2，
∵四边形OABC是矩形，
∴∠B＝90°；
由折叠知，四边形BCEF与四边形DGEF全等，
∴∠EGD＝∠B＝90°，GD＝CB＝4，CE＝EG．
设CE＝EG＝x，则ED＝CO﹣CE﹣DO＝10﹣2﹣x＝8﹣x．
在Rt△EGD中，EG2+GD2＝ED2，
∴x2+42＝（8﹣x）2，
解得：x＝3．
∴EG＝3，ED＝5．
∴S△EGD=12EG•GD=12ED•GH，
∴12×3×4=12×5×GH，
∴GH=125，
在Rt△GHD中，HD=GD2−GH2=42−(125)2=165，
∴HO＝HD+DO=165+2=265．
∴点G的坐标为（−125，265）．
（Ⅲ）由折叠可知，∠BFE＝∠DFE，
∵BF∥ED，
∴∠BFE＝∠FED，
∴∠FED＝∠DFE，
∴BF＝DF＝ED＝5，
∴AF＝AB﹣BF＝10﹣5＝5，
∴F（4，5），
设Q（0，y），P（m，n），
∵D （0，2），
∴DQ＝|y﹣2|，DF＝5，FQ2＝42+（y﹣5）2，DF的中点坐标为（2，72），
∵点Q在y轴上，使以点D，F，P，Q为顶点的四边形是菱形，
∴分三种情况：DQ＝DF或FQ＝DF或DQ＝FQ，
①当DQ＝DF时，|y﹣2|＝5，
解得：y＝7或﹣3，
∴Q（0，7）或（0，﹣3），
∴P（4，0）或（4，10），
②当FQ＝DF时，42+（y﹣5）2＝25，
解得y＝8或y＝2（舍去），
∴Q（0，8），
∴P（﹣4，5），
③当DQ＝FQ时，|y﹣2|2＝42+（y﹣5）2，
解得：y=376，
∴Q（0，376），
∵m+02=2，n+3762=72，
∴m＝4，n=56，
∴P（4，56），
综上所述，点P的坐标为（4，10），（4，0），（﹣4，5），（4，56）．
9．如图，在平面直角坐标系中，A（8，0）、B（0，6）是矩形OACB的两个顶点，双曲线y=kx（k≠0，x＞0）经过AC的中点D，点E是矩形OACB与双曲线y=kx的另一个交点．
（1）点D的坐标为 （8，3） ，点E的坐标为 （4，6） ；
（2）动点P在第一象限内，且满足S△POB=12S△ODE
①若点P在这个反比例函数的图象上，求点P的坐标；
②若点Q是平面内一点，使得以A、C、P、Q为顶点的四边形是菱形，请你直接写出满足条件的所有点Q的坐标．
试题分析：（1）根据矩形的性质得点C的坐标，再利用中点坐标公式得点D的坐标，从而得出k的值，再将y＝6代入即可；
（2）①首先根据S△ODE＝S梯形OACE﹣S△OAD﹣S△ECD，求出△ODE的面积，再根据S△PBO=12S△ODE．得出点P的横坐标，从而得出答案；
②由①知，点P在直线x＝3上，设直线x＝3交x轴于H，分AP＝AC，CA＝C，PA＝PC三种情形，分别利用菱形的性质可得答案．
答案详解：解：（1）∵四边形OACB是矩形，
∴AC＝OB＝6，
∴C（8，6），
∵点D是AC的中点，
∴D（8，3），
∴k＝8×3＝24，
∴y=24x，
当y＝6时，x＝4，
∴E（4，6），
所以答案是：（8，3），（4，6）；
（2）①由题意知，S△ODE＝S梯形OACE﹣S△OAD﹣S△ECD
=12×（4+8）×6−12×4×3−12×8×3
＝18，
∵S△PBO=12S△ODE．
∴12×6×xP=12×18，
∴xP＝3，
∴y＝8，
∴P的坐标为（3，8）；
②由①知，点P在直线x＝3上，设直线x＝3交x轴于H，
当AC＝AP＝6时，若点P在第一象限，
∴PH=62−52=11，
∴Q（3，11+6），
当点P在第四象限舍去，
当CA＝CP时，
同理得，Q（3，−11），Q'（3，11），
当PC＝PA时，点P（3，3），
则点Q与P关于AC对称，
∴Q（13，3），
综上，点Q（3，11+6）或（3，−11）或（3，11）或（13，3）．
10．已知结论：在直角三角形中，30°角所对的直角边是斜边的一半，请利用这个结论进行下列探究活动．如图，在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝2，D为AB中点，P从A点出发，沿AC以每秒1个单位长度的速度向C运动，设P点运动时间为t秒．连接PD，把△APD沿PD翻折得到△EPD，连接CE．
（1）当DE⊥AB时，t＝ 23−2 ．
（2）当以A、P、E、D为顶点的四边形是平行四边形时，求出t的值．
（3）在P点运动过程中，是否存在以B、C、E、D为顶点的四边形是平行四边形？若存在，请求出t的值；若不存在，请说明理由．
试题分析：（1）作PH⊥AB于H，利用解△APD，可得AP的长，从而得出答案；
（2）根据题意知，AP＝PE＝AD，从而求出t的值；
（3）分BD为边或BD为对角线，分别画出图形，利用含30°角的直角三角形的性质求出答案．
答案详解：解：（1）如图，作PH⊥AB于H，
在Rt△ABC中，∵∠A＝30°，
∴AB＝2BC＝4，
∵点D为AB的中点，
∴AD＝2，
∵DE⊥AB，
∴∠ADP＝∠EDP＝45°，
设PH＝DH＝x，则AH=3x，
∴x+3x＝2，
∴x=3−1，
∴PH=3−1，
∴AP＝2PH＝23−2；
（2）∵∠C＝90°，∠A＝30°，BC＝2，
∴AB＝2BC＝4，
∵D为AB中点，
∴AD=BD=12AB=2，
∵四边形ADEP是平行四边形，
∴AD∥PE，AD＝PE，
∵△APD沿PD翻折得到△EPD，
∴AP＝PE，
∴AP＝AD＝2，
∴t＝2；
（3）存在，理由如下：
①当BD为边时，∵∠A＝30°，∠ACB＝90°，
∴∠B＝60°，
∵四边形DBCE是平行四边形，
∴CE＝BD，CE∥BD，DE∥BC，
∴∠ECP＝∠A＝30°，∠CED＝∠ADE＝∠B＝60°，
∵△APD沿PD翻折得到△EPD，
∴∠ADP＝∠EDP＝30°，AP＝PE，
∴∠PAD＝∠PDA＝30°，
∴AP＝PD＝PE，
∴∠PED＝∠PDE＝30°，
∴∠PEC＝∠PED+∠DEC＝90°，
∵∠ECP＝30°，
∴PC＝2PE，
∴PC2＝PE2+EC2，即4PE2＝PE2+22，
解得：t=PA=PE=233；
②当BD为对角线时，∵BC＝BD＝AD，∠B＝60°，
∴△BCD都是等边三角形，
∴∠ACD＝30°，
∵四边形BCDE是平行四边形，
∴平行四边形BCDE为菱形，
∴DE＝DC＝AD，∠ADC＝∠CDE＝120°，
又∵CD＝CD，
∴△ACD≌△ECD（SAS），
∴AC＝CE，
∴△ECD是△ACD沿CD翻折得到，
∵△APD沿PD翻折得到△EPD，
∴点P与点C重合，
∴t=AP=AC=23；
故当t=233或t=23时，以B、C、E、D为顶点的四边形是平行四边形．
11．如图，在平行四边形ABCD中，∠BAC＝90°，∠B＝60°，AB＝6．动点P从点A出发沿AD以1cm/s速度向终点D运动，同时点Q从点C出发，以4cm/s速度沿射线CB运动，当点P到达终点时，点Q也随之停止运动，设点P运动的时间为t秒．
（1）当PQ⊥BC时，t＝ 95 ；
（2）请问是否存在t的值，使得A，B，P，Q为顶点的四边形为平行四边形？若存在，求出t的值；若不存在，请说明理由；
（3）若点P关于直线AQ对称的点恰好落在直线AB上，请求出t的值.
试题分析：（1）先证四边形AHQP是平行四边形，可得AP＝QH，列出方程可求解；
（2）分两种情况讨论，由平行四边形的性质可得AP＝BQ，列出方程可求解；
（3）分两种情况讨论，由轴对称的性质和等边三角形的性质可求解．
答案详解：解：（1）过点A作AH⊥BC于H，
∵四边形ABCD是平行四边形，∠BAC＝90°，∠ABC＝60°，
∴∠ACB＝30°，AD∥BC，∠DAB＝120°，
∴BC＝2AB＝12，AC＝63，
∵∠ACB＝30°，AH⊥BC，
∴AH=12AC＝33，CH＝9，
∵PQ⊥BC，AH⊥BC，
∴PQ∥AH，
又∵AD∥BC，
∴四边形AHQP是平行四边形，
∴AP＝QH，
∴t＝9﹣4t，
∴t=95，
所以答案是：95；
（2）存在，
当AB为边时，∵四边形ABQP是平行四边形，
∴AP＝BQ，
∴t＝12﹣4t，
∴t=125，
当AB为对角线时，∵四边形APBQ是平行四边形，
∴AP＝BQ，
∴t＝4t﹣12，
∴t＝4，
综上所述：t的值为125或4；
（3）如图，当点P的对称点在线段AB上时，
∴∠DAQ＝∠QAB＝60°，
∴∠QAB＝∠ABQ＝60°，
∴△ABQ是等边三角形，
∴AB＝BQ，
∴6＝12﹣4t，
∴t=32，
如图，当点P的对称点在线段BA的延长线上时，
∵∠DAB＝120°，
∴∠PAP'＝60°，
∵点P的对称点在线段BA的延长线上，
∴∠BAQ=12∠PAP'＝30°，
∵∠ABC＝∠BAQ+∠AQB，
∴∠BAQ＝∠AQB＝30°，
∴AB＝BQ＝6，
∴CQ＝12+6＝18，
∴4t＝18，
∴t=92，
综上所述：t的值为92或32．
12．在矩形ABCD中，AB＝5，AD＝4．
（1）将矩形ABCD折叠，使得顶点B落在CD边上的P处（如图1），折痕AO与边BC交于点O，连AP、OP、OA．求线段CO的长；
（2）在（1）的条件下，连BP（如图2）．动点M在线段AP上（与点P、A不重合），动点N在线段AB的延长线上，且BN＝PM，连MN交PB于点F，作ME⊥BP于点E．试问点M、N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；若不变，求出线段EF的长度．
试题分析：（1）根据矩形的性质以及折叠的性质可得AP＝5，根据勾股定理可得CP＝2，设CO＝x，在Rt△COP中根据勾股定理列方程，即可求出CO的长；
（2）过点M作MG∥AB，可得∠ABP＝∠MGP，易证AB＝AP，进一步可知△MPG是等腰三角形，根据等腰三角形的性质可得PE＝GE，再证明△GMF≌△BNF（AAS），可得GF＝FB，进一步可知EF=12PB，根据勾股定理求出PB的长，即可确定EF的长．
答案详解：解：（1）在矩形ABCD中，AB＝CD，AD＝BC，∠D＝∠C＝90°，
根据折叠，可得AP＝AB，OP＝OB，
∵AB＝5，AD＝4，
∴AP＝5，
在Rt△ADP中，根据勾股定理，得DP＝3，
∴CP＝2，
设CO＝x，
则OB＝4﹣x，
∴PO＝4﹣x，
在Rt△COP中，根据勾股定理，
得22+x2＝（4﹣x）2，
解得x=32，
∴CO=32；
（2）点M、N在移动过程中，线段EF的长度不变．
过点M作MG∥AB，如图所示：
则∠ABP＝∠MGP，∠MGF＝∠NBF，
根据折叠，可得AB＝AP，
∴∠APB＝∠ABP，
∴∠APB＝∠MGP，
∴MP＝MG，
∵ME⊥BP，
∴E是PG的中点，
∴PE＝GE，
∵PM＝BN，PM＝GM，
∴GM＝BN，
在△GMF和△BNF中，
∠MFG=∠NFB∠MGF=∠NBFGM=BN，
∴△GMF≌△BNF（AAS），
∴GF＝BF，
∴EF=12PB，
由（1）得PC＝2，BC＝4，
根据勾股定理，得PB=25，
∴EF=5．