专题24与圆有关的位置关系过关检测-备战2024年中考数学一轮复习考点

这是一份专题24与圆有关的位置关系过关检测-备战2024年中考数学一轮复习考点，文件包含专题24与圆有关的位置关系过关检测-备战2024年中考数学一轮复习考点帮教师版docx、专题24与圆有关的位置关系过关检测-备战2024年中考数学一轮复习考点帮考试版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
一、选择题（本题共10小题，每小题3分，共30分）。
1．若⊙O的半径为6cm，PO＝8cm，则点P与⊙O的位置关系是（ ）
A．点P在⊙O外B．点P在⊙O上C．点P在⊙O内D．不能确定
【答案】A
【解答】解：∵点P到圆心的距离8cm大于圆的半径6cm，
∴点P在圆外．
故选：A．
2．下列说法中，正确的是（ ）
A．弦的垂直平分线必经过圆心
B．三点确定一个圆
C．平分弦的直径垂直于这条弦
D．长度相等的弧是等弧
【答案】A
【解答】解：A、弦的垂直平分线必经过圆心，故本选项符合题意；
B、不在同一直线上的三点确定一个圆，故本选项不符合题意；
C、平分弦（非直径）的直径垂直这条弦，该选项说法错误，故此选项不符合题意；
D、在同圆或等圆中，能够互相重合的弧叫做等弧，长度相等的弧不一定能够重合，故本选项不符合题意．
故选：A．
3．如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠C＝50°，则∠B的大小等于（ ）
A．20°B．25°C．40°D．50°
【答案】A
【解答】解：连接OA，
∵AC是⊙O的切线，
∴∠OAC＝90°，
∵∠C＝50°，
∴∠AOC＝90°﹣50°＝40°，
∵OA＝OB，
∴∠B＝∠OAB，
∵∠AOC＝∠B+∠OAB＝40°，
∴∠B＝20°，
故选：A．
4．如图，PA、PB分别切⊙O于A、B，PA＝10，C是劣弧AB上的点（不与点A、B重合），过点C的切线分别交PA、PB于点E、F．则△PEF的周长为（ ）
A．10B．15C．20D．25
【答案】C
【解答】解：∵PA、PB分别切⊙O于A、B，
∴PB＝PA＝10cm，
∵EA与EC为⊙的切线，
∴EA＝EC，
同理得到FC＝FB，
∴△PEF的周长＝PE+EF+PF＝PE+EC+FC+PF
＝PE+EA+FB+PF
＝PA+PB
＝10+10
＝20（cm）．
故选：C．
5．如图，PA，PB是⊙O的切线，A，B是切点，若∠P＝80°，则∠ABO的度数是（ ）
A．40°B．45°C．50°D．55°
【答案】A
【解答】解：∵PA，PB是⊙O的切线，A，B是切点，
∴∠PBO＝∠PAO＝90°，
∵∠P＝80°，
∴∠BOA＝360°﹣∠PBO﹣∠PAO﹣∠P＝100°，
∵OA＝OB，
∴∠ABO＝∠BAO＝（180°﹣∠BOA）＝（180°﹣100°）＝40°，
故选：A．
6．如图，PA，PB为⊙O的两条切线，点A，B是切点，OP交⊙O于点C，交弦AB于点D．下列结论中错误的是（ ）
A．PA＝PBB．AD＝BDC．OP⊥ABD．∠PAB＝∠APB
【答案】D
【解答】解：由切线长定理可得：∠APO＝∠BPO，PA＝PB，从而AB⊥OP，AD＝BD．
因此A．B．C都正确．
无法得出∠PAB＝∠APB，可知：D是错误的．
综上可知：只有D是错误的．
故选：D．
7．如图，△ABC中，∠C＝90°，AC＝3，AB＝5，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则⊙O的半径为（ ）
A．1B．C．D．1.5
【答案】B
【解答】解：过点0作OE⊥AB于点E，OF⊥BC于点F．
∵AB、BC是⊙O的切线，
∴点E、F是切点，
∴OE、OF是⊙O的半径；
∴OE＝OF；
在△ABC中，∠C＝90°，AC＝3，AB＝5，
∴由勾股定理，得BC＝4；
又∵D是BC边的中点，
∴S△ABD＝S△ACD，
又∵S△ABD＝S△ABO+S△BOD，
∴AB•OE+BD•OF＝CD•AC，
即5×OE+2×OE＝2×3，
解得OE＝，
∴⊙O的半径是．
故选：B．
8．如图，AB是⊙O的直径，E为⊙O上一点，BD垂直平分OE交⊙O于点D，过点D的切线与BE的延长线交于点C．若，则AB的长为（ ）
A．4B．2C．D．
【答案】A
【解答】解：连接OD、AD，
∵DC是⊙O的切线，
∴OD⊥CD，
∵BD垂直平分OE交⊙O于点D，
∴∠ABD＝∠CBD＝∠ABC，OB＝BE，
∵∠ABD＝∠AOD，OB＝OE，
∴∠ABC＝∠AOD，△OBE是等边三角形，
∴OD∥BC，∠OBE＝60°，
∴BC⊥CD，∠ABD＝∠CBD＝∠ABC＝30°，
∵AB是⊙O的直径，
∴∠ADB＝90°＝∠DCB，
∴△ABD∽△DBC，
∴，
设AD＝x，则AB＝2x，BD＝，
∴，
∴x＝2，
∴AB＝2x＝4，
故选：A．
9．如图，在⊙O中，AB为直径，点M为AB延长线上的一点，MC与⊙O相切于点C，圆周上有一点D与点C分居直径AB两侧，且使得MC＝MD＝AC，连接AD．现有下列结论：
①MD与⊙O相切；②四边形ACMD是菱形；③AB＝MO；④∠ADM＝120°．
其中正确的结论有（ ）
A．4个B．3个C．2个D．1个
【答案】A
【解答】解：连接OC，OD，
∵OC＝OD，CM＝DM，OM＝OM，
∴△CMO≌△DMO（SSS），
∴∠ODM＝∠OCM，
∵MC与⊙O相切于点C，
∴∠OCM＝90°，
∴∠ODM＝90°，
∵OD是⊙O的直径，
∴MD与⊙O相切；故①正确；
∵△CMO≌△DMO，
∴∠COM＝∠DOM，
∴∠AOC＝∠AOD，
∵OA＝OA，
∴△AOC≌△AOD（SAS），
∴AC＝AD，
∴AC＝AD＝CM＝DM，
∴四边形ACMD是菱形，故②正确；
∵AC＝CM，
∴∠CAM＝∠CMA，
∵∠COM＝2∠CAM，
∴∠COM＝2∠CMO，
∴∠CMO＝30°，
∴OC＝OM，
∵OC＝AB，
∴AB＝OM，故③正确；
∵四边形ACMD是菱形，
∴∠DAM＝∠DMA＝∠AMC＝∠CAM＝30°，
∴∠ADM＝120°，故④正确；
故选：A．
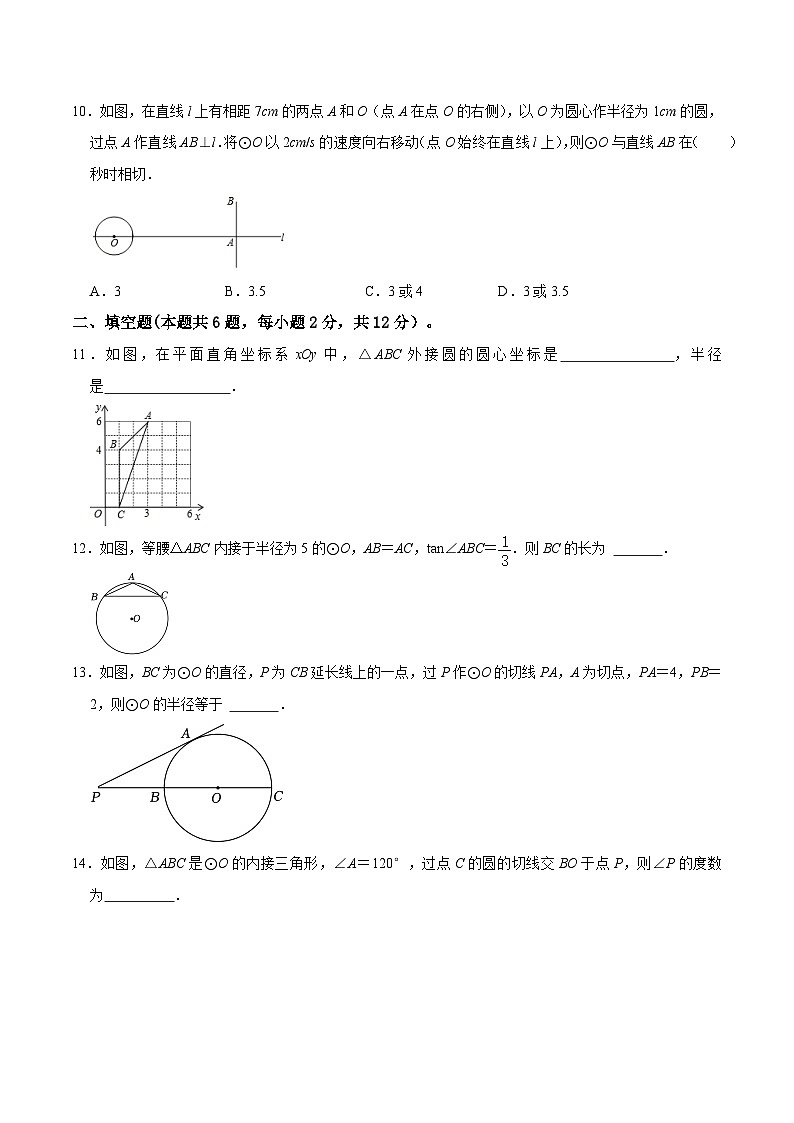
10．如图，在直线l上有相距7cm的两点A和O（点A在点O的右侧），以O为圆心作半径为1cm的圆，过点A作直线AB⊥l．将⊙O以2cm/s的速度向右移动（点O始终在直线l上），则⊙O与直线AB在（ ）秒时相切．
A．3B．3.5C．3或4D．3或3.5
【答案】C
【解答】解：当点O到AB的距离为1cm时，⊙O与AB相切，
∵开始时O点到AB的距离为7，
∴当圆向右移动7﹣1或7+1时，点O到AB的距离为1cm，此时⊙O与AB相切，
∴t＝＝3（s）或t＝＝4（s），
即⊙O与直线AB在3秒或4秒时相切．
故选：C．
二、填空题(本题共6题，每小题2分，共12分）。
11．如图，在平面直角坐标系xOy中，△ABC外接圆的圆心坐标是 （5，2） ，半径是 2 ．
【答案】见试题解答内容
【解答】解：∵△ABC外接圆的圆心到三角形三个顶点的距离相等，
又∵到B，C两点距离相等的点在BC的垂直平分线上，
∴三角形的外心位置基本确定，只有（5，2）点到三角形三个顶点距离相等，
∴（5，2）点是三角形的外接圆圆心．
利用勾股定理可得半径为：2．
故答案为：（5，2），2．
12．如图，等腰△ABC内接于半径为5的⊙O，AB＝AC，tan∠ABC＝．则BC的长为 6 ．
【答案】6．
【解答】解：连接OA，交BC于E，连接OB，
∵AB＝AC，
∴＝，
∵OA是⊙O的半径，
∴OA⊥BC，
∴BE＝EC，
∵tan∠ABC＝，
∴＝，
设AE＝x，则BE＝3x，OE＝5﹣x，
在Rt△OEB中，OB2＝OE2+BE2，即52＝（5﹣x）2+（3x）2，
解得：x1＝1，x2＝0（舍去），
∴BE＝3x＝3，
∴BC＝2BE＝6．
13．如图，BC为⊙O的直径，P为CB延长线上的一点，过P作⊙O的切线PA，A为切点，PA＝4，PB＝2，则⊙O的半径等于 3 ．
【答案】3．
【解答】解：连接OA，
∵PA是⊙O的切线，
∴∠PAO＝90°，∵PA＝4，PB＝2，
在Rt△PAO中，PO2＝PA2+AO2，
即（BO+2）2＝42+AO2，
∴（AO+2）2＝42+AO2，
解得AO＝3，
故答案为：3．
14．如图，△ABC是⊙O的内接三角形，∠A＝120°，过点C的圆的切线交BO于点P，则∠P的度数为 30° ．
【答案】见试题解答内容
【解答】解：如图所示：连接OC、CD，
∵PC是⊙O的切线，
∴PC⊥OC，
∴∠OCP＝90°，
∵∠A＝120°，
∴∠ODC＝180°﹣∠A＝60°，
∵OC＝OD，
∴∠OCD＝∠ODC＝60°，
∴∠DOC＝180°﹣2×60°＝60°，
∴∠P＝90°﹣∠DOC＝30°；
故答案为：30°．
15．如图，在⊙O中，直径AB与弦CD交于点E．＝2，连接AD，过点B的切线与AD的延长线交于点F．若∠AFB＝68°，则∠DEB＝ 66 °．
【答案】66．
【解答】解：如图，连接OC，OD，
∵BF是⊙O的切线，AB是⊙O的直径，
∴OB⊥BF，
∴∠ABF＝90°，
∵∠AFB＝68°，
∴∠BAF＝90°﹣∠AFB＝22°，
∴∠BOD＝2∠BAF＝44°，
∵，
∴∠COA＝2∠BOD＝88°，
∴∠CDA＝，
∵∠DEB是△AED的一个外角，
∴∠DEB＝∠BAF+∠CDA＝66°，
故答案为：66．
16．如图，半圆的圆心与坐标原点重合，半圆的半径1，直线l的解析式为y＝x+t．若直线l与半圆只有一个交点，则t的取值范围是 t＝或﹣1≤t＜1 ．
【答案】见试题解答内容
【解答】解：若直线与半圆只有一个交点，则有两种情况：直线和半圆相切于点C或从直线过点A开始到直线过点B结束（不包括直线过点A）．
直线y＝x+t与x轴所形成的锐角是45°．
当直线和半圆相切于点C时，则OC垂直于直线，∠COD＝45°．
又OC＝1，则CD＝OD＝，即点C（﹣，），
把点C的坐标代入直线解析式，得
t＝y﹣x＝，
当直线过点A时，把点A（﹣1，0）代入直线解析式，得t＝y﹣x＝1．
当直线过点B时，把点B（1，0）代入直线解析式，得t＝y﹣x＝﹣1．
即当t＝或﹣1≤t＜1时，直线和圆只有一个公共点；
故答案为t＝或﹣1≤t＜1．
三、解答题（本题共7题，共58分）。
17．如图，以△ABC的边AB为直径作⊙O，交边AC于点D，BC为⊙O的切线，弦DE⊥AB于点F，连结BE．
（1）求证：∠ABE＝∠C．
（2）若点F为OB中点，且OF＝1，求线段ED的长．
【答案】（1）见解答；
（2）2．
【解答】（1）证明：AB为直径，BC为⊙O的切线，
∴∠ABC＝90°，
∴∠A+∠C＝90°，
∵DE⊥AB，
∴∠BFE＝90°，
∴∠E+∠ABE＝90°，
∵∠E＝∠A，
∴∠ABE＝∠C．
（2）解：连接OE，
∵点F为OB中点，
∴OF＝OB＝OE，
∴∠OEF＝30°，
∵OF＝1，
∴OE＝2，EF＝，
∵弦DE⊥AB于点F，AB为直径，
∴DE＝2EF＝2．
18．如图，Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O，点D为⊙O上一点，且CD＝CB，连接DO并延长交CB的延长线于点E．
（1）判断直线CD与⊙O的位置关系，并证明；
（2）若BE＝8，DE＝16，求⊙O的半径．
【答案】（1）见解析；
（2）6．
【解答】解：（1）相切，
证明：如图，连接OC，
在△OCB与△OCD中，
，
∴△OCB≌△OCD（SSS），
∴∠ODC＝∠OBC＝90°，
∴OD⊥DC，
又∵OD为⊙O的半径，
∴DC是⊙O的切线；
（2）设⊙O的半径为r，
在Rt△OBE中，∵OE2＝EB2+OB2，
∴（16﹣r）2＝r2+82，
∴r＝6，
∴⊙O的半径为6．
19．如图，在Rt△AOB中，∠AOB＝90°，以点O为圆心，OA为半径的圆交AB于点C，点D在边OB上，且CD＝BD．
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）已知tan∠ODC＝，AB＝40，求⊙O的半径．
【答案】（1）直线CD与⊙O相切，理由见解析过程；
（2）24．
【解答】解：（1）直线CD与⊙O相切，
理由如下：如图，连接OC，
∵OA＝OC，CD＝BD，
∴∠A＝∠ACO，∠B＝∠DCB，
∵∠AOB＝90°，
∴∠A+∠B＝90°，
∴∠ACO+∠DCB＝90°，
∴∠OCD＝90°，
∴OC⊥CD，
又∵OC为半径，
∴CD是⊙O的切线，
∴直线CD与⊙O相切；
（2）∵tan∠ODC＝＝，
∴设CD＝7x＝DB，OC＝24x＝OA，
∵∠OCD＝90°，
∴OD＝＝＝25x，
∴OB＝32x，
∵∠AOB＝90°，
∴AB2＝AO2+OB2，
∴1600＝576x2+1024x2，
∴x＝1，
∴OA＝OC＝24，
∴⊙O的半径为24．
20．如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝6，DE＝5，求⊙O的直径．
【答案】（1）直线DE与⊙O相切，理由见解析；
（2）．
【解答】解：（1）直线DE与⊙O相切，
理由：连接DO，如图，
∵∠BDC＝90°，E为BC的中点，
∴DE＝CE＝BE，
∴∠EDC＝∠ECD，
又∵OD＝OC，
∴∠ODC＝∠OCD，
而∠OCD+∠DCE＝∠ACB＝90°，
∴∠EDC+∠ODC＝90°，即∠EDO＝90°，
∴DE⊥OD，
∵OD是⊙O的半径，
∴DE与⊙O相切；
（2）由（1）得，∠CDB＝90°，
∵CE＝EB，
∴DE＝BC，
∴BC＝10，
∴BD＝＝＝8，
∵∠BCA＝∠BDC＝90°，∠B＝∠B，
∴△BCA∽△BDC，
∴＝，
∴，
∴，
∴⊙O直径的长为．
21．如图，在△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC、AB于点E．F．
（1）试判断直线BC与⊙O的位置关系，并说明理由；
（2）若BD＝2，BF＝2，求⊙O的半径．
【答案】见试题解答内容
【解答】解：（1）线BC与⊙O的位置关系是相切，
理由是：连接OD，
∵OA＝OD，
∴∠OAD＝∠ODA，
∵AD平分∠CAB，
∴∠OAD＝∠CAD，
∴∠ODA＝∠CAD，
∴OD∥AC，
∵∠C＝90°，
∴∠ODB＝90°，即OD⊥BC，
∵OD为半径，
∴线BC与⊙O的位置关系是相切；
（2）设⊙O的半径为R，
则OD＝OF＝R，
在Rt△BDO中，由勾股定理得：OB2＝BD2+OD2，
即（R+2）2＝（2）2+R2，
解得：R＝4，
即⊙O的半径是4．
22．如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE＝，求⊙O的直径．
【答案】见试题解答内容
【解答】（1）证明：连接DO，如图，
∵直径所对圆周角，
∴∠ADC＝90°，
∴∠BDC＝90°，E为BC的中点，
∴DE＝CE＝BE，
∴∠EDC＝∠ECD，
又∵OD＝OC，
∴∠ODC＝∠OCD，
而∠OCD+∠DCE＝∠ACB＝90°，
∴∠EDC+∠ODC＝90°，即∠EDO＝90°，
∴DE⊥OD且OD为半径，
∴DE与⊙O相切；
（2）由（1）得，∠CDB＝90°，
∵CE＝EB，
∴DE＝BC，
∴BC＝5，
∴BD＝＝＝4，
∵∠BCA＝∠BDC＝90°，∠B＝∠B，
∴△BCA∽△BDC，
∴＝，
∴＝，
∴AC＝，
∴⊙O直径的长为．
23．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）如果AB＝5，BC＝6，求DE的长．
【答案】见试题解答内容
【解答】解：（1）相切，理由如下：
连接AD，OD，
∵AB为⊙O的直径，
∴∠ADB＝90°．
∴AD⊥BC．
∵AB＝AC，
∴CD＝BD＝BC．
∵OA＝OB，
∴OD∥AC．
∴∠ODE＝∠CED．
∵DE⊥AC，