专题28轴对称、平移、旋转过关检测-备战2024年中考数学一轮复习考点

这是一份专题28轴对称、平移、旋转过关检测-备战2024年中考数学一轮复习考点，文件包含专题28轴对称平移旋转过关检测教师版docx、专题28轴对称平移旋转过关检测考试版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。
一、选择题（本题共10小题，每小题3分，共30分）。
1．下列图形中，对称轴最多的图形是（ ）
A．B．
C．D．
【答案】A
【解答】解：A．该图有无数条对称轴；
B．该图有一条对称轴；
C．该图有两条对称轴；
D．该图有三条对称轴．
所以对称轴最多的图形是选项A．
故选：A．
2．如图，将△ABC沿直线DE折叠，使点C与点A重合，已知AB＝7，BC＝6，则△BCD的周长为（ ）
A．12B．13C．19D．20
【答案】B
【解答】解：由折叠可知，AD＝CD，
∵AB＝7，BC＝6，
∴△BCD的周长＝BC+BD+CD＝BC+BD+AD＝BC+AB＝7+6＝13．
故选：B．
3．在平面直角坐标系中，点（3，2）关于x轴对称的点是（ ）
A．（﹣3，2）B．（3，﹣2）C．（﹣3，﹣2）D．（﹣2，3）
【答案】B
【解答】解在平面直角坐标系中，点（3，2）关于x轴对称的点是（3，﹣2）．
故选：B．
4．在平面直角坐标系中，将点A（﹣3，﹣2）向右平移5个单位长度得到的点坐标为（ ）
A．（2，2）B．（﹣2，2）C．（﹣2，﹣2）D．（2，﹣2）
【答案】D
【解答】解：将点A（﹣3，﹣2）向右平移5个单位长度得到的点坐标为（﹣3+5，﹣2），即（2，﹣2），
故选：D．
5．“方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥．如图，将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′，形成一个“方胜”图案，则重叠部分的小正方形边长为（ ）
A．1cmB．2cmC．D．
【答案】C
【解答】解：∵四边形ABCD是正方形，
∵AB＝AD＝2cm，∠A＝90°，
∴BD＝AB＝2（cm），
由平移变换的性质可知BB′＝1cm，
∴DB′＝BD﹣BB﹣1）cm，
∴小正方形的边长＝DB′＝×（2﹣1）＝（2﹣）cm，
故选：C．
6．如图，把三角形ABC沿BC方向平移1个单位长度得到三角形DEF，若四边形ABFD的周长为10，则三角形ABC的周长为（ ）
A．8B．10C．12D．14
【答案】A
【解答】解：∵把三角形ABC沿BC方向平移1个单位长度得到三角形DEF，
∴AD＝BE＝1，△ABC≌△DEF，
∵四边形ABFD的周长为10，
∴AD+BF+AB+DF＝10，
∵BF＝BE+EF＝1+EF，
∴1+1+EF+AB+DF＝10，即EF+AB+DF＝8，
又∵DF＝AC，EF＝BC，
∴AB+AC+BC＝8，
∴三角形ABC的周长为：8．
故选：A．
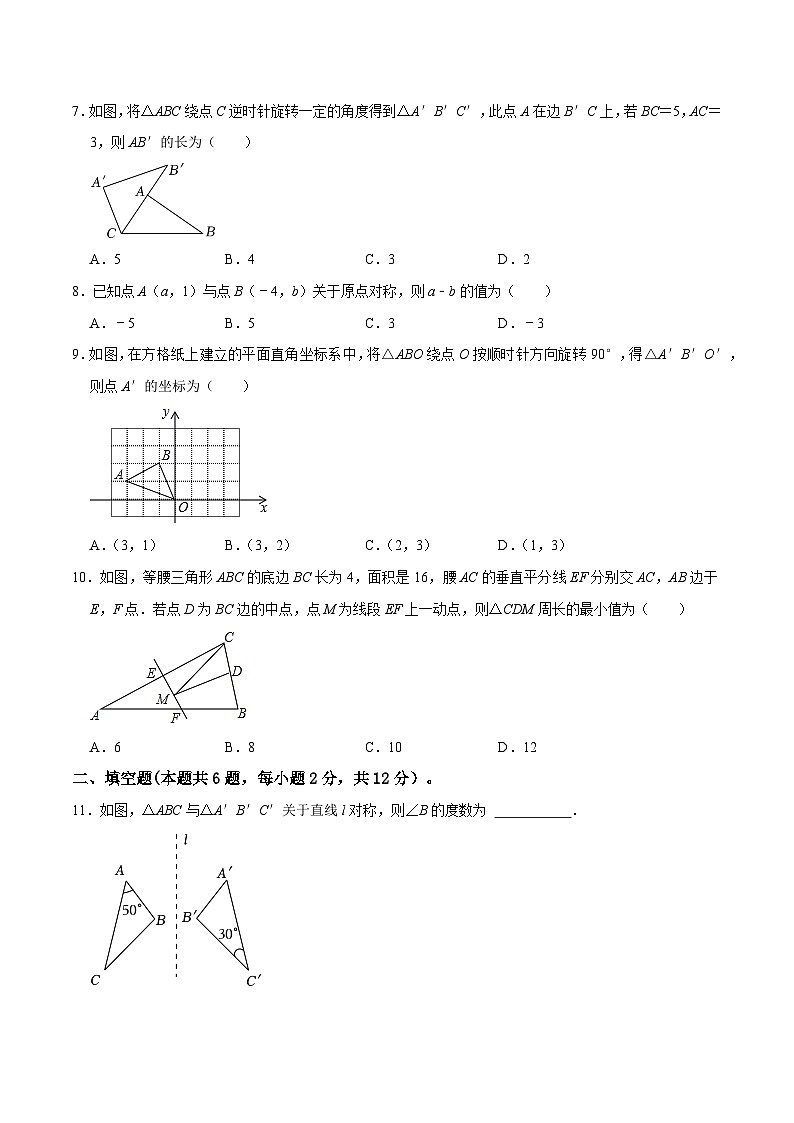
7．如图，将△ABC绕点C逆时针旋转一定的角度得到△A′B′C′，此点A在边B′C上，若BC＝5，AC＝3，则AB′的长为（ ）
A．5B．4C．3D．2
【答案】D
【解答】解：∵△ABC绕点C逆时针旋转一定的角度得到△A′B′C′，点A在边B′C上，
∴CB′＝CB＝5，
∴AB′＝CB′﹣CA＝5﹣3＝2．
故选：D．
8．已知点A（a，1）与点B（﹣4，b）关于原点对称，则a﹣b的值为（ ）
A．﹣5B．5C．3D．﹣3
【答案】B
【解答】解：∵点A（a，1）与点B（﹣4，b）关于原点对称，
∴a＝4，b＝﹣1．
∴a﹣b＝4﹣（﹣1）＝5．
故选：B．
9．如图，在方格纸上建立的平面直角坐标系中，将△ABO绕点O按顺时针方向旋转90°，得△A′B′O′，则点A′的坐标为（ ）
A．（3，1）B．（3，2）C．（2，3）D．（1，3）
【答案】D
【解答】解：如图，点A′的坐标为（1，3）．
故选D．
10．如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（ ）
A．6B．8C．10D．12
【答案】C
【解答】解：连接AD，
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC＝BC•AD＝×4×AD＝16，解得AD＝8，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴AD的长为CM+MD的最小值，
∴△CDM的周长最短＝CM+MD+CD＝AD+BC＝8+×4＝8+2＝10．
故选：C．
二、填空题(本题共6题，每小题2分，共12分）。
11．如图，△ABC与△A′B′C′关于直线l对称，则∠B的度数为 100° ．
【答案】100°．
【解答】解：∵△ABC与△A′B′C′关于直线l对称，
∴∠C＝∠C′＝30°；
∴∠B＝180°﹣50°﹣30°＝100°．
故答案为：100°．
12．如图，已知矩形ABCD，AB＝18cm，AD＝10cm，在其矩形内部有三个小矩形，则这三个小矩形的周长之和为 56 cm．
【答案】56．
【解答】解：由平移的性质以及矩形周长的定义可知，
这三个小矩形的周长之和为2AD+2AB＝56（cm），
故答案为：56．
13．如图，有一块长为44m、宽为24m的长方形草坪，其中有三条直道将草坪分为六块，则分成的六块草坪的总面积是 880 m2．
【答案】见试题解答内容
【解答】解：S＝44×24﹣2×24×2﹣2×44+2×2×2＝880（m2）．
故答案为：880．
14．如图，点A的坐标为（0，1），点B是x轴正半轴上的一点，将线段AB绕点A按逆时针方向旋转90°得到线段AC．若点C的坐标为（m，5），则B点的坐标为 （4，0） ．
【答案】（4，0）．
【解答】解：过C作CD⊥y轴于点D，如图：
∵∠BAC＝90°，
∴∠BAO+∠CAD＝90°，
∵∠ABO+∠BAO＝90°，
∴∠CAD＝∠ABO，
∵∠AOB＝∠CDA＝90°，AB＝AC，
∴△AOB≌△CDA（AAS），
∵OA＝CD，OB＝AD，
∵点A的坐标为（0，1），点C的坐标为（m，5），
∴OA＝1，AD＝5﹣1＝4，
∴OB＝4，
∴B（4，0），
故答案为：（4，0）．
15．在△ABC中，AB＝AC，∠A＝36°，将△ABC 绕点B逆时针旋转得到△DBE，旋转角为α（α＜90°），点C的对应点E落在△ABC边上时，旋转角α的度数为 36°或72° ．
【答案】36°或72°．
【解答】解：∵AB＝AC，∠A＝36°，
∴∠ABC＝∠C＝（180°﹣∠A）＝72°，
分两种情况：
当点C的对应点E落在边AC上时，如图：
由旋转得：BE＝BC，
∴∠C＝∠BEC＝72°，
∴∠EBC＝180°﹣∠C﹣∠BEC＝36°，
∴旋转角α的度数为36°；
当点C的对应点E落在边AB上时，如图：
∵∠ABC＝72°，
∴旋转角α的度数为72°；
综上所述：旋转角α的度数为36°或72°，
故答案为：36°或72°．
16．如图，等腰Rt△ABC中，D是AC上一动点，连接BD．将△BCD绕点B逆时针旋转90°得到△BAE，连接ED．若BC＝5，则△AED周长最小值是 5+5 ．
【答案】5+5．
【解答】解：∵将△BCD绕点B逆时针旋转90°得到△BAE，
∴AE＝CD，BE＝BD，∠DBE＝90°，
∴AE+AD＝AD+CD＝AC，△DBE是等腰直角三角形，
∴DE＝BD，
∴当BD取最小值时，DE的值最小，则△AED周长的值最小，
当BD⊥AC时，BD的值最小，
∵△ABC是等腰直角三角形，BC＝5，
∴AC＝BC＝5，
∴BD＝AC＝，
∴DE＝5，
∴△AED周长最小值是AC+DE＝5+5，
故答案为：5+5．
三、解答题（本题共7题，共58分）。
17．（8分）已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．（正方形网格中，每个小正方形的边长是1个单位长度）
（1）画出△ABC向下平移4个单位，再向左平移1个单位得到的△A1B1C1，并直接写出C1点的坐标；
（2）画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2，并直接写出C2点的坐标；
（3）请求出（2）中△ABC旋转过程中所扫过的面积为 ．
【答案】见试题解答内容
【解答】解：（1）如图1，C1（1，﹣2）；
（2）如图2，C2（﹣1，1）；
（3）∵AB＝＝，AC＝，BC＝，
∴AC2+BC2＝AB2，
∴△ABC是等腰直角三角形，
∴S△ABC＝＝，
∴△ABC旋转过程中所扫过的面积＝+S△ABC＝．
故答案为：．
18．（8分）有一块直角三角形纸片，两直角边分别为：AC＝6cm，BC＝8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD的长．
【答案】见试题解答内容
【解答】解：∵△ACD与△AED关于AD成轴对称，
∴AC＝AE＝6cm，CD＝DE，∠ACD＝∠AED＝∠DEB＝90°，
在Rt△ABC中，AB2＝AC2+BC2＝62+82＝102，
∴AB＝10，
∴BE＝AB﹣AE＝10﹣6＝4，
设CD＝DE＝xcm，则DB＝BC﹣CD＝8﹣x，
在Rt△DEB中，由勾股定理，得x2+42＝（8﹣x）2，
解得x＝3，即CD＝3cm．
19．（8分）如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．线段CD绕点C顺时针旋转60°得到线段CE，连接AE．求证：AE＝BD．
【答案】见解析．
【解答】证明：由旋转可知∠DCE＝60°，CD＝CE，
∵△ABC是等边三角形，
∴∠ACB＝60°，AC＝BC，
∴∠ACB+∠ACD＝∠DCE+∠ACD，
即∠BCD＝∠ACE，
在△BCD和△ACE中，
∴△BCD≌△ACE（SAS），
∴AE＝BD．
20．（8分）如图是4×4正方形网格，其中已有3个小方格涂成了黑色．现在要从其余13个白色小方格中选出一个涂成黑色，使整个涂成黑色的图形成为轴对称图形．在下面每个网格中画出一种符合要求的图形（画出三种即可）．
【答案】见试题解答内容
【解答】解：如图所示．
．
21．（8分）△ABC和△DEC是等腰直角三角形，∠ACB＝∠DCE＝90°，AC＝BC，CD＝CE．
【观察猜想】当△ABC和△DEC按如图1所示的位置摆放，连接BD、AE，延长BD交AE于点F，猜想线段BD和AE有怎样的数量关系和位置关系．
【探究证明】如图2，将△DCE绕着点C顺时针旋转一定角度α（0°＜α＜90°），线段BD和线段AE的数量关系和位置关系是否仍然成立？如果成立，请证明；如果不成立，请说明理由．
【拓展应用】如图3，在△ACD中，∠ADC＝45°，CD＝，AD＝4，将AC绕着点C逆时针旋转90°至BC，连接BD，求BD的长．
【答案】【观察猜想】AE⊥BD，AE＝BD；
【探究证明】线段BD和线段AE的数量关系和位置关系仍然成立，证明见解答过程；
【拓展应用】BD＝2．
【解答】解：【观察猜想】AE⊥BD，AE＝BD，
证明：在△ACE和△BCD中，
，
∴△ACE≌△BCD（SAS），
∴AE＝BD，∠CAE＝∠CBD，
∵∠ACB＝∠DCE＝90°，
∴∠CAE+∠AEC＝90°，
∵∠CAE＝∠CBD，∠AEC＝∠BEF，
∴∠DBC+∠BEF＝90°，
∴∠BFE＝180°﹣90°＝90°，
∴AE⊥BD；
【探究证明】线段BD和线段AE的数量关系和位置关系仍然成立，
证明：∵∠ACB＝∠DCE＝90°，
∴∠ACB+∠ACD＝∠DCE+∠ACD，
即∠ACE＝∠BCD，
在△ACE和△BCD中，
，
∴△ACE≌△BCD（SAS），
∴AE＝BD，∠CAE＝∠CBD，
∵∠ACB＝90°，
∴∠CBD+∠CGB＝90°，
∵∠CAE＝∠CBD，∠AGF＝∠CGB，
∴∠CAE+∠AGF＝90°，
∴∠BFA＝180°﹣90°＝90°，
∴AE⊥BD；
【拓展应用】如图，在CD的左侧以C为直角顶点作等腰直角△CDE，连接AE，
∴∠DCE＝90°，CE＝CD＝，∠CDE＝45°，
∴DE＝＝2，
∵∠ADC＝45°，
∴∠ADE＝∠ADC+∠CDE＝45°+45°＝90°，
∴AE＝＝＝2，
∵将AC绕着点C逆时针旋转90°至BC，
∴∠ACB＝90°，AC＝BC，
由【探究证明】知BD＝AE，
∴BD＝2．
22．（8分）如图，四边形ABCD是矩形，E、F分别是线段AD、BC上的点，点O是EF与BD的交点．若将△BED沿直线BD折叠，则点E与点F重合．
（1）求证：四边形BEDF是菱形；
（2）若ED＝2AE，AB•AD＝3，求EF•BD的值．
【答案】（1）详见解答过程；
（2）EF•BD＝4．
【解答】解：（1）证明：将△BED沿BD折叠，使E，F重合，
∴OE＝OF，EF⊥BD，
∵四边形ABCD是矩形，
∴∠C＝90°，AD∥BC，
∴∠ODE＝∠OBF，
在△OBF和△ODE中，
，
∴△OBF≌△ODE（AAS），
∴OB＝OD，
∵OE＝OF，
∴四边形BFDE是平行四边形，
∵EF⊥BD，
∴四边形BFDE是菱形．
（2）如图，∵AB•AD＝3，
∴S△ABD＝AB•AD＝，
∵ED＝2AE，
∴ED＝AD，
∴S△BDE：S△ABD＝2：3，
∴S△BDE＝，
∴菱形BEDF的面积＝EF•BD＝2S△BDE＝2，
∴EF•BD＝4．
23．（10分）综合与实践：
在综合与实践课上，老师让同学们以“矩形纸片的折叠”为主题开展数学活动．
在矩形ABCD中，E为AB边上一点，F为AD边上一点，连接CE、CF，分别将△BCE和△CDF沿CE、CF翻折，点D、B的对应点分别为点G、H，且C、H、G三点共线．
（1）如图1，若F为AD边的中点，AB＝BC＝6，点G与点H重合，则∠ECF＝ 45 °，BE＝ 2 ；
（2）如图2，若F为AD的中点，CG平分∠ECF，，BC＝2，求∠ECF的度数及BE的长．
（3）AB＝5，AD＝3，若F为AD的三等分点，请直接写出BE的长．
【答案】（1）45；2；
（2）45°；2﹣2；
（3）2或．
【解答】.解：（1）∵AB＝BC，四边形ABCD是矩形，
∴四边形ABCD是正方形，
∴AD＝AB＝6，∠BCD＝90°，
∵F为AD的中点，
∴DF＝AF＝3，
∵将△BCE和△CDF沿CE、CF翻折，点D、B的对应点分别为点G、H，
∴BE＝EG，DF＝FG＝3，
设BE＝x，则AE＝6﹣x，
∴EF＝3+x，
∵EF2＝AE2+AF2，
∴（3+x）2＝（6﹣x）2+32，
∴x＝2，
∴BE＝2．
∵将△BCE和△CDF沿CE、CF翻折，点D、B的对应点分别为点G、H，
∴∠BCE＝∠GCE，∠DCF＝∠GCF，
∵∠BCD＝90°，
∴∠ECF＝∠BCD＝°＝45°．
故答案为：45；2；
（2）如图2，延长CG，交AB于点M，
∵CG平分∠ECF，
∴∠2＝∠4．
由折叠的性质可知，∠1＝∠2，∠3＝∠4．
∴∠1＝∠2＝∠3＝∠4＝∠BCD＝22.5°，
∴∠ECF＝45°．
∵CD∥AB，∠EMH＝∠DCM＝45°，
∴△CBM和△EHM均为等腰直角三角形，
∴BM＝BC＝2，EM＝BE，
∴BE+EM＝2，
即BE+BE＝2，
解得BE＝2﹣2．
（3）2或．
分两种情况：①当AF＝2DF时，
如图3，过点E作EP∥GH，交FG的延长线于点P，连接EF，则四边形GHEP为矩形，GH＝EP，EH＝GP，
由折叠的性质可知，CD＝CG＝5，BC＝CH＝3，
∴HG＝CG﹣CH＝2，
∵AF＝2DF，
∴AF＝2，
∴AF＝EP，
在Rt△EFP和Rt△FEA中，
，
∴Rt△EFP≌Rt△FEA（HL），
∴AE＝FP，
设BE＝EH＝a，FP＝a+1，AE＝FP＝5﹣a，
∴a+1＝5﹣a，
解得a＝2，
∴BE＝2．
②当DF＝2AF时，
如图4，过点E作EP∥GH，交FG的延长线于点P，连接EF，则四边形GHEP为矩形，GH＝EP，EH