初中数学苏科版八年级下册11.1 反比例函数课后复习题

这是一份初中数学苏科版八年级下册11.1 反比例函数课后复习题，文件包含专题30反比例函数与一次函数结合原卷版docx、专题30反比例函数与一次函数结合解析版docx等2份试卷配套教学资源，其中试卷共45页， 欢迎下载使用。
1．（2022春·江苏苏州·八年级校考期末）我们定义：如果一个矩形周长和面积都是矩形的倍，那么我们就称矩形是矩形的完全倍体．
(1)若矩形为正方形，是否存在一个正方形是正方形的完全倍体？______（填“存在”或“不存在”）．
【深入探究】
长为，宽为的矩形是否存在完全倍体？
小鸣和小棋分别有以下思路：
【小鸣方程流】设新矩形长和宽为、，则依题意，
联立得，再探究根的情况；
【小棋函数流】如图，也可用反比例函数：与一次函数：来研究，作出图象，有交点，意味着存在完全倍体．
(2)那么长为．宽为的矩形是否存在完全倍体？请利用上述其中一种思路说明原因．
(3)如果长为，宽为的矩形存在完全倍体，请直接写出的取值范围：______．
【答案】(1)不存在
(2)长为．宽为的矩形不存在完全倍体，利用思路说明原因见解析
(3)
【分析】（1）根据“完全N倍体”的定义及题干示例解答即可；
（2）运用新定义“完全N倍体”及【小鸣方程流】和【小棋函数流】的方法分别解答即可；
（3）设所求矩形的长为x,则所求矩形的宽为：k（3+2）-x,即5k-x,根据新定义“完全N倍体”可得： -5kx+6k=0，再运用根的判别式即可求得答案．
（1）
不存在．
因为两个正方形是相似图形，当它们的周长比为时，则面积比必定是，所以不存在．
故答案为：不存在；
[深入探究]
长为，宽为的矩形存在完全倍体矩形，
∵矩形长为，宽为，
矩形的周长为，面积为，
[小鸣方程流]设新矩形长和宽为、，则依题意，
联立，
整理得，
解得：，，
新矩形的长为，宽为时，周长为，面积为，
长为，宽为的矩形存在完全倍体矩形．
[小棋函数流]如图，设新矩形长和宽为、，则依题意，
即，，
利用反比例函数：与一次函数：来研究，作出图象，有交点，意味着存在完全倍体．
（2）
长为，宽为的矩形的周长为，面积为，
[小鸣方程流】设新矩形长和宽为、，则依题意，，
联立得，
整理得：，
，
此方程没有实数根，即长为宽为的矩形不存在完全倍体；
[小棋函数流]如图，设新矩形长和宽为、，则依题意，
即，，
利用反比例函数：与一次函数：来研究，作出图象，无交点，意味着不存在完全倍体．
（3）
设所求矩形的长为，则所求矩形的宽为：，即，
由题意得：，
整理得：，
，
一定存在另一个矩形的周长和面积分别是已知矩形周长和面积倍，
，即：，
令，为开口向上的抛物线，
则由，可得：，
解得：，，
当时，或，
不符合题意，
的取值范围为：；
故答案为：．
【点睛】本题考查了一元二次方程的应用，根的判别式．需要认真阅读理解新定义“矩形A是矩形B的完全N倍体”，根据题干过程模仿解题．第（3）题应用一元二次方程根的判别式求k的范围．
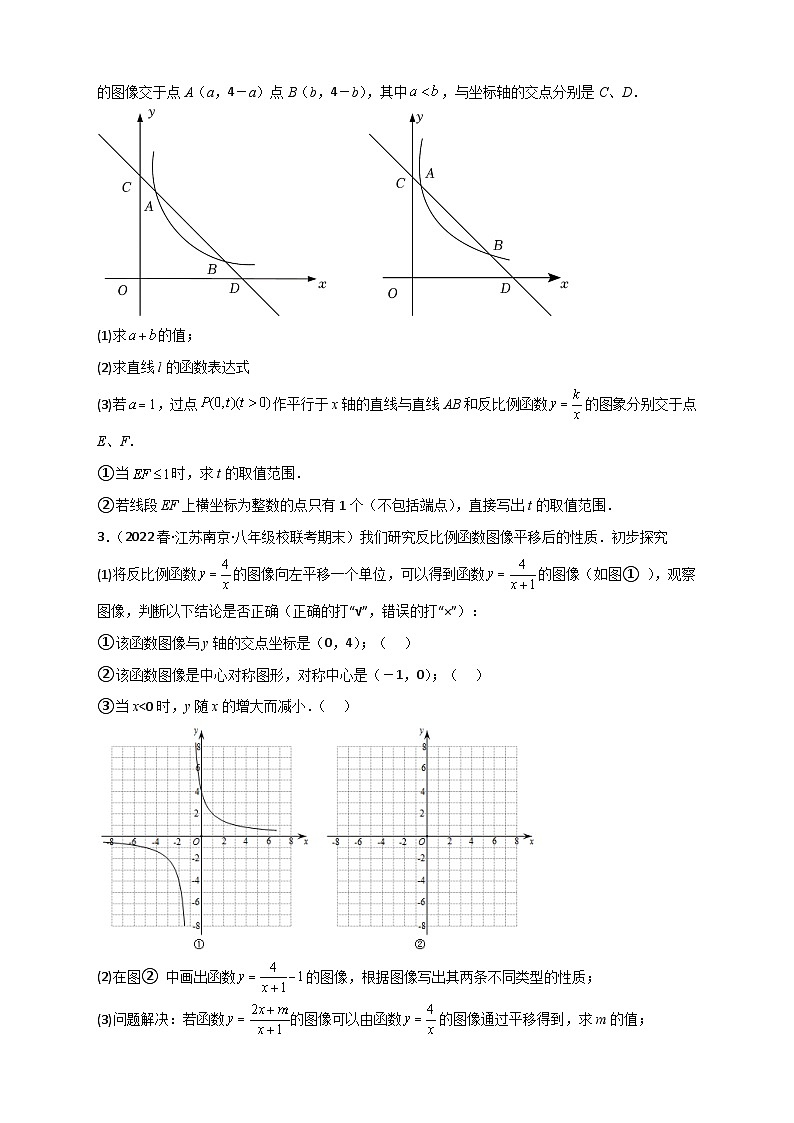
2．（2022春·江苏泰州·八年级统考期末）如图，在平面直角坐标系中，直线l与反比例函数的图像交于点A（a，4－a）点B（b，4－b），其中，与坐标轴的交点分别是C、D．
(1)求的值；
(2)求直线l的函数表达式
(3)若，过点作平行于x轴的直线与直线AB和反比例函数的图象分别交于点E、F．
①当时，求t的取值范围．
②若线段EF上横坐标为整数的点只有1个（不包括端点），直接写出t的取值范围．
【答案】(1)
(2)
(3)①；②或
【分析】（1）把、点坐标代入反比例函数解析式，得、的关系，再通过因式分解，解方程可得的值；
（2）用待定系数法求解即可；
（3）①当时，可得反比例函数的解析式为：，；根据题意可知，，，，再根据题意，对进行讨论即可；②根据题意，作直线，，，，分别与反比例函数交于点，，，，结合图形可直接得出结论．
（1）
解：直线与反比例函数的图象交于点，点，
，
，
，
，
，
；
（2）
设直线的解析式为，把，点代入得，
，
解得，，
直线的解析式为；
（3）
①当时，，
，
反比例函数的解析式为：，
令，解得或，
．
过点，作平行于轴的直线与直线和反比例函数的图象分别交于点、，
，，，
当时，点在点的左侧，
，整理得，方程恒成立；
当或时，，重合，则；
当或时，，
整理得，，解得，
或，
综上，当时，的取值范围为：．
②如图，作直线，，，，分别与反比例函数交于点，，，，
，，，．
由图可知，若线段上横坐标为整数的点只有1个（不包括端点），则的取值范围为：或．
【点睛】本题主要考查反比例函数的综合题，涉及待定系数法求函数解析式，反比例函数上的点的特征，数形结合思想，方程思想等相关内容，利用数形结合思想，画出给出图象是解题关键．
3．（2022春·江苏南京·八年级校联考期末）我们研究反比例函数图像平移后的性质．初步探究
(1)将反比例函数的图像向左平移一个单位，可以得到函数的图像（如图① ），观察图像，判断以下结论是否正确（正确的打“√”，错误的打“×”）：
①该函数图像与y轴的交点坐标是（0，4）；（ ）
②该函数图像是中心对称图形，对称中心是（－1，0）；（ ）
③当x0时，对于任意正数k，方程均无解，直接写出a，b，k满足的数量关系．
【答案】(1)①对；②对；③错
(2)图见解析，性质见解析
(3)m＝6
(4)a－b＋k＝0
【分析】（1）通过观察图象，分析图象性质即可判断是否正确；
（2）利用5点作图法在坐标轴上描点即可作图；
（3）通过化简运算，结合题意，即可求m的值；
（3）由反比例函数无解时的性质，即可写出a，b，k满足的数量关系．
【详解】（1）观察图可得，该函数图象与y轴的交点坐标是（0，4），故①√；
该函数是反比例函数，是中心对称图形，对称中心易知是（-1，0），故②√；
当-1＜x＜0时，y随x的增大而减小，当x＜-1，y随x的增大而减小，但并不连续区间，故不为单调递减，③错误；
故答案为：①√；②√；③×；
（2）函数图像如图所示．
两条不同类型的性质是：
例如：
① 当x－1时，y随x的增大而减小；
② 无论x取何值，图数值不等于－1；
③ 该图数图像与y轴的交点坐标是（0，3）；
④该图数图像与x轴的交点坐标是（3，0）；
⑤该函数图像是中心对称图形，对称中心是（－1，－1）；
⑥ 该函数图像是轴对称图形，对称轴是直线y＝x和y＝－x－2．
（3）；
根据题意，得m－2＝4，
解得m＝6．
（4），
，
，
∵对于任意k，方程均无解，当x=-1时分式无意义，
∴a+k-b=0
【点睛】本题考查了反比例函数的图象与性质；正确作图、理解题意、综合分析是本题解题的关键．
4．（2022春·江苏泰州·八年级统考期末）如图所示，直线y=ax+b （a0）的图像与x轴交于点A，与y轴交于点B， 与反比例函数y=（x