




专题03 二次函数与一元二次方程重难点题型专训-2023-2024学年九年级数学上册重难点高分突破(浙教版)
展开题型一 求抛物线与x、y轴的交点坐标
题型二 由二次函数解一元二次方程
题型三 由二次函数的图象求不等式的解集
题型四 抛物线交点问题的综合
题型五 根据二次函数图象确定相应方程根的情况
题型六 求x轴与抛物线的截线长
【知识梳理】
知识点:二次函数与一元二次方程
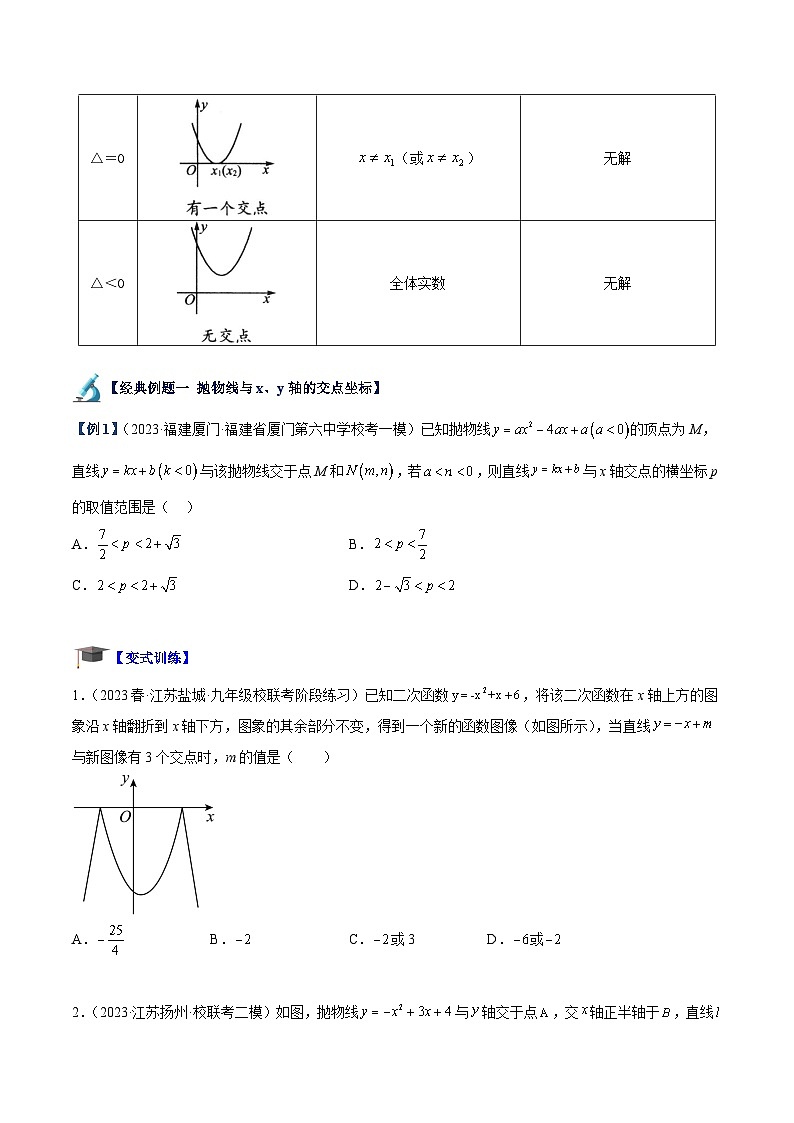
1.当二次函数的图象与x轴有两个交点时,,方程有两个不相等的实根。
2.当二次函数的图象与x轴有且只有一个交点时,,方程有两个相等的实根。
3.当二次函数的图象与x轴没有交点时,,方程没有实根。
二次函数的图象与轴的位置关系有三种情况:①没有公共点;②有一个公共点;③有两个公共点,这对应着一元二次方程的根的三种情况:
①有实数根,此时△<0;②有两个相等的实数根,此时△=0;③有两个不相等的实数根,此时△>0.
(2)解决函数图象过定点问题,一般方法是函数解析式中所含字母的项的和为0时,则函数值不受字母的影响,据此可求图象经过的定点坐标.
(3)抛物线中三角形面积的最值问题,一般先设出动点的坐标,然后用其表示相关线段的长度,再利用三角形的面积公式构造新的函数关系式来确定最值.在将点的坐标转化为线段的长度时,要注意符号的转换.
知识点:二次函数与不等式
【经典例题一 抛物线与x、y轴的交点坐标】
【例1】(2023·福建厦门·福建省厦门第六中学校考一模)已知抛物线的顶点为M,直线与该抛物线交于点M和,若,则直线与x轴交点的横坐标p的取值范围是( )
A.B.
C.D.
【变式训练】
1.(2023春·江苏盐城·九年级校联考阶段练习)已知二次函数,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图像(如图所示),当直线与新图像有3个交点时,m的值是( )
A.B.C.或3D.或
2.(2023·江苏扬州·校联考二模)如图,抛物线与轴交于点,交轴正半轴于,直线过,是抛物线第一象限内一点,过点作轴交直线于点,则的最大值为______.
3.(2023·新疆喀什·统考三模)如图,抛物线交x轴于、B两点,交y轴于,点P在抛物线上,横坐标设为m.
(1)求抛物线的解析式;
(2)当点P在x轴上方时,直接写出m的取值范围;
(3)若抛物线在点P右侧部分(含点P)的最高点的纵坐标为,求m的值.
【经典例题二 由二次函数解一元二次方程】
【例2】(2023秋·山东淄博·九年级校考期末)已知二次函数 (a,k,h均为常数)的图象与x轴的交点的横坐标分别为和5,则关于x的一元二次方程的两个实数根分别是( )
A.B.C.D.
【变式训练】
1.(2022秋·湖北武汉·九年级湖北省水果湖第一中学校考期中)抛物线的图象经过点,则关于x的一元二次方程的解是( )
A.B.C.D.
2.(2023·吉林长春·统考一模)在平面直角坐标系中,抛物线经过点.若关于的一元二次方程(为实数)在的范围内有实数根,则的取值范围为______.
3.(2023·湖北黄石·统考一模)阅读材料:
材料1.已知实数m、n满足,且,求的值.
解:由题意知m、n是方程的两个不相等的实数根,得,
∴
材料2.如图,函数的图像,是一条连续不断的抛物线,因为当时,;当时,.可知抛物线与x轴的一个交点的横坐标在0与1之间.
所以方程的一个根所在的范围是.
根据上述材料解决下面问题:
(1)已知实数m、n满足,,且,求的值.
(2)已知实数p、q满足,,,且,求的值.
(3)若关于x的一元二次方程的一个根大于2,另一个根小于2,求m的取值范围.
【经典例题三 由二次函数的图象求不等式的解集】
【例3】(2022·内蒙古呼和浩特·校考一模)已知关于的一元二次方程的一个根为,二次函数的图象的顶点坐标为,则关于的不等式的解为( )
A.或B.或C.D.
【变式训练】
1.(2023·山东东营·统考一模)如图,抛物线和直线都经过点,抛物线的对称轴为,那么下列说法正确的是( )
A.B.
C. D.是不等式的解
2.(2023·上海普陀·统考二模)抛物线开口向上,且过,下列结论中正确的是_________(填序号即可).
①若抛物线过,则;
②若,则不等式的解为;
③若,、为抛物线上两点,则时;
④若抛物线过,且,则抛物线的顶点一定在的下方.
3.(2023·广东深圳·深圳市福田区北环中学校考二模)请阅读下列解题过程:解一元二次不等式:.
解:设,解得:,,
则抛物线与轴的交点坐标为和.
画出二次函数的大致图象(如图所示).
由图象可知:当时函数图象位于轴下方,
此时,即.
所以一元二次不等式的解集为:.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的_________和_________(只填序号)
①转化思想;②分类讨论思想;③数形结合思想.
(2)用类似的方法解一元二次不等式:.
(3)某“数学兴趣小组”根据以上的经验,对函数的图象和性质进行了探究,探究过程如下,请补充完整:
①自变量的取值范围是___________;与的几组对应值如表,其中___________.
②如图,在直角坐标系中画出了函数的部分图象,用描点法将这个图象补画完整.
③结合函数图象,解决下列问题:
解不等式:
【经典例题四 抛物线交点问题的综合】
【例4】(2023·山东济南·统考二模)二次函数分别交x轴、y轴于P,Q两点,点C的坐标是(2,1).若在线段上存在A,B两点使得为等腰直角三角形,且,则b的取值范围是( )
A.或B.或C.D.
【变式训练】
1.(2022秋·河北沧州·九年级统考期末)已知抛物线(a,b,c为常数,)经过点,且对称轴为直线,有下列结论:①;②;③无论a,b,c取何值,抛物线一定经过.其正确结论有( )个
A.0B.1C.2D.3
2.(2023秋·北京海淀·九年级期末)已知抛物线().现给出以下结论:①该抛物线与y轴的交点坐标是;②当时,抛物线与直线没有交点;③若该抛物线的顶点在直线与坐标轴围成的三角形内(包括边界),则;④若抛物线与x轴有两个交点,则其中一定有一个交点在点与之间.其中正确的是______________.(写出所有正确结论的序号)
3.(2022秋·广东广州·九年级统考期末)在平面直角坐标系中,点都在抛物线上.
(1)当时,求的值;
(2)当时,求的取值范围;
(3)在(1)的条件下,设抛物线与轴正半轴交于点A,与轴交于点B. 将抛物线沿着轴向上平移个单位长度得到抛物线,若抛物线与轴交于C,D两点,与轴交于点E,且,. 求抛物线在的最高点的纵坐标.
【经典例题五 根据二次函数图象确定相应方程根的情况】
【例5】(2022秋·河南安阳·九年级统考期中)一元二次方程的两个根分别为和4,若二次函数与轴的交点为,,则对于,的范围描述正确的是( )
A.B.C.D.
【变式训练】
1.(2022秋·浙江杭州·九年级校考期中)已知,关于的一元二次方程的解为, ,则下列结论正确的是( )
A. B.C. D.
2.(2022秋·浙江丽水·九年级校联考期中)已知二次函数的图象上有两点和,则的值等于 _____.
3.(2022秋·浙江·九年级期中)宏志班“数学兴趣小组”对函数的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数,与的几组对应值列表如下:
其中,
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质:① ;② .
(4)关于的方程有4个实数根时,的取值范围是 .
【经典例题六 求x轴与抛物线的截线长】
【例6】(2023·广东梅州·统考一模)已知抛物线与一次函数交于两点,则线段的长度为( )
A.B.C.D.20
【变式训练】
1.(2022秋·浙江台州·九年级统考期末)已知二次函数,当 时,,则当 时,的取值范围为 ( )
A.B.C.D.不能确定
2.(2022春·全国·九年级专题练习)已知抛物线与x轴交于 A,B两点,则线段AB的长的最小值为______.
3.(2023·河南洛阳·统考一模)在平面直角坐标系中,已知抛物线.
(1)抛物线的顶点坐标为______(用含m的式子表示);
(2)已知抛物线与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
①若,求抛物线的解析式;
②若,请直接写出m的取值范围.
【重难点训练】
1.(2023·浙江杭州·杭州市十三中教育集团(总校)校考二模)函数的图象与x轴两个交点的横坐标分别为,,且,,当时,该函数的最小值m与b的关系式是( )
A.B.C.D.
2.(2023·浙江台州·台州市书生中学统考一模)抛物线交x轴于,A两点,将绕点A旋转得到抛物线,交x轴于另一点;将绕点旋转得到抛物线,交x轴于另一点;…,如此进行下去,形成如图所示的图像,则下列各点在图像上的是( )
A.B.C.D.
3.(2023春·浙江杭州·九年级翠苑中学校考阶段练习)在平面直角坐标系中,已知函数,,其中a,b是正实数,且,设,的图象与x轴交点个数分别是M,N,则( )
A.或或B.或
C.或D.或或
4.(2023·浙江绍兴·统考一模)已知点,,都在抛物线上,,下列选项正确的是( )
A.若,则B.若,则
C.若,则D.若,则
5.(2022秋·浙江金华·九年级校联考阶段练习)二次函数的部分图象如图所示,其对称轴为直线,且与x轴的一个交点坐标为,下列结论:①;②;③图象与x轴的另一个交点坐标为;④关于x的一元二次方程有两个相等的实数根;⑤.其中正确的结论个数是( )
A.2B.3C.4D.5
6.(2023春·浙江·九年级专题练习)抛物线与轴交于,两点,和也是抛物线上的点,且,,则下列判断正确的是( )
A.B.C.D.
7.(2022秋·浙江金华·九年级校考阶段练习)在平面直角坐标系中,将二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,将这个新函数的图象记为G(如图所示),当直线与图象G有4个交点时,则m的取值范围是( )
A.B.C.D.
8.(2022秋·浙江舟山·九年级校考阶段练习)已知关于x的一元二次方程有一个根是1,若的顶点在第一象限,设,则t的取值范围是( )
A. B.C. D.
9.(2022秋·浙江丽水·九年级期末)二次函数的部分对应值列表如下:
则一元二次方程的解为____________.
10.(2022秋·浙江杭州·九年级校考期中)抛物线的图象与轴交点的横坐标为和1,则不等式的解集是__________.
11.(2022秋·浙江宁波·九年级统考期中)如图, 抛物线与轴交于点, 顶点坐标为, 与轴的交点在之间 (包含端点), 则的取值范围为___________.
12.(2022秋·浙江绍兴·九年级统考期中)如图,在平面直角坐标系中,将二次函数在轴下方的图象沿轴翻折到轴上方,图象的其余部分不变,将这个新函数的图象记为.若直线与图象恰好有3个交点,则___________.
13.(2021·浙江金华·统考二模)在平面直角坐标系中,已知抛物线.
(1)若该抛物线过原点,则t的值为________.
(2)已知点与点,若该抛物线与线段只有一个交点,则t的范围是__.
14.(2022秋·浙江·九年级期中)对于一个函数,当自变量x取n时,函数值y等于2﹣n,我们称n为这个函数的“二合点”,如果二次函数y=ax2+x﹣1有两个相异的二合点x1,x2,且x1<x2<1,则a的取值范围是_____.
15.(2023·浙江杭州·校考二模)已知关于的二次函数.
(1)该函数的图象与轴只有一个交点,求与之间的关系;
(2)若,当时,随的增大而增大,求的范围;
(3)当,,该图象不经过第三象限,求的取值范围.
16.(2023·浙江杭州·统考二模)已知二次函数和一次函数.
(1)二次函数的图象过点,求二次函数的表达式;
(2)若一次函数与二次函数的图象交于x轴上同一点,且这个点不是原点.
①求证:;
②若两个函数图象的另一个交点为二次函数的顶点,求m的值.
17.(2023·浙江杭州·杭州市公益中学校考二模)在平面直角坐标系中,当和时,二次函数(,是常数,)的函数值相等.
(1)若该函数的最大值为,求函数的表达式,并写出函数图象的顶点坐标;
(2)若该函数的图象与轴有且只有一个交点,求,的值.
(3)记(2)中的抛物线为,将抛物线向上平移个单位得到抛物线,当时,抛物线的最大值与最小值之差为,求的值.
18.(2022秋·浙江温州·九年级校考期中)如图,在平面直角坐标系中,过点、两点的抛物线的顶点C在x轴正半轴上.
(1)求抛物线的解析式;
(2)求点C的坐标;
(3)为线段AB上一点,,作轴交抛物线于点M,求PM的最大值?
19.(2023秋·浙江绍兴·九年级统考期末)设二次函数(,是常数)的图像与轴交于,两点.
(1)若,两点的坐标分别为,,求该二次函数的表达式.
(2)若函数的表达式可以写成(是常数)的形式,求的最大值.
(3)设一次函数(是常数),若二次函数的表达式还可以写成的形式,当函数的图像经过点时,求的值.
20.(2022秋·浙江金华·九年级校联考阶段练习)学习完二次函数后,某班“数学兴趣小组”的同学对函数的图象和性质进行了探究,在经历列表、描点、连线步骤后得到其图象如图所示.
请根据函数图象完成以下问题:
(1)观察发现:
①写出该函数的一条性质_________________;
②函数图象与x轴有_________个交点,所以对应的方程有________个实数根;
(2)分析思考:
③方程的解为__________________;
④关于x的方程有4个实数根时,n的取值范围是_________;
(3)延伸探究:
⑤将函数的图象经过怎样的平移可以得到函数的图象,直接写出平移过程.
判别式
抛物线与x轴的交点
不等式的解集
不等式的解集
△>0
或
△=0
(或)
无解
△<0
全体实数
无解
…
4
0
1
2
3
4
…
…
5
0
0
1
0
…
0
1
2
3
3
0
0
3
x
…
0
1
3
5
…
y
…
7
7
…
专题17 比例线段重难点题型专训(6大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版): 这是一份专题17 比例线段重难点题型专训(6大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版),文件包含专题17比例线段重难点题型专训6大题型原卷版docx、专题17比例线段重难点题型专训6大题型解析版docx等2份试卷配套教学资源,其中试卷共67页, 欢迎下载使用。
专题14 弧长及扇形的面积重难点题型专训(七大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版): 这是一份专题14 弧长及扇形的面积重难点题型专训(七大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版),文件包含专题14弧长及扇形的面积重难点题型专训七大题型原卷版docx、专题14弧长及扇形的面积重难点题型专训七大题型解析版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
专题12 圆周角重难点题型专训(八大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版): 这是一份专题12 圆周角重难点题型专训(八大题型)-2023-2024学年九年级数学上册重难点高分突破(浙教版),文件包含专题12圆周角重难点题型专训八大题型原卷版docx、专题12圆周角重难点题型专训八大题型解析版docx等2份试卷配套教学资源,其中试卷共88页, 欢迎下载使用。












