


备战中考数学《重难点解读•专项训练》专题10 截长补短模型综合应用(专项训练)
展开一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度,培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准,安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础,在此基础上适当增加变式和难度,提高能力。
专题10 截长补短模型综合应用(专项训练)
(能力提升)
1.综合与实践
【问题情境】
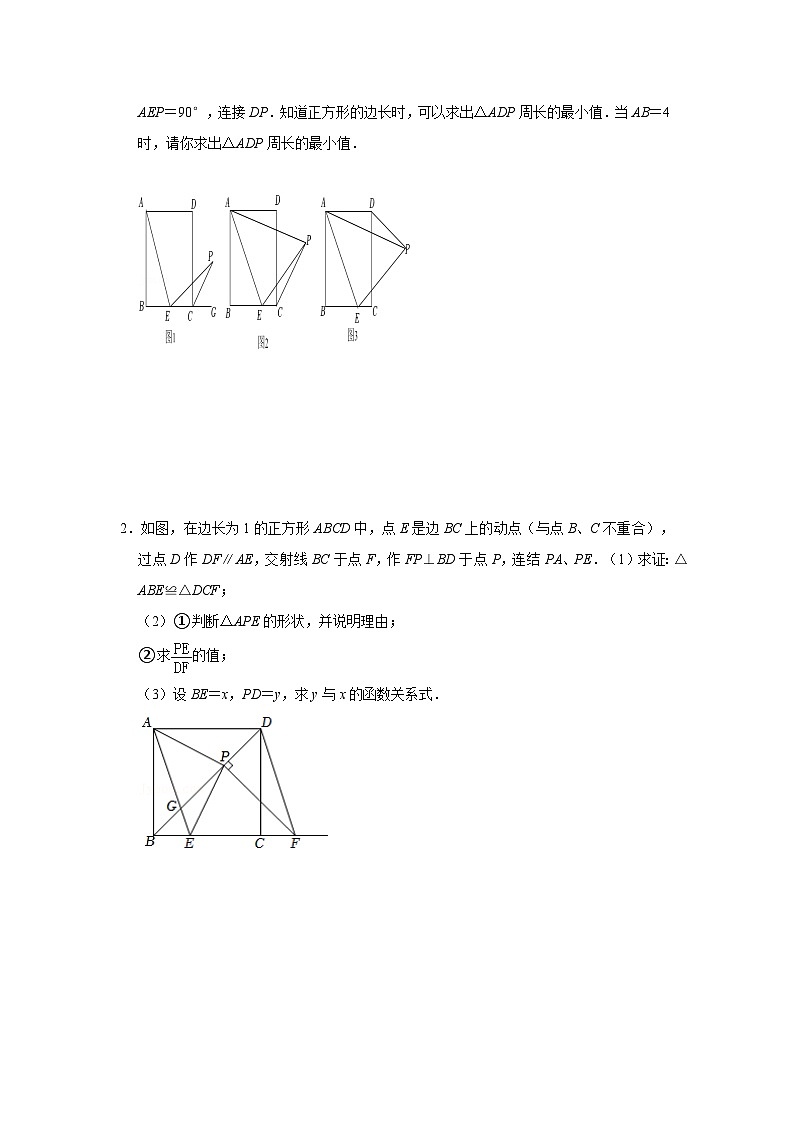
数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点,AE⊥EP,EP与正方形的外角∠DCG的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;
【思考尝试】
(1)同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
【实践探究】
(2)希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合),△AEP是等腰直角三角形,∠AEP=90°,连接CP,可以求出∠DCP的大小,请你思考并解答这个问题.
【拓展迁移】
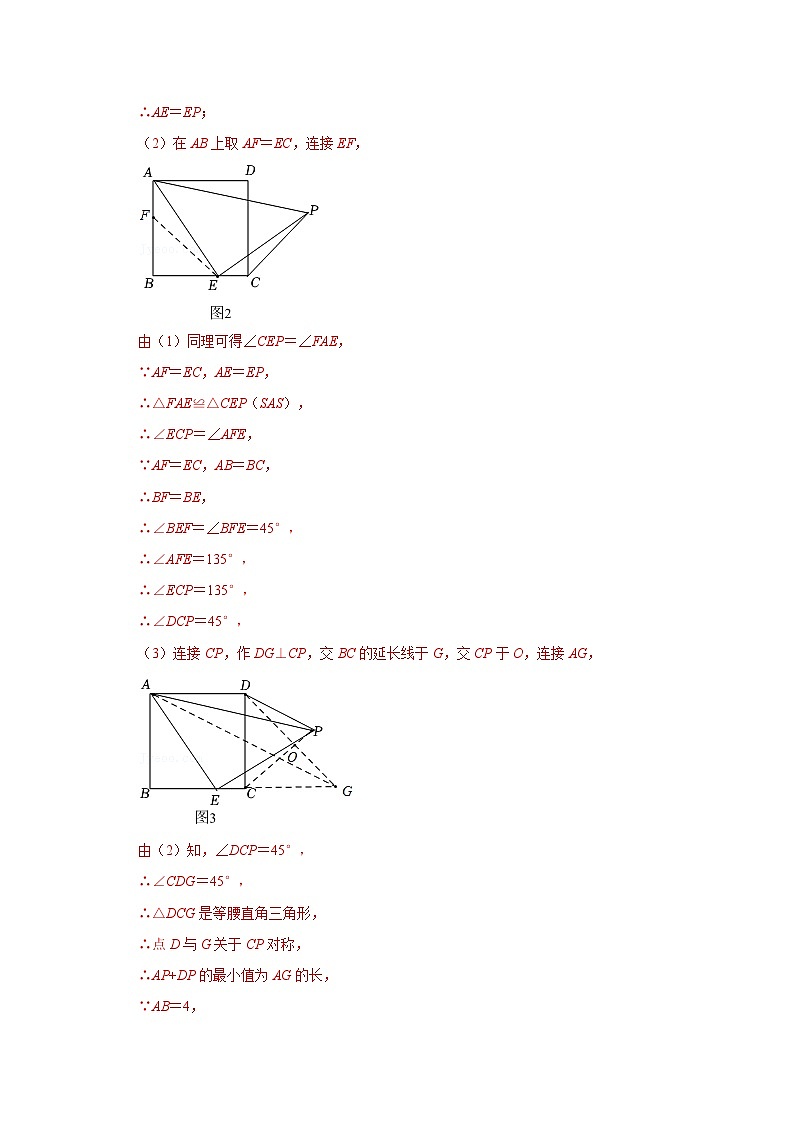
(3)突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合),△AEP是等腰直角三角形,∠AEP=90°,连接DP.知道正方形的边长时,可以求出△ADP周长的最小值.当AB=4时,请你求出△ADP周长的最小值.
【解答】解:(1)AE=EP,
理由如下:取AB的中点F,连接EF,
∵F、E分别为AB、BC的中点,
∴AF=BF=BE=CE,
∴∠BFE=45°,
∴∠AFE=135°,
∵CP平分∠DCG,
∴∠DCP=45°,
∴∠ECP=135°,
∴∠AFE=∠ECP,
∵AE⊥PE,
∴∠AEP=90°,
∴∠AEB+∠PEC=90°,
∵∠AEB+∠BAE=90°,
∴∠PEC=∠BAE,
∴△AFE≌△ECP(ASA),
∴AE=EP;
(2)在AB上取AF=EC,连接EF,
由(1)同理可得∠CEP=∠FAE,
∵AF=EC,AE=EP,
∴△FAE≌△CEP(SAS),
∴∠ECP=∠AFE,
∵AF=EC,AB=BC,
∴BF=BE,
∴∠BEF=∠BFE=45°,
∴∠AFE=135°,
∴∠ECP=135°,
∴∠DCP=45°,
(3)连接CP,作DG⊥CP,交BC的延长线于G,交CP于O,连接AG,
由(2)知,∠DCP=45°,
∴∠CDG=45°,
∴△DCG是等腰直角三角形,
∴点D与G关于CP对称,
∴AP+DP的最小值为AG的长,
∵AB=4,
∴BG=8,
由勾股定理得AG==4,
∴△ADP周长的最小值为AD+AG=4+4.
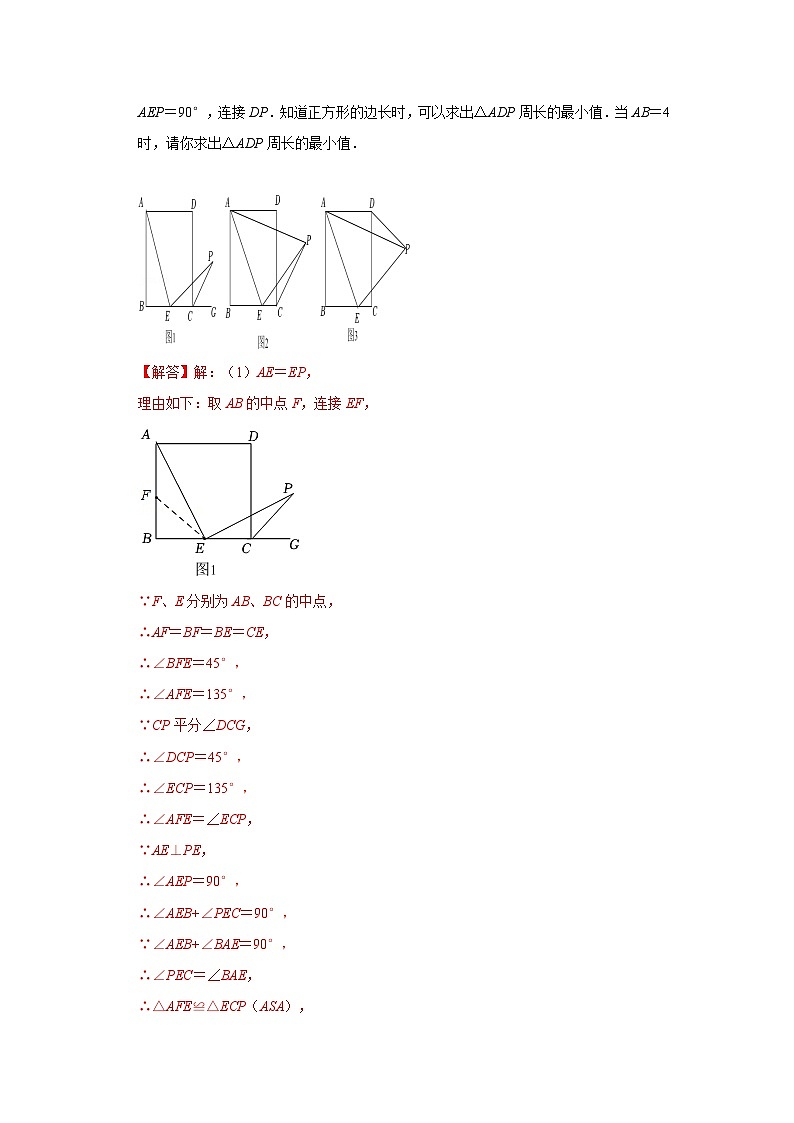
2.如图,在边长为1的正方形ABCD中,点E是边BC上的动点(与点B、C不重合),过点D作DF∥AE,交射线BC于点F,作FP⊥BD于点P,连结PA、PE.(1)求证:△ABE≌△DCF;
(2)①判断△APE的形状,并说明理由;
②求的值;
(3)设BE=x,PD=y,求y与x的函数关系式.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BCD=∠ABE=90°,AB=DC,
∴∠DCF=180°﹣∠BCD=90°,
∴∠ABE=∠DCF,
∵DF∥AE,
∴∠AEB=∠DFC,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS);
(2)解:①△APE是等腰直角三角形.理由如下:
如图,连接CP,
∵四边形ABCD是正方形,
∴∠ABD=∠CBD=45°,AB=BC,
∵BP=BP,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠APB=∠CPB,
∵FP⊥BD,∠PBF=45°,
∴△PBF是等腰直角三角形,
∴PB=PF,∠PFB=∠PBF=45°,
∵△ABE≌△DCF,
∴BE=CF,
∴△BEP≌△FCP(SAS),
∴PE=PC,∠BPE=∠FPC,
∴PA=PE,∠APE=∠APB+∠BPE=∠BPC+∠FPC=∠BPF=90°,
∴△APE是等腰直角三角形;
②∵△APE是等腰直角三角形,
∴=,
∵△ABE≌△DCF,
∴AE=DF,
∴==;
(3)设BE=x,PD=y,则BF=x+1,
∵△PBF是等腰直角三角形,
∴PB=(x+1),
∵BD=,
∴y=﹣(x+1),
即y=﹣x+(0<x<1).
3.我们定义:如图1,在△ABC中,把AC点绕点C顺时针旋转90°得到CA',把BC绕点C逆时针旋转90°得到CB′,连接A′B′.我们称△A′B′C是△ABC的“旋补交差三角形”,连接AB′、A′B,我们将AB′、A′B所在直线的相交而成的角称之为△ABC“旋补交差角”,C点到A′B′中点E间的距离成为“旋转中距”.如图1,∠B′OB即为△ABC“旋补交差角”,CE即为△ABC“旋补中距”.
(1)若已知图1中AB的长度等于4,当∠ACB=90°,则△ABC“旋补交差角”∠B′OB= 90° ,“旋补中距”CE长度= 2 ;
(2)若图1中∠ACB的度数发生改变,则△ABC“旋补交差角”度数是否发生改变?请证明你的结论,并直接判断△ABC“旋补中距”是否也发生改变;
(3)已知图2中△A′B′C是△ABC“旋补交差三角形”,AB的长度等于4,A′B′长度等于6,问OC是否存在最小值?如果存在,请求出具体的值,如果不存在,请说明理由.
【解答】解:(1)如图1,
∵把AC点绕点C顺时针旋转90°得到CA',把BC绕点C逆时针旋转90°得到CB′,
∴∠ACA'=90°=∠BCB',AC=A'C,BC=B'C,
∵∠ACB=90°,
∴∠A'CB'=∠ACB=90°,∠ACB+∠ACA'=180°,∠ACB+∠BCB'=180°,
∴点A,点C,点B'共线,点B,点C,点A'共线,
∴AB′、A′B的交点O与点C重合,
∴△ABC“旋补交差角”∠B′OB=90°,
∵AC=A'C,∠A'CB'=∠ACB=90°,BC=B'C,
∴△ACB≌△A'CB'(SAS),
∴AB=A'B'=4,
∵点E是A'B'的中点,∠A'CB'=90°,
∴CE=2,
故答案为:90°,2;
(2)△ABC“旋补交差角”度数不变,△ABC“旋补中距”长度不变,理由如下:
∵把AC点绕点C顺时针旋转90°得到CA',把BC绕点C逆时针旋转90°得到CB′,
∴∠ACA'=90°=∠BCB',AC=A'C,BC=B'C,
∴∠ACB'=∠BCA',
在△ACB'和△A'CB中,
,
∴△ACB'≌△A'CB(SAS),
∴∠CAB'=∠CA'B,
∴点A,点A',点C,点O四点共圆,
∴∠ACA'=∠AOA'=90°=∠BOB',
如图2,延长CE至F,使CE=EF,连接A'F,B'F,
∵CE=EF,A'E=B'E,
∴四边形A'CB'F是平行四边形,
∴∠A'CB'+∠FA'C=180°,A'F=B'C,
∵∠A'CB'+∠ACB=360°﹣∠A'CA﹣∠B'CB=180°,
∴∠ACB=∠CA'F,
又∵A'C=AC,A'F=B'C=BC,
∴△ACB≌△CA'F(SAS),
∴AB=CF=4,
∴CE=2;
(3)OC存在最小值,最小值为1,理由如下:
如图3,取A'B'中点E,连接CE,CO,EO,
∵△A′B′C是△ABC“旋补交差三角形”,
∴∠BOB'=90°,CE=AB=2,
∵点E是A'B'中点,∠A'OB'=90°,
∴OE=A'B'=3,
在△OCE中,OC>OE﹣CE,
∴当点C在线段OE上时,OC有最小值为OE﹣CE=1.
4.如图,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°(AB<AD),△ADE绕点A旋转.
(1)如图1,若连接BD,CE,则BD与CE的关系为 BD=CE,BD⊥CE ;
(2)如图2,若连接CD,BE,取BE中点F,连接AF,探究AF与CD的关系,并证明你的结论;
(3)在(2)的条件下,当△ADE旋转到如图3的位置时,点D落在BC延长线上,若AF=3,AC=,请直接写出线段AE的长.
【解答】解:(1)BD=CE,BD⊥CE,理由如下:
如图1,设CE与BD交于点O,
∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS),
∴BD=EC,∠ABD=∠ACE,
∵∠ABD+∠CBD+∠ACB=90°,
∴∠CBD+∠ACB+∠ACE=90°,
∴∠BOC=90°,
∴BD⊥CE,
故答案为:BD=CE,BD⊥CE;
(2)AF=CD,AF⊥CD,理由如下:
如图2,延长FA交DC于点G,延长AF到点H,使FH=FA,连接EH,
∵F是BE中点,
∴FE=FB,
又∵∠EFH=∠BFA,
∴△EFH≌△BFA(SAS),
∴HE=AB,∠HEB=∠EBA,
∴HE∥AB,
∴∠HEA+∠BAE=180°,
∵AB=AC,
∴HE=AC,
∵∠BAC=∠DAE=90°,
∴∠CAD+∠BAE=180°,
∴∠HEA=∠CAD,
又∵AD=AE,
∴△HEA≌△CAD(SAS),
∴AH=CD,∠EAH=∠ADC,
∵FH=FA,
∴AF=AH=CD,
∵∠DAE=90°,
∴∠EAH+∠DAG=90°,
∴∠ADC+∠DAG=90°,
∴∠AGD=90°,
∴AG⊥CD,
即AF⊥CD;
(3)如图3,过点A作AN⊥BC于N,
由(2)可知,CD=2AF=6,
∵AB=AC=4,∠BAC=90°,AN⊥BC,
∴BC=AB=8,AN=BC=BN=CN=4,
∴DN=CD+CN=10,
∴AD===2,
∴AE=AD=2.
5.(1)阅读理解:
如图①,在△ABC中,若AB=8,AC=5,求BC边上的中线AD的取值范围.
可以用如下方法:将△ACD绕着点D逆时针旋转180°得到△EBD,在△ABE中,利用三角形三边的关系即可判断中线AD的取值范围是 1 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=100°,以C为顶点作一个50°的角,角的两边分别交AB、AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并说明理由.
【解答】(1)解:如图①,将△ACD绕着点D逆时针旋转180°得到△EBD,则△ACD≌△EBD,
∴AD=DE,BE=AC=5,
在△ABE中,AB﹣BE<AE<AB+BE,即3<AE<13,
故答案为:1.5<AE<6.5;
(2)证明:如图②,延长FD至N,使DN=DF,连接BN、EN,
在△FDC和△NDB中,
,
∴△FDC≌△NDB(SAS)
∴BN=FC,
∵DF=DN,DE⊥DF,
∴EF=EN,
在△EBN中,BE+BN>EN,
∴BE+CF>EF;
(3)解:BE+DF=EF,
理由如下:如图③,延长AB至点H,使BH=DF,连接CH,
∵∠ABC+∠D=180°,∠HBC+∠ABC=180°,
∴∠HBC=∠D,
在△HBC和△FDC中,
,
∴△HBC≌△FDC(SAS)
∴CH=CF,∠HCB=∠FCD,
∵∠BCD=100°,∠ECF=50°,
∴∠BCE+∠FCD=50°,
∴∠ECH=50°=∠ECF,
在△HCE和△FCE中,
,
∴△HCE≌△FCE(SAS)
∴EH=EF,
∴BE+DF=EF.
6.阅读下面材料:
小军遇到这样一个问题:如图1,△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围.
小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.
请回答:AD的取值范围是 .
参考小军思考问题的方法,解决问题:
如图3,△ABC中,E为AB中点,P是CA延长线上一点,连接PE并延长交BC于点D.求证:PA•CD=PC•BD.
【解答】解:(1)1<AD<5,
延长AD到E,使DE=AD,连接BE,
在△ACD与△EBD中,,
∴△BDE≌△CDA,
∴BE=AC,
∴2<AE<10,
∴1<AD<5;
(2)证明:延长PD至点F,使EF=PE,连接BF,
∵BE=AE,∠BEF=∠AEP,
在△BEF与△AEP中,,
∴△BEF≌△AEP,
∴∠APE=∠F,BF=PA,
又∵∠BDF=∠CDP,
∴△BDF∽△CDP,
∴=,
∴=,
即PA•CD=PC•BD.
7.【阅读理解】
截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是 ;
【拓展延伸】
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
【知识应用】
(3)如图3,两块斜边长都为14cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长为 cm.
【解答】解:(1)如图1,延长DC到点E,使CE=BD,连接AE,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠BDC=120°,
∴∠ABD+∠ACD=180°,
又∵∠ACE+∠ACD=180°,
∴∠ABD=∠ACE,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
∵∠ABC=60°,即∠BAD+∠DAC=60°,
∴∠DAC+∠CAE=60°,即∠DAE=60°,
∴△ADE是等边三角形,
∴DA=DE=DC+CE=DC+DB,即DA=DC+DB,
故答案为:DA=DC+DB;
(2)DA=DB+DC,
如图2,延长DC到点E,使CE=BD,连接AE,
∵∠BAC=90°,∠BDC=90°,
∴∠ABD+∠ACD=180°,
∵∠ACE+∠ACD=180°,
∴∠ABD=∠ACE,
∵AB=AC,CE=BD,
∴△ABD≌△ACE,
∴AD=AE,∠BAD=∠CAE,
∴∠DAE=∠BAC=90°,
∴DA2+AE2=DE2,
∴2DA2=(DB+DC)2,
∴DA=DB+DC;
(3)如图3,连接PQ,
∵MN=14,∠QMN=30°,
∴QN=MN=7,
∴MQ===7,
由(2)知PQ=QN+QM=7+7,
∴PQ==,
故答案为:.
8.截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是;(直接写出结果)
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.
【解答】解:(1)结论:DA=DB+DC.
理由:如图1,延长DC到点E,使CE=BD,连接AE,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠BDC=120°,
∴∠ABD+∠ACD=180°,
又∵∠ACE+∠ACD=180°,
∴∠ABD=∠ACE,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
∵∠ABC=60°,即∠BAD+∠DAC=60°,
∴∠DAC+∠CAE=60°,即∠DAE=60°,
∴△ADE是等边三角形,
∴DA=DE=DC+CE=DC+DB,即DA=DC+DB,
(2)结论:DA=DB+DC,
理由:如图2,延长DC到点E,使CE=BD,连接AE,
∵∠BAC=90°,∠BDC=90°,
∴∠ABD+∠ACD=180°,
∵∠ACE+∠ACD=180°,
∴∠ABD=∠ACE,
∵AB=AC,CE=BD,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
∴∠DAE=∠BAC=90°,
∴DA2+AE2=DE2,
∴2DA2=(DB+DC)2,
∴DA=DB+DC;
备战中考数学《重难点解读•专项训练》专题06 半角模型综合应用(专项训练): 这是一份备战中考数学《重难点解读•专项训练》专题06 半角模型综合应用(专项训练),文件包含专题06半角模型综合应用专项训练原卷版docx、专题06半角模型综合应用专项训练解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
备战中考数学《重难点解读•专项训练》专题05 对角互补模型综合应用(专项训练): 这是一份备战中考数学《重难点解读•专项训练》专题05 对角互补模型综合应用(专项训练),文件包含专题05对角互补模型综合应用专项训练原卷版docx、专题05对角互补模型综合应用专项训练解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
专题10 截长补短模型综合应用(知识解读)-备战中考数学《重难点解读•专项训练》(全国通用): 这是一份专题10 截长补短模型综合应用(知识解读)-备战中考数学《重难点解读•专项训练》(全国通用),文件包含专题10截长补短模型综合应用知识解读-备战中考数学《重难点解读•专项训练》全国通用解析版docx、专题10截长补短模型综合应用知识解读-备战中考数学《重难点解读•专项训练》全国通用原卷版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。












