

备战中考数学《重难点解读•专项训练》专题05 对角互补模型综合应用(知识解读)
展开一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度,培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准,安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础,在此基础上适当增加变式和难度,提高能力。
专题05 对角互补模型综合应用(知识解读)
【专题说明】
共顶点模型,即四边形或构成的几何图形中,相对的角互补。主要:含90°的对角互补,含120°的对角互补,两种类型,种类不同,得出的个别结论会有所区别。解决此类题型常用到的辅助线画法主要有两种:旋转法和过顶点作两垂线.
【方法技巧】
类型一:含90°的对角互补模型
(1)如图,∠AOB=∠DCE=90°,OC平分∠AOB,则有以下结论:
作法1 作法2
;
;
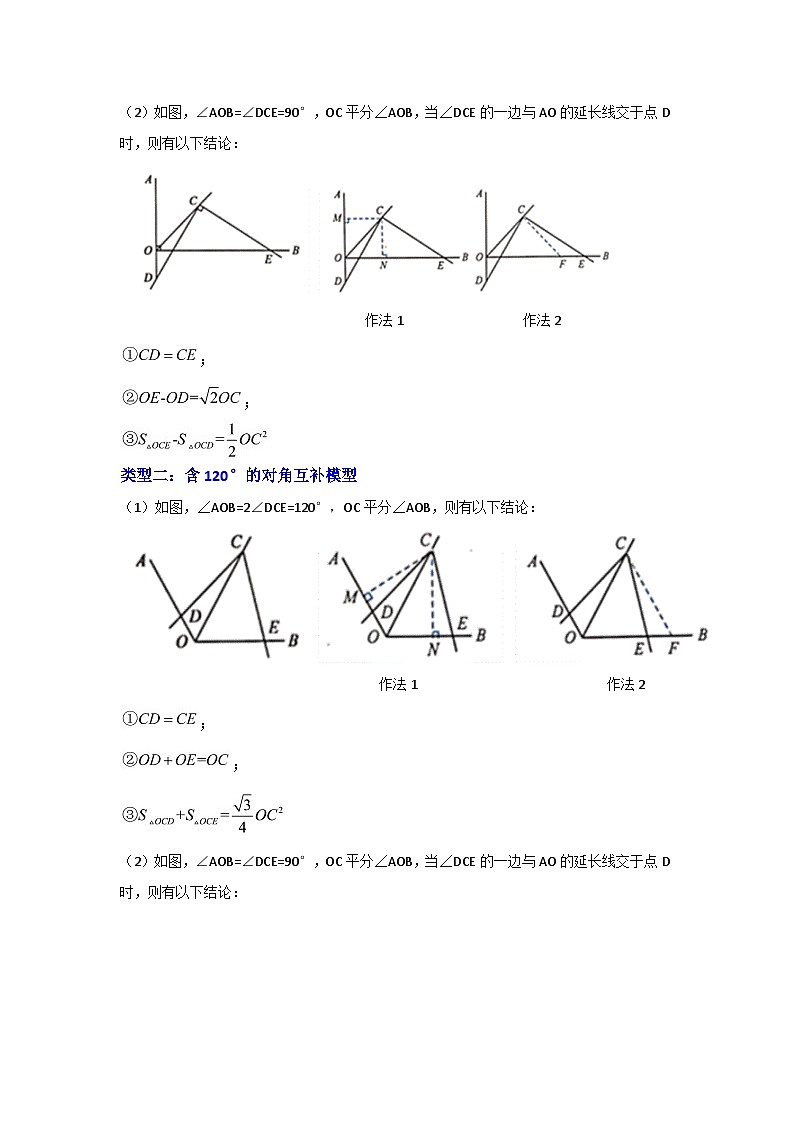
(2)如图,∠AOB=∠DCE=90°,OC平分∠AOB,当∠DCE的一边与AO的延长线交于点D时,则有以下结论:
作法1 作法2
;
;
类型二:含120°的对角互补模型
(1)如图,∠AOB=2∠DCE=120°,OC平分∠AOB,则有以下结论:
作法1 作法2
;
;
(2)如图,∠AOB=∠DCE=90°,OC平分∠AOB,当∠DCE的一边与AO的延长线交于点D时,则有以下结论:
作法1 作法2
;
;
【典例分析】
【类型一:含90°的对角互补模型】
【典例1】(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是 ;(不需要证明)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
【变式1-1】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,连接EF交AP于点G,以下五个结论:①∠B=∠C=45°;②AP=EF;③∠AFP和∠AEP互补;④△EPF是等腰直角三角形;⑤四边形AEPF的面积是△ABC面积的,其中正确的结论是( )
A.①②③B.①②④⑤C.①③④⑤D.①③④
【变式1-2】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=50°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论是 (直接写结论,不需证明);
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且2∠EAF=∠BAD,上述结论是否仍然成立,若成立,请证明,若不成立,请说明理由;
(3)如图3,四边形ABCD是边长为7的正方形,∠EBF=45°,直接写出△DEF的周长.
【变式1-3】(1)如图①,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.请直接写出线段EF,BE,FD之间的数量关系: ;
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?请写出证明过程;
(3)在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD所在直线上的点,且∠EAF=∠BAD.请直接写出线段EF,BE,FD之间的数量关系: .
【变式1-4】问题探究:如图1,在△ABC中,点D是BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①BE、CF与EF之间的关系为:BE+CF EF;(填“>”、“=”或“<”)
②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.
问题解决:如图2,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=130°,以D为顶点作∠EDF=65°,∠EDF的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【类型二:含120°的对角互补模型】
【典例2】问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
【变式2-1】如图,△ABC是边长为6的等边三角形,BD=CD,∠BDC=120°,以点D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连结MN,则△AMN的周长是 .
【变式2-2】【问题背景】
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 .
【探索延伸】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.
【学以致用】
如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出△DEF的周长.
专题05 对角互补模型综合应用(知识解读)
【专题说明】
共顶点模型,即四边形或构成的几何图形中,相对的角互补。主要:含90°的对角互补,含120°的对角互补,两种类型,种类不同,得出的个别结论会有所区别。解决此类题型常用到的辅助线画法主要有两种:旋转法和过顶点作两垂线.
【方法技巧】
类型一:含90°的对角互补模型
(1)如图,∠AOB=∠DCE=90°,OC平分∠AOB,则有以下结论:
作法1 作法2
;
;
(2)如图,∠AOB=∠DCE=90°,OC平分∠AOB,当∠DCE的一边与AO的延长线交于点D时,则有以下结论:
作法1 作法2
;
;
类型二:含120°的对角互补模型
(1)如图,∠AOB=2∠DCE=120°,OC平分∠AOB,则有以下结论:
作法1 作法2
;
;
(2)如图,∠AOB=∠DCE=90°,OC平分∠AOB,当∠DCE的一边与AO的延长线交于点D时,则有以下结论:
作法1 作法2
;
;
【典例分析】
【类型一:含90°的对角互补模型】
【典例1】(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是 ;(不需要证明)
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
【解答】解:(1)EF=BE+FD,
理由如下:如图1,延长CB至G,使BG=DF,连接AG,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵∠EAF=∠BAD,
∴∠DAF+∠BAE=∠EAF,
∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠EAF,
在△GAE和△FAE中,
,
∴△GAE≌△FAE(SAS),
∴EF=EG,
∵EG=BG+BE=BE+DF,
∴EF=BE+FD,
故答案为:EF=BE+FD;
(2)(1)中的结论仍然成立,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠1=180°,
∴∠1=∠D,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠3=∠2,
∵∠EAF=∠BAD,
∴∠3+∠4=∠EAF,
∴∠EAM=∠3+∠4=∠2+∠4=∠EAF,
在△MAE和△FAE中,
,
∴△MAE≌△FAE(SAS),
∴EF=EM,
∵EM=BM+BE=BE+DF,
∴EF=BE+FD;
(3)(1)中的结论不成立,EF=BE﹣FD,
理由如下:如图3,在EB上截取BH=DF,连接AH,
同(2)中证法可得,△ABH≌△ADF,
∴AH=AF,∠BAH=∠DAF,
∴∠HAE=∠FAE,
在△HAE和△FAE中,
,
∴△HAE≌△FAE(SAS),
∴EF=EH,
∵EH=BE﹣BH=BE﹣DF,
∴EF=BE﹣FD.
【变式1-1】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,连接EF交AP于点G,以下五个结论:①∠B=∠C=45°;②AP=EF;③∠AFP和∠AEP互补;④△EPF是等腰直角三角形;⑤四边形AEPF的面积是△ABC面积的,其中正确的结论是( )
A.①②③B.①②④⑤C.①③④⑤D.①③④
【答案】D
【解答】解:∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
故①正确;
∵点P为BC的中点,∠BAC=90°,AB=AC,
∴AP=CP,∠APC=90°,∠BAP=∠C=45°,
∵∠EPF=∠APC,
∴∠APE=∠FPC,
在△AEP和△CFP中,
,
∴△AEP≌△CFP(ASA),
∴PE=PF,
∴△EPF是等腰直角三角形,
∴四边形AEPF的面积为S△AEP+S△AFP=S△CPF+S△APF=S△APC=S△ABC,
故④正确,⑤不正确;
∵∠BAC=∠EPF=90°,
∴∠AFP和∠AEP互补,
故③正确;
∵PE不是定长,故②不正确.
∴正确的有:①③④,
故选:D.
【变式1-2】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=50°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论是 EF=BE+DF (直接写结论,不需证明);
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且2∠EAF=∠BAD,上述结论是否仍然成立,若成立,请证明,若不成立,请说明理由;
(3)如图3,四边形ABCD是边长为7的正方形,∠EBF=45°,直接写出△DEF的周长.
【解答】证明:(1)延长FD到点G.使DG=BE.连接AG,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠BAD=100°,∠EAF=50°,
∴∠BAE+∠FAD=∠DAG+∠FAD=50°,
∴∠EAF=∠FAG=50°,
在△EAF和△GAF中,
∵,
∴△EAF≌△GAF(SAS),
∴EF=FG=DF+DG,
∴EF=BE+DF,
故答案为:EF=BE+DF;
(2)结论仍然成立,
理由如下:如图2,延长EB到G,使BG=DF,连接AG.
∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,
∴∠ABG=∠D,
∵在△ABG与△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵2∠EAF=∠BAD,
∴∠DAF+∠BAE=∠BAG+∠BAE=∠BAD=∠EAF,
∴∠GAE=∠EAF,
又AE=AE,
∴△AEG≌△AEF(SAS),
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD;
(3)如图,延长EA到H,使AH=CF,连接BH,
∵四边形ABCD是正方形,
∴AB=BC=7=AD=CD,∠BAD=∠BCD=90°,
∴∠BAH=∠BCF=90°,
又∵AH=CF,AB=BC,
∴△ABH≌△CBF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠EBF=45°,
∴∠CBF+∠ABE=45°=∠HBA+∠ABE=∠EBF,
∴∠EBH=∠EBF,
又∵BH=BF,BE=BE,
∴△EBH≌△EBF(SAS),
∴EF=EH,
∴EF=EH=AE+CF,
∴△DEF的周长=DE+DF+EF=DE+DF+AE+CF=AD+CD=14.
【变式1-3】(1)如图①,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.请直接写出线段EF,BE,FD之间的数量关系: ;
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?请写出证明过程;
(3)在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD所在直线上的点,且∠EAF=∠BAD.请直接写出线段EF,BE,FD之间的数量关系: .
【解答】解:(1)如图1,延长EB到G,使BG=DF,连接AG.
∵在△ABG与△ADF中,
,
∴△ABG≌△ADF(SAS).
∴AG=AF,∠1=∠2,
∴∠1+∠3=∠2+∠3=∠BAD=∠EAF.
∴∠GAE=∠EAF.
又AE=AE,
易证△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD
(2)(1)中的结论EF=BE+FD仍然成立.
理由是:如图2,延长EB到G,使BG=DF,连接AG.
∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,
∴∠ABG=∠D,
∵在△ABG与△ADF中,
,
∴△ABG≌△ADF(SAS).
∴AG=AF,∠1=∠2,
∴∠1+∠3=∠2+∠3=∠BAD=∠EAF.
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD
(3)当(1)结论EF=BE+FD成立,
当图三中,EF=BE﹣FD或EF=FD﹣BE.
证明:在BE上截取BG,使BG=DF,连接AG.
∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,
∴∠B=∠ADF.
∵在△ABG与△ADF中,
,
∴△ABG≌△ADF(SAS).
∴∠BAG=∠DAF,AG=AF.
∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=∠BAD.
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF(SAS).
∴EG=EF
∵EG=BE﹣BG
∴EF=BE﹣FD.
同理可得:∴EG=EF
∵EG=BG﹣BE
∴EF=FD﹣BE.
故答案为:(1)EF=BE+FD;(2)成立;(3)EF=BE+FD或EF=BE﹣FD或EF=FD﹣BE.
\
【变式1-4】问题探究:如图1,在△ABC中,点D是BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①BE、CF与EF之间的关系为:BE+CF EF;(填“>”、“=”或“<”)
②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.
问题解决:如图2,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=130°,以D为顶点作∠EDF=65°,∠EDF的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【解答】解:(1)如图1中,延长ED到H,使得DH=DE,连接CH,FH.
∵BD=CD,∠BDE=∠CDH,DE=DH,
∴△BDE≌△CDH(SAS),
∴BE=CH,
∵DE=DH,FD⊥EH,
∴FE=FH,
在△FCH中,∵CH+CF>FH,
∴BE+CF>EF.
故答案为>.
(2)结论:EF2=BE2+CF2.
理由:如图2中,延长ED到H,使得DH=DE,连接CH,FH.
∵BD=CD,∠BDE=∠CDH,DE=DH,
∴△BDE≌△CDH(SAS),
∴BE=CH,∠B=∠DCH,
∵DE=DH,FD⊥EH,
∴FE=FH,
∵∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCH=90°,
∴∠FCH=90°,
∴FH2=CH2+CF2,
∴EF2=BE2+CF2.
(3)如图3中,结论:EF=BE+CF.
理由:∵DB=DC,∠B+∠ACD=180°,
∴可以将△DBE绕点D顺时针旋转得到△DCH,A,C,H共线.
∵∠BDC=130°,∠EDF=65°,
∴∠CDH+∠CDF=∠BDE+∠CDF=65°,
∴∠FDE=∠FDH,
∵DF=DF,DE=DH,
∴△FDE≌△FDH(SAS),
∴EF=FH,
∵FH=CF+CH=CF+BE,
∴EF=BE+CF.
【类型二:含120°的对角互补模型】
【典例2】问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
【解答】解:问题背景:由题意:△ABE≌△ADG,△AEF≌△AGF,
∴BE=DG,EF=GF,
∴EF=FG=DF+DG=BE+FD.
故答案为:EF=BE+FD.
探索延伸:EF=BE+FD仍然成立.
理由:如图2,延长FD到点G,使DG=BE,连接AG
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG,
又∵AB=AD,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
又∵∠EAF=∠BAD,
∴∠FAG=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD﹣∠EAF,
=∠BAD﹣∠BAD=∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
又∵FG=DG+DF=BE+DF,
∴EF=BE+FD.
实际应用:如图3,连接EF,延长AE,BF相交于点C,
在四边形AOBC中,
∵∠AOB=30°+90°+20°=140°,∠FOE=70°=∠AOB,
又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的条件,
∴结论EF=AE+FB成立.
即,EF=AE+FB=2×(70+90)=320(海里)
答:此时两舰艇之间的距离为320海里.
【变式2-1】如图,△ABC是边长为6的等边三角形,BD=CD,∠BDC=120°,以点D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连结MN,则△AMN的周长是 .
【解答】解:∵△BDC是等腰三角形,且∠BDC=120°,
∴∠BCD=∠DBC=30°,
∵△ABC是边长为4的等边三角形,
∴∠ABC=∠BAC=∠BCA=60°,
∴∠DBA=∠DCA=90°,
延长AB至F,使BF=CN,连接DF,
在△BDF和△CND中,
,
∴△BDF≌△CND(SAS),
∴∠BDF=∠CDN,DF=DN,
∵∠MDN=60°,
∴∠BDM+∠CDN=60°,
∴∠BDM+∠BDF=60°,
在△DMN和△DMF中,
,
∴△DMN≌△DMF(SAS),
∴MN=MF,
∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6+6=12.
故答案为:12.
【变式2-2】【问题背景】
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 .
【探索延伸】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.
【学以致用】
如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出△DEF的周长.
【解答】(1)解:如图1,
在△ABE和△ADG中,
∵,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF.
(2)解:结论EF=BE+DF仍然成立;
理由:如图2,延长FD到点G.使DG=BE.连接AG,
在△ABE和△ADG中,
∵,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)解:如图3,延长DC到点G,截取CG=AE,连接BG,
在△AEB与△CGB中,
∵,
∴△AEB≌△CGB(SAS),
∴BE=BG,∠ABE=∠CBG.
∵∠EBF=45°,∠ABC=90°,
∴∠ABE+∠CBF=45°,
∴∠CBF+∠CBG=45°.
在△EBF与△GBF中,
∵,
∴△EBF≌△GBF(SAS),
∴EF=GF,
∴△DEF的周长=EF+ED+DF=AE+CF+DE+DF=AD+CD=5+5=10.
备战中考数学《重难点解读•专项训练》专题05 对角互补模型综合应用(专项训练): 这是一份备战中考数学《重难点解读•专项训练》专题05 对角互补模型综合应用(专项训练),文件包含专题05对角互补模型综合应用专项训练原卷版docx、专题05对角互补模型综合应用专项训练解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
备战中考数学《重难点解读•专项训练》专题05 对角互补模型综合应用(能力提升): 这是一份备战中考数学《重难点解读•专项训练》专题05 对角互补模型综合应用(能力提升),文件包含专题05对角互补模型综合应用能力提升原卷版docx、专题05对角互补模型综合应用能力提升解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
2024年中考数学专题训练 专题05 对角互补模型综合应用(知识解读): 这是一份2024年中考数学专题训练 专题05 对角互补模型综合应用(知识解读),共27页。












