备战中考数学《重难点解读•专项训练》专题13 最值模型：瓜豆原理-主从动点问题（专项训练）

这是一份备战中考数学《重难点解读•专项训练》专题13 最值模型：瓜豆原理-主从动点问题（专项训练），文件包含专题13最值模型瓜豆原理-主从动点问题专项训练-备战2023年中考数学《重难点解读•专项训练》全国通用原卷版docx、专题13最值模型瓜豆原理-主从动点问题专项训练-备战2023年中考数学《重难点解读•专项训练》全国通用解析版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。

一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度，培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准，安排时间要合理。
2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础，在此基础上适当增加变式和难度，提高能力。

专题13 最值模型；瓜豆原理-主
从动点问题（专项训练）
1．如图，矩形ABCD中，AD＝6，DC＝8，点E为对角线AC上一动点，BE⊥BF，，BG⊥EF于点G，连接CG，当CG最小时，CE的长为 ．
【答案】
【解答】解：如图，过点B作BP⊥AC于点P，连接PG，
∵，∠ABC＝∠EBF，
∴△ABC∽△EBF，
∴∠CAB＝∠FEB，
∵∠APB＝∠EGB＝90°，
∴△ABP∽△EBG，
∴＝，∠ABP＝∠EBG，
∴∠ABE＝∠PBG，
∴△ABE∽△PBG，
∴∠BPG＝∠BAE，
即在点E的运动过程中，∠BPG的大小不变且等于∠BAC，
∴当CG⊥PG时，CG最小，
设此时AE＝x，
∵，
∴PG＝，
∵CG⊥PG，
∴∠PCG＝∠BPG＝∠BAC，
∴，
代入PG＝，解得CP＝x，
∵CP＝BC•sin∠CBP＝BC•sin∠BAC＝，
∴x＝，
∴AE＝．
∴CE＝，
故答案为：．
2．如图，在△ABC中，AB＝AC，BC＝6，tan∠ACB＝2，点P在边AC上运动（可与点A，C重合），将线段BP绕点P逆时针旋转120°，得到线段DP，连接BD，CD，则CD长的最小值为 ．
【答案】
【解答】解：如图所示，以BC为底边向上作等腰△BQC，使∠BQC＝120°，连接PQ．
由题意可得△BQC和△BPD均为顶角为120° 的等腰三角形，
可得，∠QBC＝∠PBD＝30°，
∴∠QBC﹣∠QBD＝∠PBD﹣∠QBD，
∴∠PBQ＝∠DBC，
∴△PBQ∽△DBC，
∴，
∴当PQ⊥AC时，有PQ最小，即此时CD最小，
如图所示，设OP′⊥AC，延长AQ与BC交K，此时QP'为QP的最小值，
可得AK⊥BC，
∵△BQC中，∠BQC＝120°，BC＝6，
∴BK＝3，∠QBK＝30°，
∴QK＝＝，
∵tan∠ACB＝＝，KC＝3，
∴AK＝＝，
∴AQ＝AK﹣QK＝，AC＝＝，
∵∠AP'Q＝∠AKC＝90°，∠QAP'＝∠CAK，
∴△AQP'∽△ACK，
∴，
∴，
∴QP'＝，
∴CD＝＝．
3．如图，在△ABC中，∠ACB＝90°，点D在BC边上，BC＝5，CD＝2，点E是边AC所在直线上的一动点，连接DE，将DE绕点D顺时针方向旋转60°得到DF，连接BF，则BF的最小值为 ．
【答案】
【解答】解：如图，以BD为边作等边三角形DBH，连接EH，过点H作HN⊥BD于N，
∵BC＝5，CD＝2，
∴BD＝3，
∵△DHB是等边三角形，HN⊥BD，
∴DN＝BN＝，DB＝DH，∠HDB＝60°，
∴CN＝，
∵将DE绕点D顺时针方向旋转60°得到DF，
∴DE＝DF，∠EDF＝60°，
∴∠EDF＝∠HDB，
∴∠EDH＝∠FDB，
在△DHE和△DBF中，
，
∴△DHE≌△DBF（SAS），
∴EH＝BF，
∴当EH有最小值时，BF有最小值，
由垂线段最短可得：当EH⊥AC时，EH有最小值，
此时，∵EH⊥AC，∠ACB＝90°，HN⊥DB，
∴四边形CNHE是矩形，
∴HE＝CN＝，
故答案为：．
4．如图，在矩形ABCD中，对角线AC，BD相交于点O，AB＝6，∠DAC＝60°，点F在线段AO上从点A至点O运动，连接DF，以DF为边作等边三角形DFE，点E和点A分别位于DF两侧，则点E运动的路程长是 ．
【答案】2
【解答】解：连接OE，
∵四边形ABCD是矩形，
∴AO＝DO，∠DAB＝90°，
∵∠DAC＝60°，
∴△DAO是等边三角形，
∴DA＝DO，∠ADO＝60°，
∵△DFE是等边三角形，
∴DE＝DF，∠EDF＝60°，
∴∠ADF＝∠ODE，
又AD＝DO，DF＝DE，
∴△ADF≌△ODE（SAS），
∴OE＝AF，∠DOE＝∠DAO，
∴点E在射线OE上运动，且OE＝AF，
当点F在线段AO上从点A至点O运动时，
∴点E的运动路程是AO，
在Rt△ADB中，设AD＝x，则BD＝2x，
∴（2x）2﹣x2＝62，
解得x＝2（负值舍去），
∴AD＝AO＝2，
即点E的运动路程为2，
故答案为：2．
5．如图，正方形ABCD的边长为7，E为BC上一点，且BE＝，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为 ．
【答案】2
【解答】解：∵△EFG为等边三角形，
∴EF＝EG，
把△EBF绕点E顺时针旋转60°得到△EHG，如图，延长HG交CD于M，过C点作CQ⊥HM，过E点作EP⊥CQ，
∴∠BEH＝60°，EB＝EH＝，∠EHG＝∠EBF＝90°，
即G点在过H点且垂直于EH的线段HM上，
易得四边形HEPQ为矩形，
∴PQ＝EH＝，∠HEP＝90°，
∵∠CEP＝90°﹣∠BEH＝30°，
∴CP＝CE＝，
∴CQ＝CP+PQ＝+＝．
∴CG的最小值为．
故答案为．
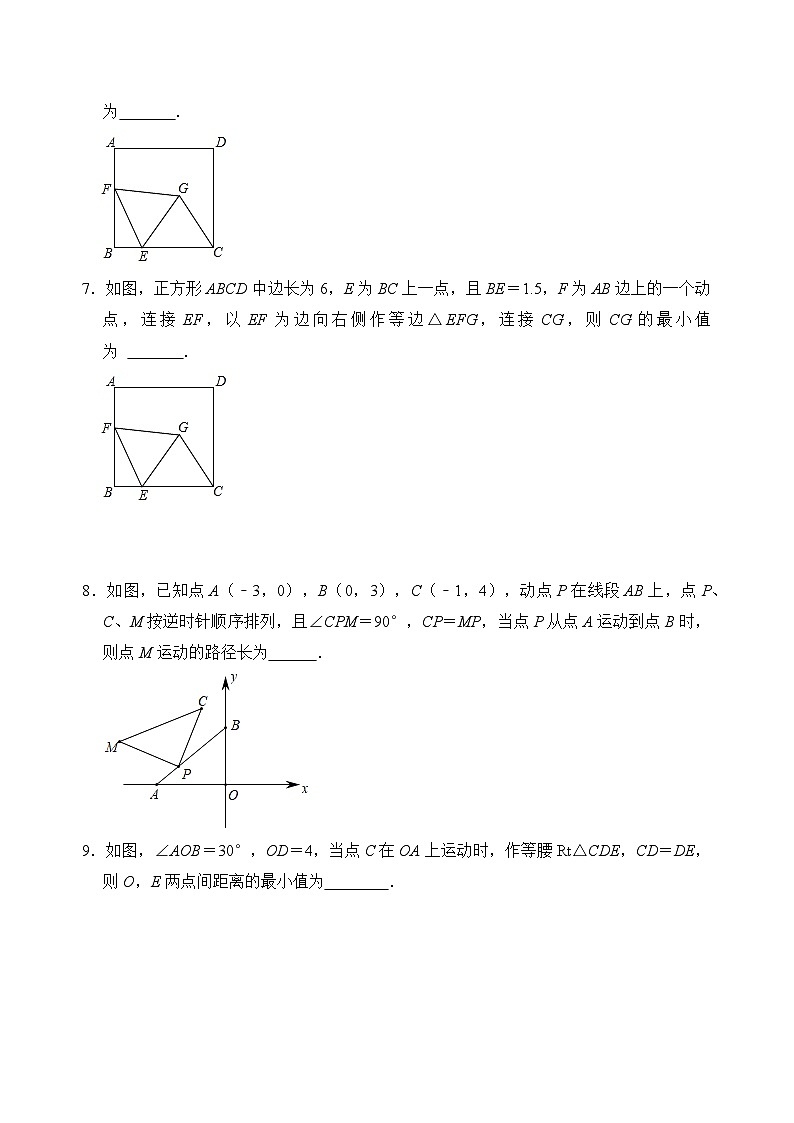
6．如图，正方形ABCD的边长为8，E为BC上一点，且BE＝2.5，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为 ．
【答案】
【解答】解：由题意可知，点F是主动点，点G是从动点，点F在线段上运动，点G也一定在直线轨迹上运动，
将△EFB绕点E旋转60°，使EF与EG重合，得到△EFB≌△EHG，
从而可知△EBH为等边三角形，点G在垂直于HE的直线HN上，
过点C作CM⊥HN，则CM即为CG的最小值，
过点E作EP⊥CM，可知四边形HEPM为矩形，
则CM＝MP+CP＝HE+EC＝2.5+＝，
故答案为：．
7．如图，正方形ABCD中边长为6，E为BC上一点，且BE＝1.5，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为 ．
【答案】
【解答】解：如图，以EC为边作等边三角形ECH，过点H作HN⊥BC于N，HM⊥⊥AB于M，
又∵∠ABC＝90°，
∴四边形MHNB是矩形，
∴MH＝BN，
∵BE＝1.5，
∴EC＝，
∵△EHC是等边三角形，HN⊥EC，
∴EC＝EH＝，EN＝NC＝，∠HEC＝60°，
∴BN＝＝MH，
∵△FGE是等边三角形，
∴FE＝GE，∠FEG＝60°＝∠HEC，
∴∠FEH＝∠GEC，
在△FEH和△GEC中，
，
∴△FEH≌△GEC（SAS），
∴FH＝GC，
∴当FH⊥AB时，FH有最小值，即GC有最小值，
∴点F与点M重合时，FH＝HM＝，
故答案为．
8．如图，已知点A（﹣3，0），B（0，3），C（﹣1，4），动点P在线段AB上，点P、C、M按逆时针顺序排列，且∠CPM＝90°，CP＝MP，当点P从点A运动到点B时，则点M运动的路径长为 ．
【答案】6
【解答】解：∵点A（﹣3，0），B（0，3），
∴AB＝，
∵C（﹣1，4），动点P在线段AB上，∠CPM＝90°，CP＝MP，
∴，P为主动点，M为从动点，C为定点，
由“瓜豆原理”得P运动路径（AB）与M运动路径之比等于，
∴点M运动的路径长为÷＝6，
故答案为：6．
9．如图，∠AOB＝30°，OD＝4，当点C在OA上运动时，作等腰Rt△CDE，CD＝DE，则O，E两点间距离的最小值为 ．
【答案】2+2
【解答】解：∵∠AOB＝30°，OD＝4，点C在OA上运动时，CD＝DE，CD⊥DE，
∴C为主动点，E为从动点，D为定点，
由“瓜豆原理”，C在OA上运动，则E在垂直OA的直线上运动，
当DC⊥OA时，如答图：
过E作EM⊥OA于M，交OB于N，则直线MN即为E的运动轨迹，OM的长为O，E两点间距离的最小值，
∵∠AOB＝30°，OD＝4，DC⊥OA，
∴CD＝2，
∵CD＝DE，
∴DE＝2，
∵∠OCD＝∠CDE＝90°，
∴DE∥OA，
而EM⊥OA，
∴∠DEN＝90°，∠EDN＝30°，
∴在△DEN中可得DN＝，
∴ON＝4+，
△OMN中可得OM＝×（4+）＝2+2，
故答案为：2+2．
10．如图，正方形ABCD的边长为2，E为BC上一点，且BE＝1，F为AB边上的一个动点，连接EF，以EF为底向右侧作等腰直角△EFG，连接CG，则CG的最小值为 ．
【答案】
【解答】解：如图1，过点G作GP⊥AB于点P，GQ⊥BC于点Q，连接BD，
根据题意知，∠ABC＝90°，∠PGQ＝90°．
∴∠PGF+∠FGQ＝∠QGE+∠FGQ＝90°．
∴∠PGF＝∠QGE．
又∵△EFG是等腰直角三角形，且∠FGE＝90°，
∴GF＝GE．
在△GPF与△GQE中，
，
∴△GPF≌△GQE（AAS）．
∴GP＝GQ，∠GBP＝∠GBE＝∠ABC．
∴点G在BD所在的直线上运动．
∵F为AB边上的一个动点，如图2，
当点F与点B重合时，点G的位置如图所示．
当点F与点A重合时，记点G的位置为G″．
∴点G的运动轨迹为线段GG″．
过点C作CG′⊥BD于点G′．
∴|CG|min＝CG′＝BD．
∵正方形ABCD的边长为2，
∴BD＝2．
∴|CG|min＝．
故答案是：．
11．如图，菱形ABCD的边长为4，∠B＝120°，E是BC的中点，F是对角线AC上的动点，连接EF，将线段EF绕点F按逆时针旋转30°，G为点E对应点，连接CG，则CG的最小值为 ．
【答案】
【解答】解：如图取CD的中点K，连接FK，KG，EK，延长KG交BC于J，作CH⊥JK于H．
∵四边形ABCD是菱形，
∴∠FCE＝∠FCK，CB＝CD，AB∥CD，
∴∠DCB+∠B＝180°，
∵∠B＝120°，
∴∠DCB＝60°，
∵BE＝EC，CK＝KD，
∴CK＝CE，
∴△ECK是等边三角形，
∵CF＝CF，∠FCK＝∠FCE，CK＝CE，
∴△FCK≌△FCE（SAS），
∴FK＝FE，
∵FG＝FE，
∴FE＝FG＝FK，
∴∠EKG＝∠EFG＝15°，
∵∠CKE＝60°，
∴∠CKJ＝45°，
∴点G在直线KJ上运动，
根据垂线段最短可知，当点G与H重合时，CG的值最小，
在Rt△CKH中，∵∠CKH＝45°，∠CHK＝90°，CK＝CD＝2，
∴CH＝KH＝，
∴CG的最小值为，
故答案为．
12．已知边长为6的等边△ABC中，E是高AD所在直线上的一个动点，连接BE，将线段BE绕点B顺时针旋转60°得到BF，连接DF，则在点E运动的过程中，当线段DF长度的最小值时，DE的长度为 ．
【答案】
【解答】解：连接CF，
∵等边△ABC，
∴AB＝BC，
∵线段BE绕点B顺时针旋转60°得到BF，
∴BE＝BF，∠ABE＝∠CBF，
∴△ABE≌△BCF（ASA），
F点在直线CF上运动，
∴CF＝AE，∠BCF＝30°，
∴F点在直线CF上运动，
当DF⊥CF时，DF最小，
∵CD＝3，
∴CF＝，
∴AE＝，
∵AD＝3，
∴DE＝，
故答案为．
13．如图，线段AB＝2，点C为平面上一动点，且∠ACB＝90°，将线段AC的中点P绕点A顺时针旋转90°得到线段AQ，连接BQ，则线段BQ的最大值为 ．
【答案】
【解答】解：如图，取AB的中点D，连接CD，过点A作AE⊥AB，使AE＝AD＝，连接QE、BE．
∵∠ACB＝90°，D为AB的中点，
∴，
∵∠QAC＝90°，∠EAB＝90°，
∴∠QAE＝∠CAD，
∵，，
∴△ADC∽△AEQ，
∴，
∴，
∵∠EAB＝90°，
∴＝，
当点Q、E、B三点共线时，BQ最大为＝．
故答案为：．
14．如图，线段AB为⊙O的直径，点C在AB的延长线上，AB＝4，BC＝2，点P是⊙O上一动点，连接CP，以CP为斜边在PC的上方作Rt△PCD，且使∠DCP＝60°，连接OD，则OD长的最大值为 ．
【答案】2+1
【解答】解：如图，作△COE，使得∠CEO＝90°，∠ECO＝60°，则CO＝2CE，OE＝2，∠OCP＝∠ECD，
∵∠CDP＝90°，∠DCP＝60°，
∴CP＝2CD，
∴＝＝2，
∴△COP∽△CED，
∴＝＝2，
即ED＝OP＝1（定长），
∵点E是定点，DE是定长，
∴点D在半径为1的⊙E上，
∵OD≤OE+DE＝2+1，
∴OD的最大值为2+1，
故答案为．
14．已知⊙O的半径长7cm，P为线段OA的中点，若点P在⊙O上，则OA的长是 cm．
【答案】14
【解答】解：根据点和圆的位置关系，得OP＝7cm，
再根据线段的中点的概念，得OA＝2OP＝14cm．
故答案为：14．
15．如图，在△ABC中，AC：BC：AB＝3：4：5，⊙O沿着△ABC的内部边缘滚动一圈，若⊙O的半径为1，且圆心O运动的路径长为18，则△ABC的周长为 ．
【答案】30
【解答】解：设⊙O沿着△ABC的内部边缘滚动一圈，如图所示，
连接DE、EF、DF，
设切点分别为G、H、P、Q、M、N，
连接DH、DG、EP、EQ、FM、FN，
得矩形DEPG、矩形EQNF、矩形DEMH，
∴DE＝GP，EF＝QN，DF＝HM，
根据切线长定理四边形CPEQ是正方形，
∴PC＝PE＝EQ＝CQ＝1，
∵⊙O的半径为1，且圆心O运动的路径长为18，
∴DE+EF+DF＝18，
∵DE∥AC，DF∥AB，EF∥BC，
∴∠DEF＝∠ACB，∠DFE＝∠ABC，
∴△DEF∽△ABC，
∴DE：EF：DF＝AC：BC：AB＝3：4：5，
设DE＝3k（k＞0），则EF＝4k，DF＝5k，
∵DE+EF+DF＝18，
∴3k+4k+5k＝18，
解得k＝，
∴DE＝3k＝，EF＝4k＝6，DF＝5k＝，
根据切线长定理，
设AG＝AH＝x，BN＝BM＝y，
则AC＝AG+GP+CP＝x++1＝x+5.5，
BC＝CQ+QN+BN＝1+6+y＝y+7，
AB＝AH+HM+BM＝x++y＝x+y+7.5，
∵AC：BC：AB＝3：4：5，
∴（x+5.5）：（y+7）：（x+y+7.5）＝3：4：5，
解得x＝2，y＝3，
∴AC＝7.5，BC＝10，AB＝12.5，
∴AC+BC+AB＝30．
所以△ABC的周长为30．
故答案为30．
16．如图，⊙O的半径为2，O到定点A的距离为5，点B在⊙O上，点P是线段AB的中点，若B在⊙O上运动一周．
（1）点P的运动路径是一个圆；
（2）△ABC始终是一个等边三角形，直接写出PC长的取值范围．
【解答】（1）解：连接OA、OB，取OA的中点H，连接HP，如图1所示：
则HP是△ABO的中位线，
∴HP＝OB＝1，
∴P点到H点的距离固定为1，
∴B在⊙O上运动一周，点P运动的路径是以点H为圆心，半径为1的一个圆；
（2）解：连接AO并延长AO交⊙O于点M、N，如图2所示：
∵△ABC是等边三角形，点P是线段AB的中点，
∴PC⊥AB，PA＝PB＝AB＝BC，
∴PC＝PA＝AB，
当点B运动到点M位置时，点P运动到点P'位置，PC最短，
∵AM＝OA﹣OM＝5﹣2＝3，
∴AP'＝AM＝，
∴PC＝；
当点B运动到点N位置时，点P运动到点P''位置，PC最长，
∵AN＝OA+ON＝5+2＝7，
∴AP''＝AN＝，
∴PC＝；
∴PC长的取值范围是≤PC≤．
17．若AC＝4，以点C为圆心，2为半径作圆，点P为该圆上的动点，连接AP．
（1）如图1，取点B，使△ABC为等腰直角三角形，∠BAC＝90°，将点P绕点A顺时针旋转90°得到AP′．
①点P'的轨迹是 （填“线段”或者“圆”）；
②CP′的最小值是 ；
（2）如图2，以AP为边作等边△APQ（点A、P、Q按照顺时针方向排列），在点P运动过程中，求CQ的最大值．
（3）如图3，将点A绕点P逆时针旋转90°，得到点M，连接PM，则CM的最小值为 ．
【解答】解：（1）①连接CP、BP'，如图1所示：
∵△ABC是等腰直角三角形，∠BAC＝90°，
∴AC＝AB，由旋转的性质得：AP＝AP'，∠PAP'＝90°，
∴∠PAC＝∠P'AB，
在△ABP'和△ACP中，，
∴△ABP'≌△ACP（SAS），
∴BP'＝CP＝2，即点P'到点B的距离等于定长，
∴点P'的轨迹是以B为圆心，2为半径的圆；
故答案为：圆；
②∵△ABC是等腰直角三角形，AC＝4，
∴BC＝AC＝4，
当点P'在线段BC上时，CP'最小＝BC﹣BP'＝4﹣2；
故答案为：4﹣2；
（2）以AC为边长作等边△ACD，连接DQ、CP，如图2所示：
∵△APQ和△ACD是等边三角形，
∴AP＝AQ，AC＝AD＝CD＝4，∠PAQ＝∠CAD＝60°，
∴∠DAQ＝∠CAP，
在△ADQ和△ACP中，，
∴△ADQ≌△ACP（SAS），
∴DQ＝CP＝2，
当C、D、Q三点共线时，CQ有最大值＝CD+DQ＝4+2＝6；
（3）如图3所示：M点的轨迹是以MM'为直径的一个圆O'，
则PM＝PA＝2，PM'＝PA＝4+2＝6，
则CO'是梯形PMM'P'的中位线，
∴CO'＝（2+6）＝4，
连接MM'''，
则∠MM'''M'＝90°，
∴P'M'''＝PM＝2，MM'''＝PP'＝4，
∴M'M'''＝6﹣2＝4＝MM'''，
∴△MM'M'''是等腰直角三角形，∴MM'＝
MM'''＝4，
∴O'M''＝2，
∴CM＝CO'﹣O'M''＝4﹣2；
故答案为：4﹣2．
18．已知：如图，AB是⊙O的直径，C是⊙O上一点，OD⊥AC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接AE．
（1）求证：AE与⊙O相切；
（2）连接BD，若ED：DO＝3：1，OA＝9，求AE的长；
（3）若AB＝10，AC＝8，点F是⊙O任意一点，点M是弦AF的中点，当点F在⊙O上运动一周，则点M运动的路径长为 ．
【解答】（1）证明：如图1中，连接OC．
∵OD⊥AC，
∴AD＝DC，
∴EA＝EC，
在△OEC和△OEA中，
，
∴△OEC≌△OEA，
∴∠OAE＝∠OCE，
∵EC是⊙O切线，
∴EC⊥OC，
∴∠OCE＝90°，
∴∠OAE＝∠OCE＝90°，
∴OA⊥AE，
∴AE是⊙O的切线．
（2）如图1中，设OD＝a，则DE＝3a，
∵∠AOD＝∠AOE，∠ODA＝∠OAE，
∴△OAD∽△OEA，
∴＝，
∴4a2＝81，
∵a＞0，
∴a＝，
∴OE＝18，
在Rt△AOE中，AE＝＝＝9．
（3）如图2中，连接OM，取OA的中点O′，连接O′M．
∵AM＝MF，
∴OM⊥AF，
∵AO′＝OO′，OA＝OB＝5，
∴O′M＝OA＝定长＝，
∴当点F在⊙O上运动一周，则点M运动的路径是以O′为圆心为半径的圆，
∴点M运动的路径长为2π•＝5π．
故答案为5π．
19．如图1，在平面直角坐标系中，直线y＝﹣5x+5与x轴，y轴分别交于A、C两点，抛物线y＝x2+bx+c经过A、C两点，与x轴的另一交点为B．
（1）求抛物线解析式；
（2）若点M为x轴下方抛物线上一动点，当点M运动到某一位置时，△ABM的面积等于△ABC面积的，求此时点M的坐标；
（3）如图2，以B为圆心，2为半径的⊙B与x轴交于E、F两点（F在E右侧），若P点是⊙B上一动点，连接PA，以PA为腰作等腰Rt△PAD，使∠PAD＝90°（P、A、D三点为逆时针顺序），连接FD．求FD长度的取值范围．
【解答】解：（1）令x＝0，则y＝5，
∴C（0，5），
令y＝0，则x＝1，
∴A（1，0），
将点A（1，0），C（0，5）代入y＝x2+bx+c，
得，
∴，
∴y＝x2﹣6x+5；
（2）设M（m，m2﹣6m+5），
令y＝0，则x2﹣6x+5＝0，
解得x＝5或x＝1，
∴B（5，0），
∴AB＝4，
∴S△ABC＝×4×5＝10，
∵△ABM的面积等于△ABC面积的，
∴S△AMB＝6＝×4×（m2﹣6m+5），
解得m＝2或m＝4，
∴M（2，﹣3）或M（4，﹣3）；
（3）将点B绕A点顺时针旋转90°到B'，连接AB'，PB，B'D，
∵∠B'AD+∠BAD＝90°，∠PAB+∠BAD＝90°，
∴∠B'AD＝∠PAB，
∵AB＝AB'，PA＝AD，
∴△ADB'≌△APB'（SAS），
∴BP＝B'D，
∵PB＝2，
∴B'D＝2，
∴D在以B'为圆心，2为半径的圆上运动，
∵B（5，0），A（1，0），
∴B'（1，﹣4），
∵BF＝2，
∴F（7，0），
∴B'F＝2，
∴DF的最大值为2+2，DF的最小值为2﹣2，
∴2﹣2≤DF≤2+2．
（1）思路引导
要证点P运动的路径是一个圆，只要证点P到定点M的距离等于定长r，由图中的定点、定长
可以发现M，r．