资料中包含下列文件,点击文件名可预览资料内容




还剩28页未读,
继续阅读
成套系列资料,整套一键下载
第7章《平面图形的认识(二)》-2023-2024学年数学七年级下册章节复习讲讲义(苏科版)
展开
这是一份第7章《平面图形的认识(二)》-2023-2024学年数学七年级下册章节复习讲讲义(苏科版),文件包含第7章平面图形的认识二教师版docx、第7章平面图形的认识二学生版docx等2份学案配套教学资源,其中学案共44页, 欢迎下载使用。
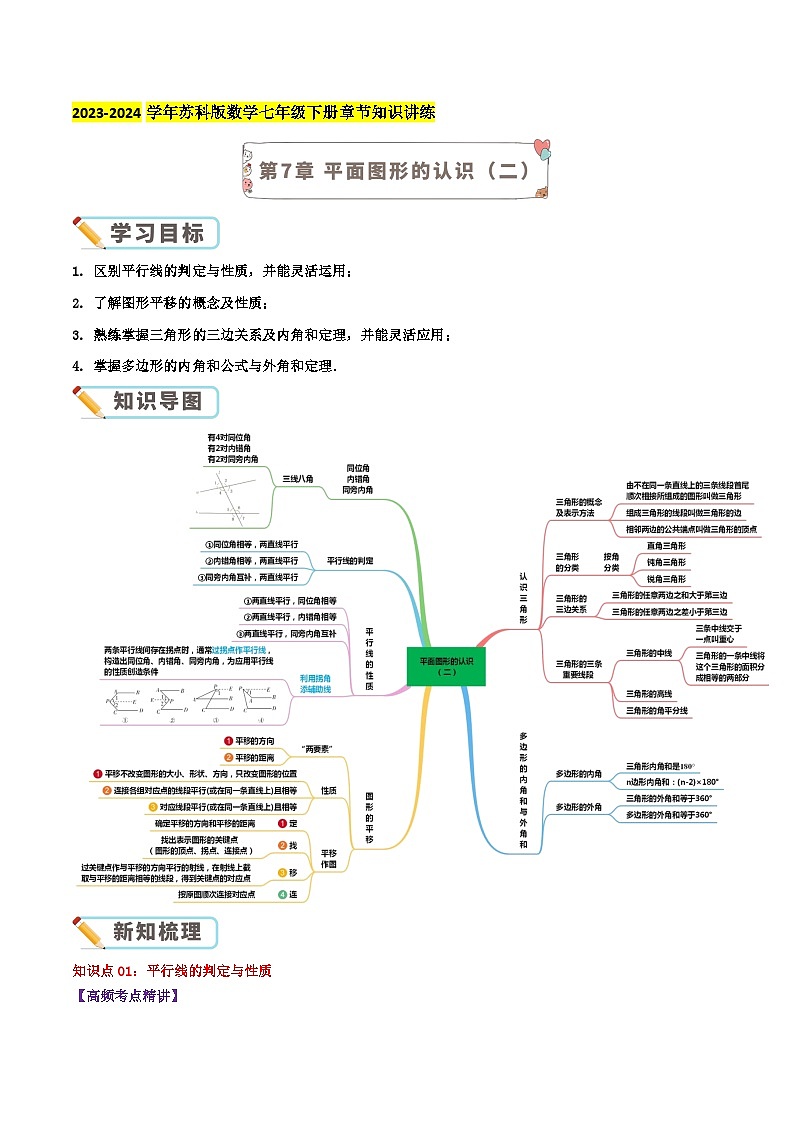
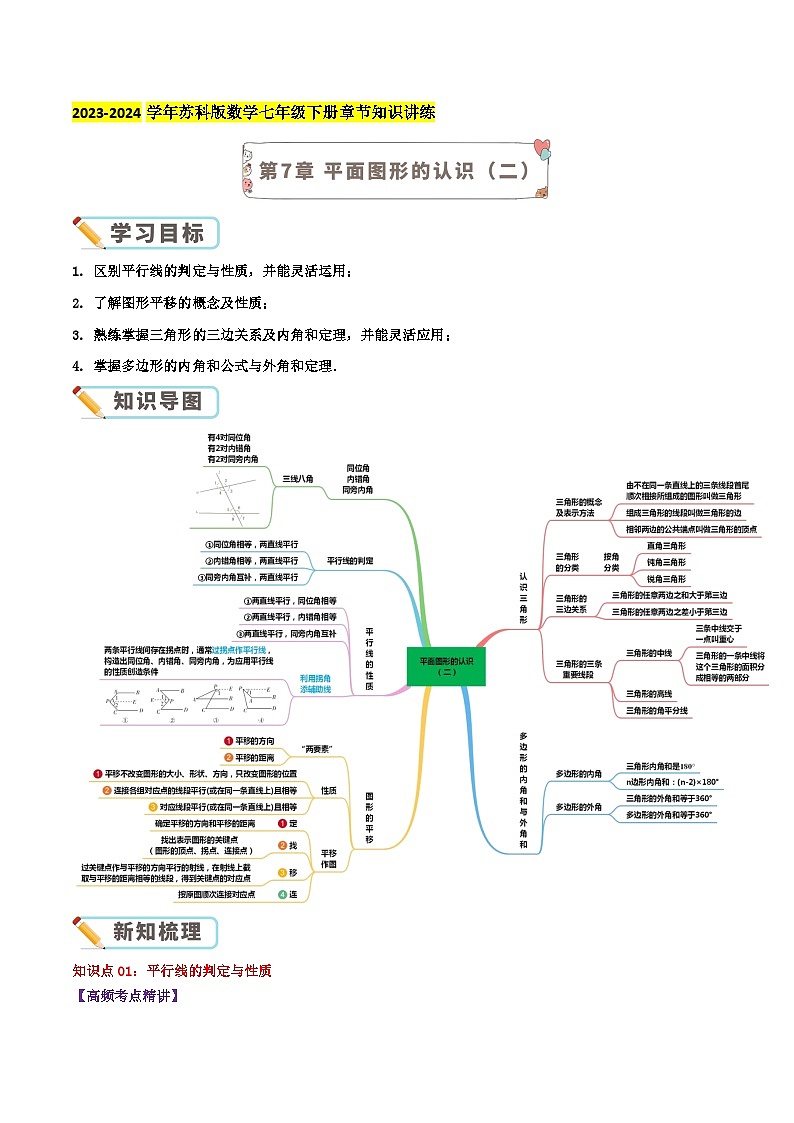
2023-2024学年苏科版数学七年级下册章节知识讲练1. 区别平行线的判定与性质,并能灵活运用;2. 了解图形平移的概念及性质;3. 熟练掌握三角形的三边关系及内角和定理,并能灵活应用;4. 掌握多边形的内角和公式与外角和定理.知识点01:平行线的判定与性质【高频考点精讲】 1.平行线的判定判定方法1:同位角相等,两直线平行.判定方法2:内错角相等,两直线平行.判定方法3:同旁内角互补,两直线平行.【易错点剖析】根据平行线的定义和平行公理的推论,平行线的判定方法还有:(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行.(2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性).(3)在同一平面内,垂直于同一直线的两条直线平行.(4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.2.平行线的性质性质1:两直线平行,同位角相等;性质2:两直线平行,内错角相等;性质3:两直线平行,同旁内角互补.【易错点剖析】根据平行线的定义和平行公理的推论,平行线的性质还有:(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.知识点02:图形的平移【高频考点精讲】 1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移.【易错点剖析】决定平移的两个要素:(1)平移的方向;(2)平移的距离.2.平移的性质: (1)图形的平移不改变图形的形状与大小,只改变图形的位置.(2)图形平移后,对应点的连线平行或在同一直线上且相等. (3)图形经过平移,对应线段互相平行或在同一条直线上且相等,对应角相等.知识点03:认识三角形【高频考点精讲】 三角形的分类 (1)按角分: 三角形2.三角形的三边关系三角形的任意两边之和大于第三边; 三角形任意两边之差小于第三边.【易错点剖析】(1)判断给定三条线段能否构成一个三角形:看较小两边的和是否大于最长边.(2)已知三角形的两边长,确定第三边的范围:两边之差的绝对值<第三边<两边之和.3.三角形的三条主要线段(1)在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。三角形的三条中线交于三角形内部一点,叫做三角形的重心.(2)在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线,三角形的三条角平分线交于三角形内一点,叫做三角形的内心.(3)在三角形中,从一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高,三角形的三条高交于一点,叫做三角形的垂心.4.三角形的角(1)三角形的内角和为180°.(2) 三角形的一边与他的邻边的延长线组成的角叫做三角形的外角.【易错点剖析】(1)直角三角形的两个锐角互余;(2)三角形的一个外角等于与它不相邻的两内角和;(3)三角形的一个外角大于任意一个不相邻的内角.知识点04:多边形的内角和与外角和【高频考点精讲】 1. 多边形的内角和:边形的内角和为(-2)·180°(≥3).【易错点剖析】(1)内角和定理的应用:①已知多边形的边数,求其内角和;②已知多边形内角和求其边数; (2)正多边形的每个内角都相等,都等于. 2. 多边形的外角和:任意多边形的外角和都为360°.【易错点剖析】多边形的外角和为360°.边形的外角和恒等于360°,它与边数的多少无关.检测时间:120分钟 试题满分:100分 难度系数:0.55一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2024•邵阳模拟)如图,直线l1∥l2,分别与直线l交于点A,B,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=50°,则∠2的度数是( )A.130° B.100° C.90° D.70°解:如图,∵直线l1∥l2,∴∠1=∠3,∵∠1=50°,∴∠3=50°,由题意知∠4=30°,∴∠2=180°﹣∠3﹣∠4=180°﹣50°﹣30°=100°,故选:B.2.(2分)(2023秋•成华区期末)如图,直线AB∥CD,∠ABE=45°,∠E=20°,则∠D的度数为( )A.20° B.25° C.30° D.35°解:∵AB∥CD,∴∠ABE=∠BCD=45°,∴∠DCE=135°,由三角形的内角和可得∠D=180°﹣135°﹣20°=25°.故选:B.3.(2分)(2023秋•东城区期末)一个多边形的内角和等于外角和的两倍,那么这个多边形是( )A.三边形 B.四边形 C.五边形 D.六边形解:设这个多边形的边数为n,由题意得:(n﹣2)•180°=360°×2,n﹣2=4,n=6,故选:D.4.(2分)(2023秋•东莞市校级期末)为估计池塘两岸A、B间的距离,晓聪在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离可能是( )A.2m B.30m C.28m D.20m解:根据三角形的三边关系定理可得:16﹣12<AB<16+12,即4<AB<28,故选:D.5.(2分)(2023秋•桐乡市期末)如图,为了估计池塘两岸A,B间的距离,在池塘的一侧选取点P,测得PA=14 米,PB=9米,那么A,B间的距离不可能是( )A.6米 B.8.7米 C.27米 D.18米解:由三角形三边关系定理得:14﹣9<AB<14+9,5<AB<23,∴A,B间的距离不可能是27米.故选:C.6.(2分)(2023秋•射洪市期末)如图,下列条件中不能判定AB∥CD的是( )A.∠1=∠2 B.∠3=∠4 C.∠3+∠5=180° D.∠2=∠3解:A、∵∠1=∠2,∴∠3=∠5,因为”同旁内角互补,两直线平行“,所以本选项不能判断AB∥CD,符合题意;B、∵∠3=∠4,∴AB∥CD,故本选项能判定AB∥CD,不符合题意;C、∵∠3+∠5=180°,∴AB∥CD,故本选项能判定AB∥CD,不符合题意;D、∵∠1=∠5,∴AB∥CD,故本选项能判定AB∥CD,不符合题意.故选:A.7.(2分)(2023秋•太康县期末)如图,点E在CD延长线上,下列条件中不能判定AC∥BD的是( )A.∠1=∠2 B.∠3=∠4 C.∠5=∠C D.∠C+∠BDC=180°解:A.∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,所以A选项不符合题意.B.∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),不能判定BD∥AC,所以B选项符合题意.C.∵∠5=∠C,∴BD∥AC (同位角相等,两直线平行),所以C选项不合题意.D.∵∠C+∠BDC=180°,∴BD∥AC(同旁内角互补,两直线平行),所以D选项不合题意.故选:B.8.(2分)(2023秋•钟祥市校级期中)如图,∠AOB=70°,点M,N分别在OA,OB上运动(不与点O重合),ME平分∠AMN,ME的反向延长线与∠MNO的平分线交于点F,在M,N的运动过程中,∠F的度数( )A.变大 B.变小 C.等于55° D.等于35°解:∵ME平分∠AMN,NF平分∠MNO,∴∠EMN=∠AMN,∠MNF=∠MNO,根据外角的定义:∠AMN=∠AOB+∠MNO,∴∠EMN=∠AOB+∠MNO,∵∠AOB=70°,∴∠EMN=×70°+∠MNF=35°+∠MNF,根据外角的定义:∠EMN=∠F+∠MNF,∴∠F=35°,故选:D.9.(2分)(2023春•鼓楼区校级期末)如图,在△ABC,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC﹣∠C);④∠BGH=∠ABE+∠C,正确的是( )A.1 B.2 C.3 D.4解:设BD交FH于点J.①∵BD⊥FD,∴∠FJD+∠F=90°∵FH⊥BE,∴∠BJG+∠DBE=90°,∵∠FJD=∠BJG,∴∠DBE=∠F,①正确;②∵BE平分∠ABC,∴∠ABE=∠CBE,∠BEF=∠CBE+∠C,∴2∠BEF=∠ABC+2∠C,∠BAF=∠ABC+∠C,∴2∠BEF=∠BAF+∠C,②正确;③∠ABD=90°﹣∠BAC,∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,∵∠CBD=90°﹣∠C,∴∠DBE=∠BAC﹣∠C﹣∠DBE,由①得,∠DBE=∠F,∴∠F=∠BAC﹣∠C﹣∠DBE,∴∠F=(∠BAC﹣∠C);③正确;④∵∠AEB=∠EBC+∠C,∵∠ABE=∠CBE,∴∠AEB=∠ABE+∠C,∵BD⊥FC,FH⊥BE,∴∠FGD=∠FEB,∴∠BGH=∠ABE+∠C,④正确,故选:D.10.(2分)(2023秋•兰州期末)如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥EH于点G,且∠AFG=2∠D,则下列结论:①∠D=40°;②2∠D+∠EHC=90°;③FD平分∠HFB;④FH平分∠GFD.其中正确结论的个数是( )A.1个 B.2个 C.3个 D.4个解:延长FG,交CH于I.∵AB∥CD,∴∠BFD=∠D,∠AFI=∠FIH,∵FD∥EH,∴∠EHC=∠D,∵FE平分∠AFG,∴∠FIH=2∠AFE=2∠EHC,∴3∠EHC=90°,∴∠EHC=30°,∴∠D=30°,∴2∠D+∠EHC=2×30°+30°=90°,∴①∠D=40°错误;②2∠D+∠EHC=90°正确,∵FE平分∠AFG,∴∠AFI=30°×2=60°,∵∠BFD=30°,∴∠GFD=90°,∴∠GFH+∠HFD=90°,可见,∠HFD的值未必为30°,∠GFH未必为45°,只要和为90°即可,∴③FD平分∠HFB,④FH平分∠GFD不一定正确.故选:A.二.填空题(共10小题,满分20分,每小题2分)11.(2分)(2023秋•旌阳区期末)如图,在△ABC中,AD平分∠BAC交BC于点D,CE⊥AB于点E,若∠B=50°,∠ACE=20°,则∠ADC的度数是 85° .解:∵∠B=50°,CE⊥AB,∴∠BCE=90°﹣∠B=40°,∴∠ACB=∠BCE+∠ACE=40°+20°=60°,∴∠BAC=180°﹣∠B﹣∠ACB=70°.∵AD平分∠BAC,∴.∴∠ADC=180°﹣∠DAC﹣∠ACB=85°.故答案为:85°.12.(2分)(2023秋•鹰潭期末)如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.若∠A=30°,∠BDC=50°,则∠BDE的度数是 20° .解:∵∠A=30°,∠BDC=50°,∴∠ABD=∠BDC﹣∠A=20°.∵BD是△ABC的角平分线,∴∠DBC=∠ABD=20°,∵DE∥BC,∴∠BDE=∠DBC=20°.故答案为:20°.13.(2分)(2023秋•汉中期末)如图,BE,CF是△ABC的角平分线,∠ABC=60°,∠ACB=80°,BE,CF相交于点D,则∠CDE的度数是 70° .解:∵BE,CF是△ABC的角平分线,∠ABC=60°,∠ACB=80°,∴,,∴∠EDC=∠DBC+∠DCB=70°.故答案为:70°.14.(2分)(2023秋•石嘴山校级期中)如图,在五边形ABCDE中,∠A+∠B+∠E=310°,DP,CP分别平分∠EDC,∠BCD,则∠CPD的度数是 65° .解:∵五边形的内角和等于540°,∠A+∠B+∠E=310°,∴∠BCD+∠CDE=540°﹣310°=230°,∵∠BCD、∠CDE的平分线在五边形内相交于点P,∴∠PDC+∠PCD=(∠BCD+∠CDE)=115°,∴∠CPD=180°﹣115°=65°.故答案为:65°.15.(2分)(2023秋•钟祥市校级期中)一张△ABC纸片,点M、N分别是AB、AC上的点,若沿直线MN折叠后,点A落在AC边的下面A′的位置,如图所示,则∠1,∠2,∠A之间的数量关系式是 ∠1=2∠A+∠2 .解:如图,由折叠得:∠A=∠A′,∵∠1是△MDA的外角,∴∠1=∠A+∠MDA,同理:∠MDA=∠2+∠A′,∴∠1=∠A+∠2+∠A′,即:∠1=2∠A+∠2,故答案为:∠1=2∠A+∠2.16.(2分)(2023秋•湛江期末)如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是 80° .解:∵∠CAB的外角=∠B+∠C,且∠CAB的外角等于120°,∠B等于40°,∴∠C=80°,故答案为:80°.17.(2分)(2023秋•丹东期末)如图,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,∠D=15°,则∠A= 30° .解:∵∠ABC的平分线与∠ACE的平分线交于点D,∴∠ABD=∠CBD,∠ACD=∠ECD,∵∠ACE=∠A+∠ABC,即∠ACD+∠ECD=∠ABC+∠CBD+∠A,∴2∠ECD=2∠CBD+∠A,∴∠A=2(∠ECD﹣∠CBD)∵∠ECD=∠CBD+∠D,∠D=15°∴∠D=∠ECD﹣∠CBD=15°∴∠A=2×15°=30°.故答案为:30°.18.(2分)(2023秋•吉林期末)如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是 190° .解:如图,(9﹣2)×180°÷9×2=7×180°÷9×2=280°,∠3+∠4=180°﹣90°=90°,∠1+∠2=280°﹣90°=190°.故答案为:190°.19.(2分)(2022秋•济阳区期末)如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,以每秒2cm的速度沿A→C→E运动.若设点P运动的时间是t s,那么当t= 2或 s时,△APE的面积等于8.解:∵BC=8cm,点E是BC的中点,∴CE=BC=4cm,当点P在线段AC上,如图1所示,AP=2t,∵∠C=90°,∴S△APE=AP•CE=×2t×4=4t=8,解得:t=2;当点P在线段CE上,如图2所示,AC=6cm,PE=10﹣2t,∴S△APE=PE•AC=×(10﹣2t)×6=8,解得:t=.故答案为:2或.20.(2分)(2023春•慈溪市期中)如图,PQ∥MN,A,B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣4|+(b﹣1)2=0.若射线AM绕点A顺时针先转动18秒,射线BQ才开始绕点B逆时针旋转,在射线BQ到达BA之前,问射线AM再转动 或36 秒时,射线AM与射线BQ互相平行.解:∵|a−4|+(b−1)2=0,∴a=4,b=1,设射线AM再转动t秒时,射线AM、射线BQ互相平行.如图,射线AM绕点A顺时针先转动18秒后,AM转动至AM'的位置,∠MAM'=18×4=72°,分两种情况:①当M″到达MN前,∠QBQ'=t°,∠M'AM″=4t°,∵∠BAN=45°=∠ABQ,∴∠MAB=135°,∴∠M'AB=135°﹣72°=63°,∴∠ABQ'=45°﹣t°,∠BAM″=∠M'AM″﹣∠M'AB=4t°﹣63°,当∠ABQ'=∠BAM″时,BQ'∥AM″,此时,45°﹣t°=4t°﹣63°,解得t=;②当M″到达MN后,∠QBQ'=t°,∠NAM″=4t°﹣(180﹣72)°=4t°﹣108°,∠BAM″=45°﹣(4t°﹣108°)=153°﹣4t°,∵∠BAN=45°=∠ABQ,∴∠ABQ'=45°﹣t°,,当∠ABQ'=∠BAM″时,BQ'∥AM″,此时,45°﹣t°=153°﹣4t°,解得t=36;综上所述,射线AM再转动或36秒时,射线AM、射线BQ互相平行.故答案为:或36.三.解答题(共8小题,满分60分)21.(6分)(2023秋•德化县期末)如图,若∠DAE=∠E,∠B=∠D,那么AB∥DC吗?请在下面的解答过程中填空或在括号内填写理由.解:理由如下:∵∠DAE=∠E(已知),∴ AD ∥ BE ( 内错角相等,两直线平行 ),∴∠DCE= ∠D ( 两直线平行,内错角相等 ),又∵∠B=∠D(已知),∴∠DCE= ∠B ( 等量代换 ),∴AB∥DC( 同位角相等,两直线平行 ).解:∵∠DAE=∠E(已知),∴AD∥BE(内错角相等,两直线平行),∴∠DCE=∠D(两直线平行,内错角相等),又∵∠B=∠D(已知),∴∠DCE=∠B(等量代换),∴AB∥DC(同位角相等,两直线平行),故答案为:AD;BE;内错角相等,两直线平行;∠D;两直线平行,内错角相等;∠B;等量代换;同位角相等,两直线平行.22.(6分)(2023秋•商河县期末)如图,在△ABC中,∠AGF=∠ABC,∠1+∠2=180°.(1)求证:DE∥BF;(2)若DE⊥AC,∠2=140°,求∠AFG的度数.解:(1)BF∥DE,理由如下:∵∠AGF=∠ABC,∴GF∥BC,∴∠1=∠CBF,∵∠1+∠2=180°,∴∠CBF+∠2=180°,∴BF∥DE;(2)∵BF∥DE,DE⊥AC,∴BF⊥AC,∵∠1+∠2=180°,∠2=140°,∴∠1=40°,∴∠AFG=90°﹣40°=50°.23.(8分)(2023秋•凤翔区期末)如图,将一副三角板中的两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°.【观察猜想】(1)∠BCD与∠ACE的数量关系是 ∠BCD=∠ACE ;∠BCE与∠ACD的数量关系是 ∠BCE+∠ACD=180° ;【类比探究】(2)若保持三角板ABC不动,绕直角顶点C顺时针转动三角板DCE,试探究当∠ACD等于多少度时CE∥AB,画出图形并简要说明理由;【拓展应用】(3)若∠BCE=3∠ACD,求∠ACD的度数;并直接写出此时DE与AC的位置关系.解:(1)∵∠BCD+∠ACD=90°,∠ACE+∠ACD=90°,∴∠BCD=∠ACE;∵∠BCE=∠ACB+∠ACE=90°+∠ACE,∴∠BCE+∠ACD=90°+∠ACE+∠ACD=90°+90°=180°,∴∠BCE+∠ACD=180°.故答案为:∠BCD=∠ACE;∠BCE+∠ACD=180°;(2)分两种情况:①如图1所示,当CE∥AB时,∠ACE=∠A=30°,∴∠ACD=∠DCE﹣∠ACE=90°﹣30°=60°.②如图2所示,当CE∥AB时,∠BCE=∠B=60°,∴∠ACD=360°﹣∠ACB﹣∠BCE﹣∠DCE=360°﹣90°﹣60°﹣90°=120°.综上所述,当∠ACD等于60°或120°时,CE∥AB;(3)设∠ACD=α,则∠BCE=3α.由(1)可知,∠BCE+∠ACD=180°,∴3α+α=180°,∴α=45°,即∠ACD=45°,此时DE⊥AC或DE∥AC.24.(8分)(2023秋•鹰潭期末)生活现象如图1,杆秤是中国最古老也是现今人们仍然在使用的衡量工具,是利用杠杆原理来称质量的简易衡器,由木制的带有秤星的秤杆、金属秤砣、提绳等组成.数学模型如图2,是杆秤的示意图,AC∥BD,经测量发现∠A=104°,∠BOE=76°,请判断OE与BD的位置关系,并说明理由.解:OE∥BD,理由如下:∵AC∥BD,∴∠A+∠ABD=180°,∴∠ABD=180°﹣104°=76°,∴∠ABD=∠BOE,∴OE∥BD.25.(8分)(2023秋•城阳区期末)【发现问题】如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.【提出问题】小明提出:∠BPD,∠ABP和∠CDP三个角之间存在着怎样的数量关系?【分析问题】已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.【解决问题】探究一:请你帮小明解决这个问题,并说明理由.探究二:如图②,∠P,∠AMP,∠CNP的数量关系为 ∠BPD=∠ABP+∠CDP ;如图③,已知∠ABC=25°,∠C=60°,AE∥CD,则∠BAE= 145 °(不需要写解答过程)利用探究一得到的结论解决下列问题:如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P=2∠F,求∠FME的度数.解:探究一:∠BPD=∠ABP+∠CDP,理由如下:如图①,∵AB∥MN∥CD,∴∠BPN=∠ABP,∠DPN=∠CDP,∴∠BPN+∠DPN=∠ABP+∠CDP,∴∠BPD=∠ABP+∠CDP.探究二:如图②,∠AMP=∠P+∠CNP,理由如下:∵AB∥CD,∴∠MKP=∠CNP,∵∠AMP=∠P+∠MKP,∴∠AMP=∠P+∠CNP.如图③,延长EA交BC于L,∵AE∥CD,∴∠ALC=∠C=60°,∴∠ALB=180°﹣∠ALC=120°,∴∠BAE=∠B+∠ALB=25°+120°=145°.故答案为:∠AMP=∠P+∠CNP,145.∵射线ME,NF分别平分∠BMP和∠CNP,∴∠PME=∠PMB,∠CNF=∠PNF,如图④,由探究一的结论得:∠P=∠AMF+∠PMF+∠CNF+∠PNF,∠F=∠AMF+∠CNF,∵∠P=2∠F,∴∠AMF+∠PMF+∠CNF+∠PNF=2∠AMF+2∠CNF,∵∠CNF=∠PNF,∴∠AMF+∠PMF=2∠AMF,∴∠PMF=∠AMF=∠AMP,∴∠PMF+∠PME=(∠AMP+∠PMB),∴∠FME=∠AMB=×180°=90°.26.(8分)(2023秋•海口期末)将一副直角三角尺的直角顶点C按照如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°),并能绕C点自由旋转.(1)写出∠ACB与∠DCE的数量关系,并说明理由;(2)当0°<∠ACE<180°且点E在直线AC的上方时,固定直角三角尺ACD,将直角三角尺ECB绕C点自由旋转.①当EB∥AC时,∠ACE= 45°或135° °;②要使CB∥AD,则∠ACE的度数为 30°或150° °,请说明理由;③直接写出分别使得CE∥AD,EB∥DC,EB∥AD的∠ACE的度数,在备用图中画出相应的草图,不必写出理由.解:(1)∠ACB与∠DCE的数量关系是:∠ACB+∠DCE=180°,理由如下:∵∠A=60°,∠D=30°,∠E=∠B=45°,∴∠ACD=90°,∠BCE=90°,∴∠ACB=∠ACD+∠DCB=90°+∠DCB,∠DCE=∠BCE﹣∠DCB=90°﹣∠DCB,∴∠ACB+∠DCE=90°+∠DCB+90°﹣∠DCB=180°;(2)①当EB∥AC时,有以下两种情况:(ⅰ)当BE在AC的上方时,如图1所示:∵EB∥AC,∠E=45°,∴∠ACE=∠E=45°,(ⅱ)当BE在AC下方时,如图2所示:∵EB∥AC,∠B=45°,∴∠ACB=∠B=45°,∴∠ACE=∠ACB+∠BCE=45°+90°=135°,综上所述:∠ACE=45°或135°,故答案为:45°或135°.②要使CB∥AD,则∠ACE的度数为60°或150°,理由如下:有以下两种情况:(ⅰ)当CB在AC的上方时,如图3所示:∵CB∥AD,∠D=30°,∴∠DCB=∠D=30°,∴∠DCE=∠BCE﹣∠DCB=90°﹣30°=60°,∴∠ACE=∠ACD﹣∠DCE=90°﹣60°=30°;(ⅱ)当CB在AC的下方时,如图4所示:∵CB∥AD,∠A=60°,∴∠ACB=∠A=60°,∴∠ACE=∠ACB+∠BCE=60°+90°=150°,综上所述:∠ACE的度数为30°或150°;故答案为:60°或150°.③当CE∥AD时,有以下两种情况:(ⅰ)当CE在AC上方时,如图5所示:∵CE∥AD,∠D=30°,∴∠DCE=∠D=30°,∴∠ACE=∠ACD+∠DCE=90°+30°=120°;(ⅱ)当CE在AC下方时,如图6所示:∵CE∥AD,∠A=60°,∴∠ACE=∠A=60°,综上所述:当CE∥AD时,∠ACE的度数为120°或60°;当EB∥DC时,有以下两种情况:(ⅰ)当BE在CD的左侧时,如图7所示:∵EB∥DC,∠B=45°,∴∠BCD=∠B=45°,∴∠ACB=∠ACD﹣∠BCD=90°﹣45°=45°,∴∠ACE=∠BCE﹣∠ACB=90°﹣45°=45°,(ⅱ)当BE在CD的右侧时,如图8所示:∵EB∥DC,∠E=45°,∴∠DCE=∠E=45°,∴∠ACE=∠ACD+∠DCE=90°+45°=135°,综上所述:当EB∥DC时,∠ACE的度数为45°或135°;当EB∥AD时,有以下两种情况:(ⅰ)当EB在AD的左侧时,如图9所示:设BC与AD交于点T,∵EB∥AD,∠B=45°,∴∠ATC=∠B=45°,∴∠ACT=180°﹣(∠ATC+∠A)=180°﹣(45°+60°)=75°,∴∠ACE=∠BCE﹣∠ACT=90°﹣75°=15°,(ⅱ)当EB在AD的右侧时,如图10所示:延长AC交EB于点H,∵EB∥AD,∠A=60°,∴∠CHE=180°﹣∠A=180°﹣60°=120°,∴∠ECH=180°﹣(CHE+∠E)=180°﹣(120°+45°)=15°,∵∠ACD=90°,∴∠DCH=90°,∴∠DCE=∠DCH﹣∠ECH=90°﹣15°=75°,∴∠ACE=∠ACD+∠DCE=90°+75°=165°,综上所述:当EB∥AD时,∠ACE的度数为15°或165°.∴当CE∥AD时,∠ACE的度数为120°或60°;当EB∥DC时,∠ACE的度数为45°或135°;当EB∥AD时,∠ACE的度数为15°或165°.27.(8分)(2023秋•大东区期末)如图,四边形BCED中,点A在CB的延长线上,点F在DE的延长线上,连接AF交BD于G,交CE于H,且∠1=45°,∠2=135°.(1)求证:BD∥CE;(2)若∠C=∠D,求证:∠A=∠F.证明:(1)∵∠CHG+∠2=180°,∠2=135°,∴∠CHG=45°,∵∠1=45°,∴∠CHG=∠1,∴BD∥CE.(2)∵BD∥CE,∴∠C=∠ABD,∵∠C=∠D,∴∠ABD=∠D.∴AC∥DF,∴∠A=∠F.28.(8分)(2023秋•潍城区期末)已知ABCD为四边形,点E为边AB延长线上一点.【探究】:(1)如图1,∠ADC=110°,∠BCD=120°,∠DAB和∠CBE的平分线交于点F,则∠AFB= 35 °;(2)如图2,∠ADC=α,∠BCD=β,且α+β>180°,∠DAB和∠CBE的平分线交于点F,则∠AFB= ;(用α,β表示)(3)如图3,∠ADC=α,∠BCD=β,当∠DAB和∠CBE的平分线AG,BH平行时,α,β应该满足怎样的数量关系?请证明你的结论;【挑战】:如果将(2)中的条件α+β>180°改为α+β<180°,再分别作∠DAB和∠CBE的平分线,若两平分线所在的直线交于点F,则∠AFB与α,β有怎样的数量关系?请画出图形并直接写出结论.解:(1)如图1.∵BF平分∠CBE,AF平分∠DAB,∴∠FBE=∠CBE,∠FAB=∠DAB.∵∠D+∠DCB+∠DAB+∠ABC=360°,∴∠DAB+∠ABC=360°﹣∠D﹣∠DCB=360°﹣120°﹣110°=130°.又∵∠F+∠FAB=∠FBE,∴∠F=∠FBE﹣∠FAB===(180°﹣130°)=25°;(2)如图2.由(1)得:∠AFB=,∠DAB+∠ABC=360°﹣∠D﹣∠DCB.∴∠AFB==.(3)若AG∥BH,则α+β=180°.证明:如图3.若AG∥BH,则∠GAB=∠HBE.∵AG平分∠DAB,BH平分∠CBE,∴∠DAB=2∠GAB,∠CBE=2∠HBE.∴∠DAB=∠CBE.∴AD∥BC.∴∠DAB+∠DCB=α+β=180°.挑战:如图4.∵AM平分∠DAB,BN平分∠CBE,∴∠BAM=,.∵∠D+∠DAB+∠ABC+∠BCD=360°,∴∠DAB+∠ABC=360°﹣∠D﹣BCD=360°﹣α﹣β.∴∠DAB+180°﹣∠CBE=360°﹣α﹣β.∴∠DAB﹣∠CBE=180°﹣α﹣β.∵∠ABF与∠NBE是对顶角,∴∠ABF=∠NBE.又∵∠F+∠ABF=∠MAB,∴∠F=∠MAB﹣∠ABF.∴∠F===90°﹣
2023-2024学年苏科版数学七年级下册章节知识讲练1. 区别平行线的判定与性质,并能灵活运用;2. 了解图形平移的概念及性质;3. 熟练掌握三角形的三边关系及内角和定理,并能灵活应用;4. 掌握多边形的内角和公式与外角和定理.知识点01:平行线的判定与性质【高频考点精讲】 1.平行线的判定判定方法1:同位角相等,两直线平行.判定方法2:内错角相等,两直线平行.判定方法3:同旁内角互补,两直线平行.【易错点剖析】根据平行线的定义和平行公理的推论,平行线的判定方法还有:(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行.(2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性).(3)在同一平面内,垂直于同一直线的两条直线平行.(4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.2.平行线的性质性质1:两直线平行,同位角相等;性质2:两直线平行,内错角相等;性质3:两直线平行,同旁内角互补.【易错点剖析】根据平行线的定义和平行公理的推论,平行线的性质还有:(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.知识点02:图形的平移【高频考点精讲】 1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移.【易错点剖析】决定平移的两个要素:(1)平移的方向;(2)平移的距离.2.平移的性质: (1)图形的平移不改变图形的形状与大小,只改变图形的位置.(2)图形平移后,对应点的连线平行或在同一直线上且相等. (3)图形经过平移,对应线段互相平行或在同一条直线上且相等,对应角相等.知识点03:认识三角形【高频考点精讲】 三角形的分类 (1)按角分: 三角形2.三角形的三边关系三角形的任意两边之和大于第三边; 三角形任意两边之差小于第三边.【易错点剖析】(1)判断给定三条线段能否构成一个三角形:看较小两边的和是否大于最长边.(2)已知三角形的两边长,确定第三边的范围:两边之差的绝对值<第三边<两边之和.3.三角形的三条主要线段(1)在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。三角形的三条中线交于三角形内部一点,叫做三角形的重心.(2)在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线,三角形的三条角平分线交于三角形内一点,叫做三角形的内心.(3)在三角形中,从一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高,三角形的三条高交于一点,叫做三角形的垂心.4.三角形的角(1)三角形的内角和为180°.(2) 三角形的一边与他的邻边的延长线组成的角叫做三角形的外角.【易错点剖析】(1)直角三角形的两个锐角互余;(2)三角形的一个外角等于与它不相邻的两内角和;(3)三角形的一个外角大于任意一个不相邻的内角.知识点04:多边形的内角和与外角和【高频考点精讲】 1. 多边形的内角和:边形的内角和为(-2)·180°(≥3).【易错点剖析】(1)内角和定理的应用:①已知多边形的边数,求其内角和;②已知多边形内角和求其边数; (2)正多边形的每个内角都相等,都等于. 2. 多边形的外角和:任意多边形的外角和都为360°.【易错点剖析】多边形的外角和为360°.边形的外角和恒等于360°,它与边数的多少无关.检测时间:120分钟 试题满分:100分 难度系数:0.55一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2024•邵阳模拟)如图,直线l1∥l2,分别与直线l交于点A,B,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=50°,则∠2的度数是( )A.130° B.100° C.90° D.70°解:如图,∵直线l1∥l2,∴∠1=∠3,∵∠1=50°,∴∠3=50°,由题意知∠4=30°,∴∠2=180°﹣∠3﹣∠4=180°﹣50°﹣30°=100°,故选:B.2.(2分)(2023秋•成华区期末)如图,直线AB∥CD,∠ABE=45°,∠E=20°,则∠D的度数为( )A.20° B.25° C.30° D.35°解:∵AB∥CD,∴∠ABE=∠BCD=45°,∴∠DCE=135°,由三角形的内角和可得∠D=180°﹣135°﹣20°=25°.故选:B.3.(2分)(2023秋•东城区期末)一个多边形的内角和等于外角和的两倍,那么这个多边形是( )A.三边形 B.四边形 C.五边形 D.六边形解:设这个多边形的边数为n,由题意得:(n﹣2)•180°=360°×2,n﹣2=4,n=6,故选:D.4.(2分)(2023秋•东莞市校级期末)为估计池塘两岸A、B间的距离,晓聪在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离可能是( )A.2m B.30m C.28m D.20m解:根据三角形的三边关系定理可得:16﹣12<AB<16+12,即4<AB<28,故选:D.5.(2分)(2023秋•桐乡市期末)如图,为了估计池塘两岸A,B间的距离,在池塘的一侧选取点P,测得PA=14 米,PB=9米,那么A,B间的距离不可能是( )A.6米 B.8.7米 C.27米 D.18米解:由三角形三边关系定理得:14﹣9<AB<14+9,5<AB<23,∴A,B间的距离不可能是27米.故选:C.6.(2分)(2023秋•射洪市期末)如图,下列条件中不能判定AB∥CD的是( )A.∠1=∠2 B.∠3=∠4 C.∠3+∠5=180° D.∠2=∠3解:A、∵∠1=∠2,∴∠3=∠5,因为”同旁内角互补,两直线平行“,所以本选项不能判断AB∥CD,符合题意;B、∵∠3=∠4,∴AB∥CD,故本选项能判定AB∥CD,不符合题意;C、∵∠3+∠5=180°,∴AB∥CD,故本选项能判定AB∥CD,不符合题意;D、∵∠1=∠5,∴AB∥CD,故本选项能判定AB∥CD,不符合题意.故选:A.7.(2分)(2023秋•太康县期末)如图,点E在CD延长线上,下列条件中不能判定AC∥BD的是( )A.∠1=∠2 B.∠3=∠4 C.∠5=∠C D.∠C+∠BDC=180°解:A.∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,所以A选项不符合题意.B.∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),不能判定BD∥AC,所以B选项符合题意.C.∵∠5=∠C,∴BD∥AC (同位角相等,两直线平行),所以C选项不合题意.D.∵∠C+∠BDC=180°,∴BD∥AC(同旁内角互补,两直线平行),所以D选项不合题意.故选:B.8.(2分)(2023秋•钟祥市校级期中)如图,∠AOB=70°,点M,N分别在OA,OB上运动(不与点O重合),ME平分∠AMN,ME的反向延长线与∠MNO的平分线交于点F,在M,N的运动过程中,∠F的度数( )A.变大 B.变小 C.等于55° D.等于35°解:∵ME平分∠AMN,NF平分∠MNO,∴∠EMN=∠AMN,∠MNF=∠MNO,根据外角的定义:∠AMN=∠AOB+∠MNO,∴∠EMN=∠AOB+∠MNO,∵∠AOB=70°,∴∠EMN=×70°+∠MNF=35°+∠MNF,根据外角的定义:∠EMN=∠F+∠MNF,∴∠F=35°,故选:D.9.(2分)(2023春•鼓楼区校级期末)如图,在△ABC,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC﹣∠C);④∠BGH=∠ABE+∠C,正确的是( )A.1 B.2 C.3 D.4解:设BD交FH于点J.①∵BD⊥FD,∴∠FJD+∠F=90°∵FH⊥BE,∴∠BJG+∠DBE=90°,∵∠FJD=∠BJG,∴∠DBE=∠F,①正确;②∵BE平分∠ABC,∴∠ABE=∠CBE,∠BEF=∠CBE+∠C,∴2∠BEF=∠ABC+2∠C,∠BAF=∠ABC+∠C,∴2∠BEF=∠BAF+∠C,②正确;③∠ABD=90°﹣∠BAC,∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,∵∠CBD=90°﹣∠C,∴∠DBE=∠BAC﹣∠C﹣∠DBE,由①得,∠DBE=∠F,∴∠F=∠BAC﹣∠C﹣∠DBE,∴∠F=(∠BAC﹣∠C);③正确;④∵∠AEB=∠EBC+∠C,∵∠ABE=∠CBE,∴∠AEB=∠ABE+∠C,∵BD⊥FC,FH⊥BE,∴∠FGD=∠FEB,∴∠BGH=∠ABE+∠C,④正确,故选:D.10.(2分)(2023秋•兰州期末)如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥EH于点G,且∠AFG=2∠D,则下列结论:①∠D=40°;②2∠D+∠EHC=90°;③FD平分∠HFB;④FH平分∠GFD.其中正确结论的个数是( )A.1个 B.2个 C.3个 D.4个解:延长FG,交CH于I.∵AB∥CD,∴∠BFD=∠D,∠AFI=∠FIH,∵FD∥EH,∴∠EHC=∠D,∵FE平分∠AFG,∴∠FIH=2∠AFE=2∠EHC,∴3∠EHC=90°,∴∠EHC=30°,∴∠D=30°,∴2∠D+∠EHC=2×30°+30°=90°,∴①∠D=40°错误;②2∠D+∠EHC=90°正确,∵FE平分∠AFG,∴∠AFI=30°×2=60°,∵∠BFD=30°,∴∠GFD=90°,∴∠GFH+∠HFD=90°,可见,∠HFD的值未必为30°,∠GFH未必为45°,只要和为90°即可,∴③FD平分∠HFB,④FH平分∠GFD不一定正确.故选:A.二.填空题(共10小题,满分20分,每小题2分)11.(2分)(2023秋•旌阳区期末)如图,在△ABC中,AD平分∠BAC交BC于点D,CE⊥AB于点E,若∠B=50°,∠ACE=20°,则∠ADC的度数是 85° .解:∵∠B=50°,CE⊥AB,∴∠BCE=90°﹣∠B=40°,∴∠ACB=∠BCE+∠ACE=40°+20°=60°,∴∠BAC=180°﹣∠B﹣∠ACB=70°.∵AD平分∠BAC,∴.∴∠ADC=180°﹣∠DAC﹣∠ACB=85°.故答案为:85°.12.(2分)(2023秋•鹰潭期末)如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.若∠A=30°,∠BDC=50°,则∠BDE的度数是 20° .解:∵∠A=30°,∠BDC=50°,∴∠ABD=∠BDC﹣∠A=20°.∵BD是△ABC的角平分线,∴∠DBC=∠ABD=20°,∵DE∥BC,∴∠BDE=∠DBC=20°.故答案为:20°.13.(2分)(2023秋•汉中期末)如图,BE,CF是△ABC的角平分线,∠ABC=60°,∠ACB=80°,BE,CF相交于点D,则∠CDE的度数是 70° .解:∵BE,CF是△ABC的角平分线,∠ABC=60°,∠ACB=80°,∴,,∴∠EDC=∠DBC+∠DCB=70°.故答案为:70°.14.(2分)(2023秋•石嘴山校级期中)如图,在五边形ABCDE中,∠A+∠B+∠E=310°,DP,CP分别平分∠EDC,∠BCD,则∠CPD的度数是 65° .解:∵五边形的内角和等于540°,∠A+∠B+∠E=310°,∴∠BCD+∠CDE=540°﹣310°=230°,∵∠BCD、∠CDE的平分线在五边形内相交于点P,∴∠PDC+∠PCD=(∠BCD+∠CDE)=115°,∴∠CPD=180°﹣115°=65°.故答案为:65°.15.(2分)(2023秋•钟祥市校级期中)一张△ABC纸片,点M、N分别是AB、AC上的点,若沿直线MN折叠后,点A落在AC边的下面A′的位置,如图所示,则∠1,∠2,∠A之间的数量关系式是 ∠1=2∠A+∠2 .解:如图,由折叠得:∠A=∠A′,∵∠1是△MDA的外角,∴∠1=∠A+∠MDA,同理:∠MDA=∠2+∠A′,∴∠1=∠A+∠2+∠A′,即:∠1=2∠A+∠2,故答案为:∠1=2∠A+∠2.16.(2分)(2023秋•湛江期末)如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是 80° .解:∵∠CAB的外角=∠B+∠C,且∠CAB的外角等于120°,∠B等于40°,∴∠C=80°,故答案为:80°.17.(2分)(2023秋•丹东期末)如图,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,∠D=15°,则∠A= 30° .解:∵∠ABC的平分线与∠ACE的平分线交于点D,∴∠ABD=∠CBD,∠ACD=∠ECD,∵∠ACE=∠A+∠ABC,即∠ACD+∠ECD=∠ABC+∠CBD+∠A,∴2∠ECD=2∠CBD+∠A,∴∠A=2(∠ECD﹣∠CBD)∵∠ECD=∠CBD+∠D,∠D=15°∴∠D=∠ECD﹣∠CBD=15°∴∠A=2×15°=30°.故答案为:30°.18.(2分)(2023秋•吉林期末)如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是 190° .解:如图,(9﹣2)×180°÷9×2=7×180°÷9×2=280°,∠3+∠4=180°﹣90°=90°,∠1+∠2=280°﹣90°=190°.故答案为:190°.19.(2分)(2022秋•济阳区期末)如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,以每秒2cm的速度沿A→C→E运动.若设点P运动的时间是t s,那么当t= 2或 s时,△APE的面积等于8.解:∵BC=8cm,点E是BC的中点,∴CE=BC=4cm,当点P在线段AC上,如图1所示,AP=2t,∵∠C=90°,∴S△APE=AP•CE=×2t×4=4t=8,解得:t=2;当点P在线段CE上,如图2所示,AC=6cm,PE=10﹣2t,∴S△APE=PE•AC=×(10﹣2t)×6=8,解得:t=.故答案为:2或.20.(2分)(2023春•慈溪市期中)如图,PQ∥MN,A,B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣4|+(b﹣1)2=0.若射线AM绕点A顺时针先转动18秒,射线BQ才开始绕点B逆时针旋转,在射线BQ到达BA之前,问射线AM再转动 或36 秒时,射线AM与射线BQ互相平行.解:∵|a−4|+(b−1)2=0,∴a=4,b=1,设射线AM再转动t秒时,射线AM、射线BQ互相平行.如图,射线AM绕点A顺时针先转动18秒后,AM转动至AM'的位置,∠MAM'=18×4=72°,分两种情况:①当M″到达MN前,∠QBQ'=t°,∠M'AM″=4t°,∵∠BAN=45°=∠ABQ,∴∠MAB=135°,∴∠M'AB=135°﹣72°=63°,∴∠ABQ'=45°﹣t°,∠BAM″=∠M'AM″﹣∠M'AB=4t°﹣63°,当∠ABQ'=∠BAM″时,BQ'∥AM″,此时,45°﹣t°=4t°﹣63°,解得t=;②当M″到达MN后,∠QBQ'=t°,∠NAM″=4t°﹣(180﹣72)°=4t°﹣108°,∠BAM″=45°﹣(4t°﹣108°)=153°﹣4t°,∵∠BAN=45°=∠ABQ,∴∠ABQ'=45°﹣t°,,当∠ABQ'=∠BAM″时,BQ'∥AM″,此时,45°﹣t°=153°﹣4t°,解得t=36;综上所述,射线AM再转动或36秒时,射线AM、射线BQ互相平行.故答案为:或36.三.解答题(共8小题,满分60分)21.(6分)(2023秋•德化县期末)如图,若∠DAE=∠E,∠B=∠D,那么AB∥DC吗?请在下面的解答过程中填空或在括号内填写理由.解:理由如下:∵∠DAE=∠E(已知),∴ AD ∥ BE ( 内错角相等,两直线平行 ),∴∠DCE= ∠D ( 两直线平行,内错角相等 ),又∵∠B=∠D(已知),∴∠DCE= ∠B ( 等量代换 ),∴AB∥DC( 同位角相等,两直线平行 ).解:∵∠DAE=∠E(已知),∴AD∥BE(内错角相等,两直线平行),∴∠DCE=∠D(两直线平行,内错角相等),又∵∠B=∠D(已知),∴∠DCE=∠B(等量代换),∴AB∥DC(同位角相等,两直线平行),故答案为:AD;BE;内错角相等,两直线平行;∠D;两直线平行,内错角相等;∠B;等量代换;同位角相等,两直线平行.22.(6分)(2023秋•商河县期末)如图,在△ABC中,∠AGF=∠ABC,∠1+∠2=180°.(1)求证:DE∥BF;(2)若DE⊥AC,∠2=140°,求∠AFG的度数.解:(1)BF∥DE,理由如下:∵∠AGF=∠ABC,∴GF∥BC,∴∠1=∠CBF,∵∠1+∠2=180°,∴∠CBF+∠2=180°,∴BF∥DE;(2)∵BF∥DE,DE⊥AC,∴BF⊥AC,∵∠1+∠2=180°,∠2=140°,∴∠1=40°,∴∠AFG=90°﹣40°=50°.23.(8分)(2023秋•凤翔区期末)如图,将一副三角板中的两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°.【观察猜想】(1)∠BCD与∠ACE的数量关系是 ∠BCD=∠ACE ;∠BCE与∠ACD的数量关系是 ∠BCE+∠ACD=180° ;【类比探究】(2)若保持三角板ABC不动,绕直角顶点C顺时针转动三角板DCE,试探究当∠ACD等于多少度时CE∥AB,画出图形并简要说明理由;【拓展应用】(3)若∠BCE=3∠ACD,求∠ACD的度数;并直接写出此时DE与AC的位置关系.解:(1)∵∠BCD+∠ACD=90°,∠ACE+∠ACD=90°,∴∠BCD=∠ACE;∵∠BCE=∠ACB+∠ACE=90°+∠ACE,∴∠BCE+∠ACD=90°+∠ACE+∠ACD=90°+90°=180°,∴∠BCE+∠ACD=180°.故答案为:∠BCD=∠ACE;∠BCE+∠ACD=180°;(2)分两种情况:①如图1所示,当CE∥AB时,∠ACE=∠A=30°,∴∠ACD=∠DCE﹣∠ACE=90°﹣30°=60°.②如图2所示,当CE∥AB时,∠BCE=∠B=60°,∴∠ACD=360°﹣∠ACB﹣∠BCE﹣∠DCE=360°﹣90°﹣60°﹣90°=120°.综上所述,当∠ACD等于60°或120°时,CE∥AB;(3)设∠ACD=α,则∠BCE=3α.由(1)可知,∠BCE+∠ACD=180°,∴3α+α=180°,∴α=45°,即∠ACD=45°,此时DE⊥AC或DE∥AC.24.(8分)(2023秋•鹰潭期末)生活现象如图1,杆秤是中国最古老也是现今人们仍然在使用的衡量工具,是利用杠杆原理来称质量的简易衡器,由木制的带有秤星的秤杆、金属秤砣、提绳等组成.数学模型如图2,是杆秤的示意图,AC∥BD,经测量发现∠A=104°,∠BOE=76°,请判断OE与BD的位置关系,并说明理由.解:OE∥BD,理由如下:∵AC∥BD,∴∠A+∠ABD=180°,∴∠ABD=180°﹣104°=76°,∴∠ABD=∠BOE,∴OE∥BD.25.(8分)(2023秋•城阳区期末)【发现问题】如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.【提出问题】小明提出:∠BPD,∠ABP和∠CDP三个角之间存在着怎样的数量关系?【分析问题】已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.【解决问题】探究一:请你帮小明解决这个问题,并说明理由.探究二:如图②,∠P,∠AMP,∠CNP的数量关系为 ∠BPD=∠ABP+∠CDP ;如图③,已知∠ABC=25°,∠C=60°,AE∥CD,则∠BAE= 145 °(不需要写解答过程)利用探究一得到的结论解决下列问题:如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P=2∠F,求∠FME的度数.解:探究一:∠BPD=∠ABP+∠CDP,理由如下:如图①,∵AB∥MN∥CD,∴∠BPN=∠ABP,∠DPN=∠CDP,∴∠BPN+∠DPN=∠ABP+∠CDP,∴∠BPD=∠ABP+∠CDP.探究二:如图②,∠AMP=∠P+∠CNP,理由如下:∵AB∥CD,∴∠MKP=∠CNP,∵∠AMP=∠P+∠MKP,∴∠AMP=∠P+∠CNP.如图③,延长EA交BC于L,∵AE∥CD,∴∠ALC=∠C=60°,∴∠ALB=180°﹣∠ALC=120°,∴∠BAE=∠B+∠ALB=25°+120°=145°.故答案为:∠AMP=∠P+∠CNP,145.∵射线ME,NF分别平分∠BMP和∠CNP,∴∠PME=∠PMB,∠CNF=∠PNF,如图④,由探究一的结论得:∠P=∠AMF+∠PMF+∠CNF+∠PNF,∠F=∠AMF+∠CNF,∵∠P=2∠F,∴∠AMF+∠PMF+∠CNF+∠PNF=2∠AMF+2∠CNF,∵∠CNF=∠PNF,∴∠AMF+∠PMF=2∠AMF,∴∠PMF=∠AMF=∠AMP,∴∠PMF+∠PME=(∠AMP+∠PMB),∴∠FME=∠AMB=×180°=90°.26.(8分)(2023秋•海口期末)将一副直角三角尺的直角顶点C按照如图方式叠放在一起(其中,∠A=60°,∠D=30°,∠E=∠B=45°),并能绕C点自由旋转.(1)写出∠ACB与∠DCE的数量关系,并说明理由;(2)当0°<∠ACE<180°且点E在直线AC的上方时,固定直角三角尺ACD,将直角三角尺ECB绕C点自由旋转.①当EB∥AC时,∠ACE= 45°或135° °;②要使CB∥AD,则∠ACE的度数为 30°或150° °,请说明理由;③直接写出分别使得CE∥AD,EB∥DC,EB∥AD的∠ACE的度数,在备用图中画出相应的草图,不必写出理由.解:(1)∠ACB与∠DCE的数量关系是:∠ACB+∠DCE=180°,理由如下:∵∠A=60°,∠D=30°,∠E=∠B=45°,∴∠ACD=90°,∠BCE=90°,∴∠ACB=∠ACD+∠DCB=90°+∠DCB,∠DCE=∠BCE﹣∠DCB=90°﹣∠DCB,∴∠ACB+∠DCE=90°+∠DCB+90°﹣∠DCB=180°;(2)①当EB∥AC时,有以下两种情况:(ⅰ)当BE在AC的上方时,如图1所示:∵EB∥AC,∠E=45°,∴∠ACE=∠E=45°,(ⅱ)当BE在AC下方时,如图2所示:∵EB∥AC,∠B=45°,∴∠ACB=∠B=45°,∴∠ACE=∠ACB+∠BCE=45°+90°=135°,综上所述:∠ACE=45°或135°,故答案为:45°或135°.②要使CB∥AD,则∠ACE的度数为60°或150°,理由如下:有以下两种情况:(ⅰ)当CB在AC的上方时,如图3所示:∵CB∥AD,∠D=30°,∴∠DCB=∠D=30°,∴∠DCE=∠BCE﹣∠DCB=90°﹣30°=60°,∴∠ACE=∠ACD﹣∠DCE=90°﹣60°=30°;(ⅱ)当CB在AC的下方时,如图4所示:∵CB∥AD,∠A=60°,∴∠ACB=∠A=60°,∴∠ACE=∠ACB+∠BCE=60°+90°=150°,综上所述:∠ACE的度数为30°或150°;故答案为:60°或150°.③当CE∥AD时,有以下两种情况:(ⅰ)当CE在AC上方时,如图5所示:∵CE∥AD,∠D=30°,∴∠DCE=∠D=30°,∴∠ACE=∠ACD+∠DCE=90°+30°=120°;(ⅱ)当CE在AC下方时,如图6所示:∵CE∥AD,∠A=60°,∴∠ACE=∠A=60°,综上所述:当CE∥AD时,∠ACE的度数为120°或60°;当EB∥DC时,有以下两种情况:(ⅰ)当BE在CD的左侧时,如图7所示:∵EB∥DC,∠B=45°,∴∠BCD=∠B=45°,∴∠ACB=∠ACD﹣∠BCD=90°﹣45°=45°,∴∠ACE=∠BCE﹣∠ACB=90°﹣45°=45°,(ⅱ)当BE在CD的右侧时,如图8所示:∵EB∥DC,∠E=45°,∴∠DCE=∠E=45°,∴∠ACE=∠ACD+∠DCE=90°+45°=135°,综上所述:当EB∥DC时,∠ACE的度数为45°或135°;当EB∥AD时,有以下两种情况:(ⅰ)当EB在AD的左侧时,如图9所示:设BC与AD交于点T,∵EB∥AD,∠B=45°,∴∠ATC=∠B=45°,∴∠ACT=180°﹣(∠ATC+∠A)=180°﹣(45°+60°)=75°,∴∠ACE=∠BCE﹣∠ACT=90°﹣75°=15°,(ⅱ)当EB在AD的右侧时,如图10所示:延长AC交EB于点H,∵EB∥AD,∠A=60°,∴∠CHE=180°﹣∠A=180°﹣60°=120°,∴∠ECH=180°﹣(CHE+∠E)=180°﹣(120°+45°)=15°,∵∠ACD=90°,∴∠DCH=90°,∴∠DCE=∠DCH﹣∠ECH=90°﹣15°=75°,∴∠ACE=∠ACD+∠DCE=90°+75°=165°,综上所述:当EB∥AD时,∠ACE的度数为15°或165°.∴当CE∥AD时,∠ACE的度数为120°或60°;当EB∥DC时,∠ACE的度数为45°或135°;当EB∥AD时,∠ACE的度数为15°或165°.27.(8分)(2023秋•大东区期末)如图,四边形BCED中,点A在CB的延长线上,点F在DE的延长线上,连接AF交BD于G,交CE于H,且∠1=45°,∠2=135°.(1)求证:BD∥CE;(2)若∠C=∠D,求证:∠A=∠F.证明:(1)∵∠CHG+∠2=180°,∠2=135°,∴∠CHG=45°,∵∠1=45°,∴∠CHG=∠1,∴BD∥CE.(2)∵BD∥CE,∴∠C=∠ABD,∵∠C=∠D,∴∠ABD=∠D.∴AC∥DF,∴∠A=∠F.28.(8分)(2023秋•潍城区期末)已知ABCD为四边形,点E为边AB延长线上一点.【探究】:(1)如图1,∠ADC=110°,∠BCD=120°,∠DAB和∠CBE的平分线交于点F,则∠AFB= 35 °;(2)如图2,∠ADC=α,∠BCD=β,且α+β>180°,∠DAB和∠CBE的平分线交于点F,则∠AFB= ;(用α,β表示)(3)如图3,∠ADC=α,∠BCD=β,当∠DAB和∠CBE的平分线AG,BH平行时,α,β应该满足怎样的数量关系?请证明你的结论;【挑战】:如果将(2)中的条件α+β>180°改为α+β<180°,再分别作∠DAB和∠CBE的平分线,若两平分线所在的直线交于点F,则∠AFB与α,β有怎样的数量关系?请画出图形并直接写出结论.解:(1)如图1.∵BF平分∠CBE,AF平分∠DAB,∴∠FBE=∠CBE,∠FAB=∠DAB.∵∠D+∠DCB+∠DAB+∠ABC=360°,∴∠DAB+∠ABC=360°﹣∠D﹣∠DCB=360°﹣120°﹣110°=130°.又∵∠F+∠FAB=∠FBE,∴∠F=∠FBE﹣∠FAB===(180°﹣130°)=25°;(2)如图2.由(1)得:∠AFB=,∠DAB+∠ABC=360°﹣∠D﹣∠DCB.∴∠AFB==.(3)若AG∥BH,则α+β=180°.证明:如图3.若AG∥BH,则∠GAB=∠HBE.∵AG平分∠DAB,BH平分∠CBE,∴∠DAB=2∠GAB,∠CBE=2∠HBE.∴∠DAB=∠CBE.∴AD∥BC.∴∠DAB+∠DCB=α+β=180°.挑战:如图4.∵AM平分∠DAB,BN平分∠CBE,∴∠BAM=,.∵∠D+∠DAB+∠ABC+∠BCD=360°,∴∠DAB+∠ABC=360°﹣∠D﹣BCD=360°﹣α﹣β.∴∠DAB+180°﹣∠CBE=360°﹣α﹣β.∴∠DAB﹣∠CBE=180°﹣α﹣β.∵∠ABF与∠NBE是对顶角,∴∠ABF=∠NBE.又∵∠F+∠ABF=∠MAB,∴∠F=∠MAB﹣∠ABF.∴∠F===90°﹣
相关资料
更多









