资料中包含下列文件,点击文件名可预览资料内容




还剩13页未读,
继续阅读
成套系列资料,整套一键下载
第11章《一元一次不等式》-2023-2024学年数学七年级下册章节复习讲讲义(苏科版)
展开
这是一份第11章《一元一次不等式》-2023-2024学年数学七年级下册章节复习讲讲义(苏科版),文件包含第11章一元一次不等式教师版docx、第11章一元一次不等式学生版docx等2份学案配套教学资源,其中学案共24页, 欢迎下载使用。
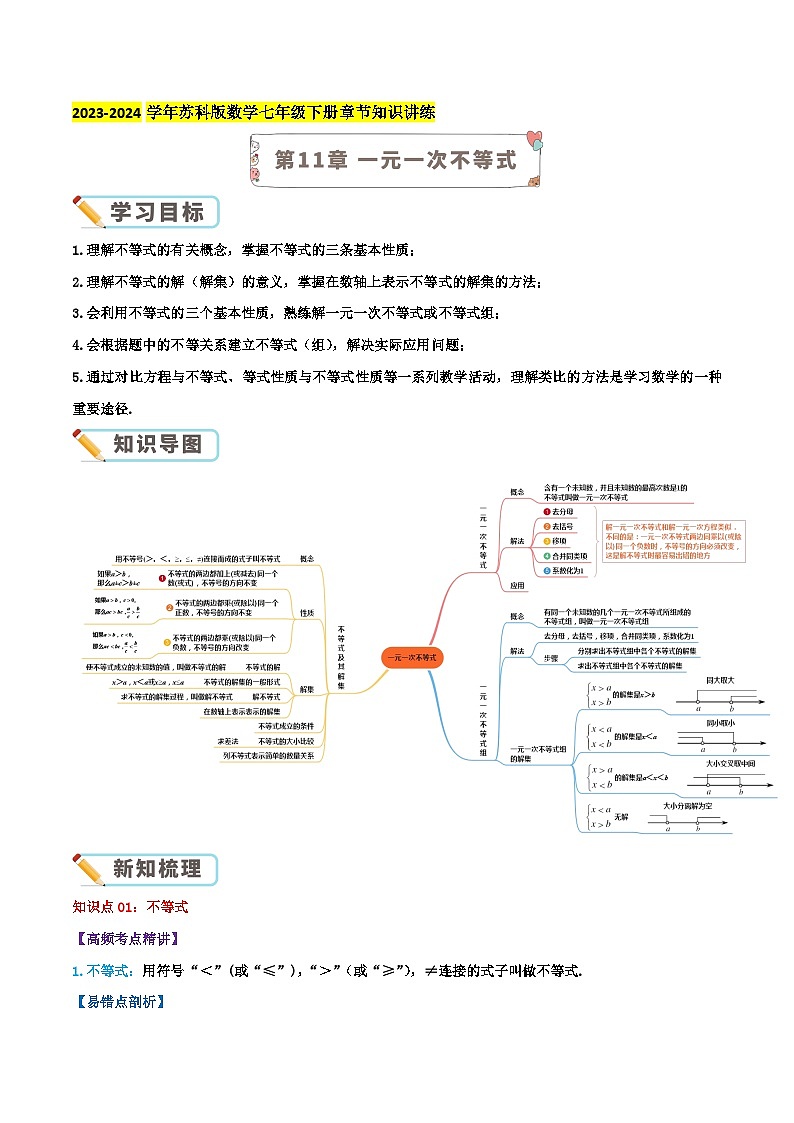
2023-2024学年苏科版数学七年级下册章节知识讲练1.理解不等式的有关概念,掌握不等式的三条基本性质;2.理解不等式的解(解集)的意义,掌握在数轴上表示不等式的解集的方法;3.会利用不等式的三个基本性质,熟练解一元一次不等式或不等式组; 4.会根据题中的不等关系建立不等式(组),解决实际应用问题;5.通过对比方程与不等式、等式性质与不等式性质等一系列教学活动,理解类比的方法是学习数学的一种重要途径.知识点01:不等式【高频考点精讲】1.不等式:用符号“<”(或“≤”),“>”(或“≥”),≠连接的式子叫做不等式.【易错点剖析】(1)不等式的解:能使不等式成立的未知数的值叫做不等式的解.(2)不等式的解集:对于一个含有未知数的不等式,它的所有解组成这个不等式的解集.解集的表示方法一般有两种:一种是用最简的不等式表示,例如,等;另一种是用数轴表示,如下图所示:(3)解不等式:求不等式的解集的过程叫做解不等式.2. 不等式的性质:不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.用式子表示:如果a>b,那么a±c>b±c不等式的基本性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.用式子表示:如果a>b,c>0,那么ac>bc(或).不等式的基本性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.用式子表示:如果a>b,c<0,那么ac<bc(或).知识点02:一元一次不等式【高频考点精讲】1. 定义:不等式的左右两边都是整式,经过化简后只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式,【易错点剖析】ax+b>0或ax+b<0(a≠0)叫做一元一次不等式的标准形式.2.解法:解一元一次不等式步骤:去分母、去括号、移项、合并同类项、系数化为1. 【易错点剖析】不等式解集的表示:在数轴上表示不等式的解集,要注意的是“三定”:一是定边界点,二是定方向,三是定空实.3.应用:列不等式解应用题的基本步骤与列方程解应用题的步骤相类似,即:(1)审:认真审题,分清已知量、未知量;(2)设:设出适当的未知数;(3)找:找出题中的不等关系,要抓住题中的关键字,如“大于”“小于”“不大于”“至少”“不超过”“超过”等关键词的含义;(4)列:根据题中的不等关系,列出不等式;(5)解:解出所列的不等式的解集;(6)答:检验是否符合题意,写出答案.【易错点剖析】列一元一次不等式解应用题时,经常用到“合算”、“至少”、“不足”、“不超过”、“不大于”、“不小于”等表示不等关系的关键词语,弄清它们的含义是列不等式解决问题的关键.知识点03:一元一次不等式组 【高频考点精讲】 关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组. 【易错点剖析】(1)不等式组的解集:不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集.(2)解不等式组:求不等式组解集的过程,叫做解不等式组. (3)一元一次不等式组的解法:分别解出各不等式,把解集表示在数轴上,取所有解集的公共部分,利用数轴可以直观地表示不等式组的解集. (4)一元一次不等式组的应用: ①根据题意构建不等式组,解这个不等式组;②由不等式组的解集及实际意义确定问题的答案.检测时间:120分钟 试题满分:100分 难度系数:0.55一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2023秋•姑苏区期末)若a>b,则下列不等式变形错误的是( )A.a﹣1>b﹣1 B. C.3a>3b D.1﹣a>1﹣b解:A、∵a>b,∴a﹣1>b﹣1,故正确,不合题意;B、∵a>b,∴,故正确,不合题意;C、∵a>b,∴3a>3b,故正确,不合题意;D、∵a>b,∴﹣a<﹣b,∴1﹣a<1﹣b,故错误,符合题意;故选:D.2.(2分)(2023秋•奉化区校级期中)若关于x的不等式组的整数解共有4个,则m的取值范围是( )A.6<m<7 B.6≤m<7 C.6≤m≤7 D.6<m≤7解:由7﹣2x≤1得,x≥3,∵x<m,故原不等式组的解集为:3≤x<m,∵不等式组的正整数解有4个,∴其整数解应为:3、4、5、6,∴m的取值范围是6<m≤7.故选:D.3.(2分)(2023秋•永州期末)已知关于x的不等式整数解共有2个,若m为整数,则m=( )A.2 B.3 C.4 D.5解:由x﹣m<0,得:x<m,由5﹣2x≤1,得:x≥2,∵不等式组有2个整数解,∴不等式组的整数解为2、3,∴3<m≤4,又∵m为整数,∴m=4,故选:C.4.(2分)(2022秋•新化县期末)方程组的解满足不等式x﹣y<5,则a的范围是( )A.a<1 B.a>1 C.a<2 D.a>2解:,①+②,得3x﹣3y=3+6a,化简,得x﹣y=1+2a,∵x﹣y<5,∴1+2a<5,解得,a<2,故选:C.5.(2分)(2022秋•新田县期末)若关于x的不等式组恰有3个整数解,则实数a的取值范围是( )A.7<a<8 B.7≤a<8 C.7<a≤8 D.7≤a≤8解:,解不等式①,得:x>4.5,解不等式②,得:x<a,由题意可知,不等式组有解集,∴该不等式组的解集是4.5<x<a,∵不等式组恰有3个整数解,∴这三个整数解是5,6,7,∴7<a≤8,故选:C.6.(2分)(2023秋•沙坪坝区校级期末)如果不等式(a﹣5)x<a﹣5的解集为x>1,则a必须满足的条件是( )A.a>0 B.a>5 C.a≠5 D.a<5解:∵不等式(a﹣5)x<a﹣5的解集为x>1,∴a﹣5<0,∴a<5,故选:D.7.(2分)(2023春•自贡期末)若关于x的不等式组有100个整数解,则a的取值范围是( )A.﹣1449<a≤﹣1448 B.﹣1449≤a<﹣1448 C.﹣1450≤a<﹣1449 D.﹣1450<a≤﹣1449解:解不等式x﹣a≥2023,得:x≥2023+a,解不等式2024﹣x>2x﹣1,得:x<675,∵不等式组100个整数解,∴574<2023+a≤575,∴﹣1449<a≤﹣1448,故选:A.8.(2分)(2023春•那曲市期末)若关于x的一元一次不等式组有解,则k的取值范围是( )A.k≤3 B.k<3 C.k<2 D.k≤2解:,解①得x<2,解②得x>k﹣1,因为关于x的一元一次不等式组有解,所以k﹣1<2,解得k<3.故选:B.9.(2分)(2023春•吕梁期末)若关于x的方程的解为正数,且a使得关于y的不等式组恰有两个整数解,则所有满足条件的整数a的值的和是( )A.0 B.1 C.2 D.3解:由方程可得,x=,∵方程的解为正数,∴>0,∴a<,由y+3>1得y>﹣2,由3y﹣a<1得y<,∵a使得关于y的不等式组恰有两个整数解,∴这两个整数解为﹣1,0,∴0<≤1,解得﹣1<a≤2,由上可得﹣1<a<,∴所有满足条件的整数a的值为0,1,∵0+1=1,∴所有满足条件的整数a的值和为1,故选:B.10.(2分)(2023秋•姑苏区校级期末)如果关于y的方程有非负整数解,且关于x的不等式组的解集为x≥1,则所有符合条件的整数a的和为( )A.﹣5 B.﹣8 C.﹣9 D.﹣12解:,解得:,∵关于y的方程有非负整数解,∴,解得:a≥﹣5,且为整数,关于x的不等式组整理得:,∵不等式组的解集为x≥1,∴a+4≤1,解得:a≤﹣3,∴﹣5≤a≤﹣3且为整数,∴a=﹣5,﹣3,于是符合条件的所有整数a的值之和为:﹣5﹣3=﹣8.故选:B.二.填空题(共10小题,满分20分,每小题2分)11.(2分)(2023秋•惠州期末)不等式组:的解集是 .解:,解不等式①,得x,解不等式②,得x<2,故不等式组的解集为.故答案为:.12.(2分)(2023春•集美区校级期中)若不等式(a﹣1)x>1﹣a的解集是x<﹣1,则a的取值范围是 a<1 .解:两边同时除以(a﹣1)得,x<﹣1,可见,a﹣1<0,解得a<1.故答案为a<1.13.(2分)(2023秋•海曙区期中)不等式组的解集为x>3,则k的取值范围为 k≤2 .解:由3x﹣9>0得:x>3,由x>k+1且不等式组的解集为x>3,知k+1≤3,解得k≤2,故答案为:k≤2.14.(2分)(2023春•富锦市校级期末)已知关于x的不等式组的所有整数解的和为﹣9,m的取值范围是 3≤m<6或﹣6≤m<﹣3 .解:解不等式3x+m<0,得:x<﹣,∵x>﹣5,∴不等式组的解集为﹣5<x<﹣,∵不等式的所有整数解的和为﹣9,∴不等式组的整数解为﹣4、﹣3、﹣2或﹣4、﹣3、﹣2,﹣1,0,1,则﹣2<﹣≤﹣1或1<﹣≤2,解得3≤m<6或﹣6≤m<﹣3,故答案为:3≤m<6或﹣6≤m<﹣3.15.(2分)(2023秋•新田县期末)关于x的不等式组恰有3个整数解,则a的取值范围是 2≤a<3 .解:,解①得:x>a﹣2,解②得:x≤3.∵不等式组恰有3个整数解,∴不等式组的整数解是:1,2,3.∴0≤a﹣2<1,∴2≤a<3.故答案为:2≤a<3.16.(2分)(2023秋•鄞州区期中)若不等式(a﹣1)x<a﹣1的解集是x>1,则a的取值范围是 a<1 .解:∵不等式(a﹣1)x<a﹣1的解集是x>1,∴a﹣1<0,解得a<1.故答案为:a<1.17.(2分)(2023春•渝中区校级期末)关于x的不等式组的解集为x≥3,且关于x的一次方程5x﹣a=x+3有非负整数解,则所有满足条件的整数a的和为 ﹣2 .解:将一元一次不等式组整理得到:,∵不等式组的解集为x≥3,∴a﹣2<3,∴a<5;解关于x的一次方程5x﹣a=x+3得x=.∵x有非负整数解,∴≥0,解得:a≥﹣3,∴﹣3≤a<5,∴满足条件的整数a为:﹣3,1,∴所有满足条件的整数a的和为:﹣3+1=﹣2.故答案为:﹣2.18.(2分)(2023春•重庆期中)若关于x的一元一次方程有正整数解,且使关于x的不等式组至少有4个整数解,求出满足条件的整数a的所有值的积为 15 .解:解不等式2x﹣a≥0,得x≥,解不等式,得x<8,∵不等式组至少有4个整数解,∴≤4,解得a≤8,解关于x的一元一次方程,得x=,∵方程有正整数解,∴>0,则a>0,∴0<a≤8,其中能使为正整数的a值有1,3,5,其积为1×3×5=15.故答案为:15.19.(2分)(2022春•渝中区校级月考)清明将至,前去扫墓的人逐渐增多.某花店购进白菊,白百合,马蹄莲共计m捆.白菊每捆20支,白百合每捆12支,马蹄莲每捆10支.现取出白菊的,白百合的,马蹄莲的,全部用于扎成A、B两款花束销售.其中A款花束白菊2支,白百合3支,马蹄莲1支,B款花束白菊5支,马蹄莲2支.如此取出后剩下的白百合支数不多于马蹄莲支数,则购进的白菊捆数与白百合捆数之比至少为 3:5 .解:设购进白菊有x捆,白百何有y捆,则马蹄莲有(m﹣x﹣y)捆,∵白菊每捆20支,白百合每捆12支,马蹄莲每捆10支,∴白菊有20x支,白百合有12y支,马蹄莲有10(m﹣x﹣y)支,∵现取出白菊的,白百合的,马蹄莲的,全部用于扎成A、B两款花束销售,∴取出的白菊有10x支,白百合有4y支,马蹄莲有(m﹣x﹣y)支,设A款花束有a束,B款花束有b束,根据A款花束白菊2支,白百合3支,马蹄莲1支,B款花束白菊5支,马蹄莲2支可列方程组得:,由②得:a= ④,把④代入①得:b=2x﹣y ⑤,把④和⑤代入③得:m=,∵取出后剩下的白百合支数不多于马蹄莲支数,∴12y﹣4y≤10(m﹣x﹣y)﹣(m﹣x﹣y),即8y≤(﹣x﹣y),整理得:5x≥3y,∴,故答案为:3:5.20.(2分)(2022春•梁园区期末)对于x,符号[x]表示不大于x的最大整数.如:[3.14]=3,[﹣7.59]=﹣8,则满足关系式的x的整数值有 3 个.解:由题意得4≤<5,解得:7≤x<,其整数解为7、8、9共3个.故答案为:3.三.解答题(共8小题,满分60分)21.(6分)(2023秋•桐乡市期末)解不等式,并把解在数轴上表示出来.解:,3(﹣3+x)≤2(2x﹣4),﹣9+3x≤4x﹣8,3x﹣4x≤9﹣8,﹣x≤1,x≥﹣1.将不等式的解集表示在数轴上如下:22.(6分)(2023秋•钢城区期末)解不等式组:,并求出它的非负整数解.解:由①得:x<2,由②得:x≥﹣1,∴不等式组的解集为﹣1≤x<2,则不等式组的非负整数解为0,1.23.(8分)(2023秋•邵阳期末)已知关于x的不等式组;(1)若该不等式组有且只有三个整数解,求a的取值范围;(2)若该不等式组有解,且它的解集中的任何一个值均不在x≥5的范围内,求a的取值范围.解:(1),解不等式①,得:x>2,解不等式②,得:x<7﹣a,∴不等式组的解集为2<x<7﹣a,又∵不等式组有且只有三个整数解,∴5<7﹣a≤6,解得:1≤a<2;(2)由(1)可得,不等式组的解集为2<x<7﹣a,∵不等式组有解,∴7﹣a>2,解得:a<5,又∵它的解集中的任何一个值均不在x≥5的范围内,∴7﹣a≤5,解得:a≥2,∴a的取值范围2≤a<5.24.(8分)(2023春•大竹县校级期末)我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<﹣2.5>=﹣2.根据上述规定,解决下列问题:(1)[﹣4.5]= ﹣5 ,<3.01>= 4 ;(2)若x为整数,且[x]+<x>=2017,求x的值;(3)若x、y满足方程组,求x、y的取值范围.解:(1)由题可得[﹣4.5]=﹣5,<3.01>=4,故答案为:﹣5,4;(2)∵[x]≤x,且x为整数,∴[x]=x,∵<x>>x,且x为整数,∴<x>=x+1,∵[x]+<x>=2017,∴x+(x+1)=2017,解得x=1008;(3)解原方程组,得,又∵[x]表示不大于x的最大整数,<x>表示大于x的最小整数,∴﹣1≤x<0,2≤y<3.25.(8分)(2024•邵阳模拟)某商场同时采购了A,B两种品牌的运动装,第一次采购A品牌运动装10件,B品牌运动装30件,采购费用为8600元;第二次只采购了B品牌运动装50件,采购费用为11000元.(1)求A,B两种品牌运动装的采购单价分别为多少元每件?(2)商家通过一段时间的营销后发现,B品牌运动装的销售明显比A品牌好,商家决定采购一批运动装,要求:①采购B品牌运动装的数量是A品牌运动装的2倍多10件,且A品牌的采购数量不低于18件;②采购两种品牌运动装的总费用不超过15000元,请问该商家有哪几种采购方案?解:(1)设A品牌运动装的采购单价是x元/件,B品牌运动装的采购单价是y元/件,根据题意得:,解得:.答:A品牌运动装的采购单价是200元/件,B品牌运动装的采购单价是220元/件;(2)设该商家采购A品牌运动装m件,则采购B品牌运动装(2m+10)件,根据题意得:,解得:18≤m≤20,又∵m为正整数,∴m可以为18,19,20,∴该商家共有3种采购方案,方案1:采购A品牌运动装18件,B品牌运动装46件;方案2:采购A品牌运动装19件,B品牌运动装48件;方案3:采购A品牌运动装20件,B品牌运动装50件.26.(8分)(2023•曲靖一模)2022年1月7日,《云南省全民健身实施计划(2021﹣2025年)》新闻发布会顺利举行.会议上就“十四五”时期深化体育改革,推进新时代全民健身高质量发展作了全面部署和安排.其中,“强化供给,补齐全民健身设施建设短板”是《云南省全民健身实施计划(2021﹣2025年)》的主要任务之一.春城小区计划购买10台健身器材供小区居民锻炼使用,了解到购买1台B型健身器材比1台A型健身器材贵200元,购买2台A型健身器材和5台B型健身器材共花8000元.(1)A型健身器材和B型健身器材的单价是多少钱?(2)春城小区计划购买B型健身器材的数量不超过A型健身器材的数量的2倍,购买资金不低于10800元,请问共有哪几种购买方案,哪一种方案最省钱.解:(1)设A型健身器材的单价是x元,B型健身器材的单价是y元,依题意得:,解得:.答:A型健身器材的单价是1000元,B型健身器材的单价是1200元.(2)设购买m台A型健身器材,则购买(10﹣m)台B型健身器材,依题意得:,解得:≤m≤6.又∵m为整数,∴m可以为4,5,6,∴共有3种购买方案,方案1:购买4台A型健身器材,6台B型健身器材,所需购买资金为1000×4+1200×6=11200(元);方案2:购买5台A型健身器材,5台B型健身器材,所需购买资金为1000×5+1200×5=11000(元);方案3:购买6台A型健身器材,4台B型健身器材,所需购买资金为1000×6+1200×4=10800(元).∵11200>11000>10800,∴最省钱的购物方案为:购买6台A型健身器材,4台B型健身器材.27.(8分)(2023•金凤区校级二模)围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有4000多年的历史,中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为活跃学生课余生活,欲购买一批象棋和围棋,已知购买3副象棋和1副围棋共需125元,购买2副象棋和3副围棋共需165元.(1)求每副象棋和围棋的价格;(2)若学校准备购买象棋和围棋总共100副,且总费用不超过3200元,则最多能购买多少副围棋?解:(1)设每副象棋的价格为x元,每副围棋的价格为y元.依题意得,解得.答:每副象棋的价格为30元,每副围棋的价格为35元.(2)设购买m副围棋,则购买(100﹣m)副象棋.依题意得:30(100﹣m)+35m≤3200,解得m≤40.答:最多能购买40副围棋.28.(8分)(2022秋•婺城区期末)为更好地推进生活垃圾分类工作,改善城市生态环境,某小区准备购买A、B两种型号的垃圾箱,通过对市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需390元,购买2个A型垃圾箱比购买1个B型垃圾箱少用20元.(1)求每个A型垃圾箱和每个B型垃圾箱分别多少元?(2)该小区计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个,且A型号垃圾箱个数不多于B型垃圾箱个数的3倍,则该小区购买A、B两种型号垃圾箱的方案有哪些?解:(1)设每个A型垃圾箱x元,每个B型垃圾箱y元.依题意,得:,解得:.答:每个A型垃圾箱50元,每个B型垃圾箱120元;(2)设购买m个B型垃圾箱,则购买(20﹣m)个A型垃圾箱.依题意,得:,解得:5≤m≤.又m为整数,m可以为5,6,7,∴有3种购买方案:方案1:购买15个A型垃圾箱,购买5个B型垃圾箱;方案2:购买14个A型垃圾箱,购买6个B型垃圾箱;方案3:购买13个A型垃圾箱,购买7个B型垃圾箱
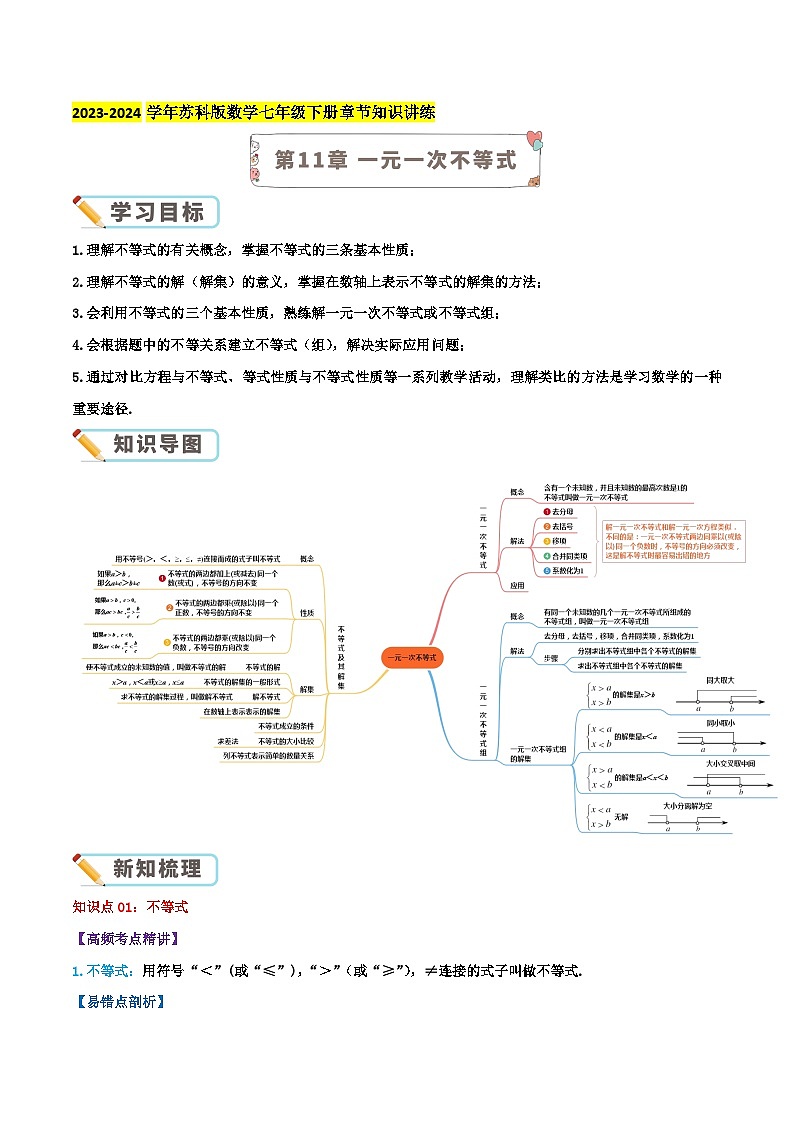
2023-2024学年苏科版数学七年级下册章节知识讲练1.理解不等式的有关概念,掌握不等式的三条基本性质;2.理解不等式的解(解集)的意义,掌握在数轴上表示不等式的解集的方法;3.会利用不等式的三个基本性质,熟练解一元一次不等式或不等式组; 4.会根据题中的不等关系建立不等式(组),解决实际应用问题;5.通过对比方程与不等式、等式性质与不等式性质等一系列教学活动,理解类比的方法是学习数学的一种重要途径.知识点01:不等式【高频考点精讲】1.不等式:用符号“<”(或“≤”),“>”(或“≥”),≠连接的式子叫做不等式.【易错点剖析】(1)不等式的解:能使不等式成立的未知数的值叫做不等式的解.(2)不等式的解集:对于一个含有未知数的不等式,它的所有解组成这个不等式的解集.解集的表示方法一般有两种:一种是用最简的不等式表示,例如,等;另一种是用数轴表示,如下图所示:(3)解不等式:求不等式的解集的过程叫做解不等式.2. 不等式的性质:不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.用式子表示:如果a>b,那么a±c>b±c不等式的基本性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.用式子表示:如果a>b,c>0,那么ac>bc(或).不等式的基本性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.用式子表示:如果a>b,c<0,那么ac<bc(或).知识点02:一元一次不等式【高频考点精讲】1. 定义:不等式的左右两边都是整式,经过化简后只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式,【易错点剖析】ax+b>0或ax+b<0(a≠0)叫做一元一次不等式的标准形式.2.解法:解一元一次不等式步骤:去分母、去括号、移项、合并同类项、系数化为1. 【易错点剖析】不等式解集的表示:在数轴上表示不等式的解集,要注意的是“三定”:一是定边界点,二是定方向,三是定空实.3.应用:列不等式解应用题的基本步骤与列方程解应用题的步骤相类似,即:(1)审:认真审题,分清已知量、未知量;(2)设:设出适当的未知数;(3)找:找出题中的不等关系,要抓住题中的关键字,如“大于”“小于”“不大于”“至少”“不超过”“超过”等关键词的含义;(4)列:根据题中的不等关系,列出不等式;(5)解:解出所列的不等式的解集;(6)答:检验是否符合题意,写出答案.【易错点剖析】列一元一次不等式解应用题时,经常用到“合算”、“至少”、“不足”、“不超过”、“不大于”、“不小于”等表示不等关系的关键词语,弄清它们的含义是列不等式解决问题的关键.知识点03:一元一次不等式组 【高频考点精讲】 关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组. 【易错点剖析】(1)不等式组的解集:不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集.(2)解不等式组:求不等式组解集的过程,叫做解不等式组. (3)一元一次不等式组的解法:分别解出各不等式,把解集表示在数轴上,取所有解集的公共部分,利用数轴可以直观地表示不等式组的解集. (4)一元一次不等式组的应用: ①根据题意构建不等式组,解这个不等式组;②由不等式组的解集及实际意义确定问题的答案.检测时间:120分钟 试题满分:100分 难度系数:0.55一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2023秋•姑苏区期末)若a>b,则下列不等式变形错误的是( )A.a﹣1>b﹣1 B. C.3a>3b D.1﹣a>1﹣b解:A、∵a>b,∴a﹣1>b﹣1,故正确,不合题意;B、∵a>b,∴,故正确,不合题意;C、∵a>b,∴3a>3b,故正确,不合题意;D、∵a>b,∴﹣a<﹣b,∴1﹣a<1﹣b,故错误,符合题意;故选:D.2.(2分)(2023秋•奉化区校级期中)若关于x的不等式组的整数解共有4个,则m的取值范围是( )A.6<m<7 B.6≤m<7 C.6≤m≤7 D.6<m≤7解:由7﹣2x≤1得,x≥3,∵x<m,故原不等式组的解集为:3≤x<m,∵不等式组的正整数解有4个,∴其整数解应为:3、4、5、6,∴m的取值范围是6<m≤7.故选:D.3.(2分)(2023秋•永州期末)已知关于x的不等式整数解共有2个,若m为整数,则m=( )A.2 B.3 C.4 D.5解:由x﹣m<0,得:x<m,由5﹣2x≤1,得:x≥2,∵不等式组有2个整数解,∴不等式组的整数解为2、3,∴3<m≤4,又∵m为整数,∴m=4,故选:C.4.(2分)(2022秋•新化县期末)方程组的解满足不等式x﹣y<5,则a的范围是( )A.a<1 B.a>1 C.a<2 D.a>2解:,①+②,得3x﹣3y=3+6a,化简,得x﹣y=1+2a,∵x﹣y<5,∴1+2a<5,解得,a<2,故选:C.5.(2分)(2022秋•新田县期末)若关于x的不等式组恰有3个整数解,则实数a的取值范围是( )A.7<a<8 B.7≤a<8 C.7<a≤8 D.7≤a≤8解:,解不等式①,得:x>4.5,解不等式②,得:x<a,由题意可知,不等式组有解集,∴该不等式组的解集是4.5<x<a,∵不等式组恰有3个整数解,∴这三个整数解是5,6,7,∴7<a≤8,故选:C.6.(2分)(2023秋•沙坪坝区校级期末)如果不等式(a﹣5)x<a﹣5的解集为x>1,则a必须满足的条件是( )A.a>0 B.a>5 C.a≠5 D.a<5解:∵不等式(a﹣5)x<a﹣5的解集为x>1,∴a﹣5<0,∴a<5,故选:D.7.(2分)(2023春•自贡期末)若关于x的不等式组有100个整数解,则a的取值范围是( )A.﹣1449<a≤﹣1448 B.﹣1449≤a<﹣1448 C.﹣1450≤a<﹣1449 D.﹣1450<a≤﹣1449解:解不等式x﹣a≥2023,得:x≥2023+a,解不等式2024﹣x>2x﹣1,得:x<675,∵不等式组100个整数解,∴574<2023+a≤575,∴﹣1449<a≤﹣1448,故选:A.8.(2分)(2023春•那曲市期末)若关于x的一元一次不等式组有解,则k的取值范围是( )A.k≤3 B.k<3 C.k<2 D.k≤2解:,解①得x<2,解②得x>k﹣1,因为关于x的一元一次不等式组有解,所以k﹣1<2,解得k<3.故选:B.9.(2分)(2023春•吕梁期末)若关于x的方程的解为正数,且a使得关于y的不等式组恰有两个整数解,则所有满足条件的整数a的值的和是( )A.0 B.1 C.2 D.3解:由方程可得,x=,∵方程的解为正数,∴>0,∴a<,由y+3>1得y>﹣2,由3y﹣a<1得y<,∵a使得关于y的不等式组恰有两个整数解,∴这两个整数解为﹣1,0,∴0<≤1,解得﹣1<a≤2,由上可得﹣1<a<,∴所有满足条件的整数a的值为0,1,∵0+1=1,∴所有满足条件的整数a的值和为1,故选:B.10.(2分)(2023秋•姑苏区校级期末)如果关于y的方程有非负整数解,且关于x的不等式组的解集为x≥1,则所有符合条件的整数a的和为( )A.﹣5 B.﹣8 C.﹣9 D.﹣12解:,解得:,∵关于y的方程有非负整数解,∴,解得:a≥﹣5,且为整数,关于x的不等式组整理得:,∵不等式组的解集为x≥1,∴a+4≤1,解得:a≤﹣3,∴﹣5≤a≤﹣3且为整数,∴a=﹣5,﹣3,于是符合条件的所有整数a的值之和为:﹣5﹣3=﹣8.故选:B.二.填空题(共10小题,满分20分,每小题2分)11.(2分)(2023秋•惠州期末)不等式组:的解集是 .解:,解不等式①,得x,解不等式②,得x<2,故不等式组的解集为.故答案为:.12.(2分)(2023春•集美区校级期中)若不等式(a﹣1)x>1﹣a的解集是x<﹣1,则a的取值范围是 a<1 .解:两边同时除以(a﹣1)得,x<﹣1,可见,a﹣1<0,解得a<1.故答案为a<1.13.(2分)(2023秋•海曙区期中)不等式组的解集为x>3,则k的取值范围为 k≤2 .解:由3x﹣9>0得:x>3,由x>k+1且不等式组的解集为x>3,知k+1≤3,解得k≤2,故答案为:k≤2.14.(2分)(2023春•富锦市校级期末)已知关于x的不等式组的所有整数解的和为﹣9,m的取值范围是 3≤m<6或﹣6≤m<﹣3 .解:解不等式3x+m<0,得:x<﹣,∵x>﹣5,∴不等式组的解集为﹣5<x<﹣,∵不等式的所有整数解的和为﹣9,∴不等式组的整数解为﹣4、﹣3、﹣2或﹣4、﹣3、﹣2,﹣1,0,1,则﹣2<﹣≤﹣1或1<﹣≤2,解得3≤m<6或﹣6≤m<﹣3,故答案为:3≤m<6或﹣6≤m<﹣3.15.(2分)(2023秋•新田县期末)关于x的不等式组恰有3个整数解,则a的取值范围是 2≤a<3 .解:,解①得:x>a﹣2,解②得:x≤3.∵不等式组恰有3个整数解,∴不等式组的整数解是:1,2,3.∴0≤a﹣2<1,∴2≤a<3.故答案为:2≤a<3.16.(2分)(2023秋•鄞州区期中)若不等式(a﹣1)x<a﹣1的解集是x>1,则a的取值范围是 a<1 .解:∵不等式(a﹣1)x<a﹣1的解集是x>1,∴a﹣1<0,解得a<1.故答案为:a<1.17.(2分)(2023春•渝中区校级期末)关于x的不等式组的解集为x≥3,且关于x的一次方程5x﹣a=x+3有非负整数解,则所有满足条件的整数a的和为 ﹣2 .解:将一元一次不等式组整理得到:,∵不等式组的解集为x≥3,∴a﹣2<3,∴a<5;解关于x的一次方程5x﹣a=x+3得x=.∵x有非负整数解,∴≥0,解得:a≥﹣3,∴﹣3≤a<5,∴满足条件的整数a为:﹣3,1,∴所有满足条件的整数a的和为:﹣3+1=﹣2.故答案为:﹣2.18.(2分)(2023春•重庆期中)若关于x的一元一次方程有正整数解,且使关于x的不等式组至少有4个整数解,求出满足条件的整数a的所有值的积为 15 .解:解不等式2x﹣a≥0,得x≥,解不等式,得x<8,∵不等式组至少有4个整数解,∴≤4,解得a≤8,解关于x的一元一次方程,得x=,∵方程有正整数解,∴>0,则a>0,∴0<a≤8,其中能使为正整数的a值有1,3,5,其积为1×3×5=15.故答案为:15.19.(2分)(2022春•渝中区校级月考)清明将至,前去扫墓的人逐渐增多.某花店购进白菊,白百合,马蹄莲共计m捆.白菊每捆20支,白百合每捆12支,马蹄莲每捆10支.现取出白菊的,白百合的,马蹄莲的,全部用于扎成A、B两款花束销售.其中A款花束白菊2支,白百合3支,马蹄莲1支,B款花束白菊5支,马蹄莲2支.如此取出后剩下的白百合支数不多于马蹄莲支数,则购进的白菊捆数与白百合捆数之比至少为 3:5 .解:设购进白菊有x捆,白百何有y捆,则马蹄莲有(m﹣x﹣y)捆,∵白菊每捆20支,白百合每捆12支,马蹄莲每捆10支,∴白菊有20x支,白百合有12y支,马蹄莲有10(m﹣x﹣y)支,∵现取出白菊的,白百合的,马蹄莲的,全部用于扎成A、B两款花束销售,∴取出的白菊有10x支,白百合有4y支,马蹄莲有(m﹣x﹣y)支,设A款花束有a束,B款花束有b束,根据A款花束白菊2支,白百合3支,马蹄莲1支,B款花束白菊5支,马蹄莲2支可列方程组得:,由②得:a= ④,把④代入①得:b=2x﹣y ⑤,把④和⑤代入③得:m=,∵取出后剩下的白百合支数不多于马蹄莲支数,∴12y﹣4y≤10(m﹣x﹣y)﹣(m﹣x﹣y),即8y≤(﹣x﹣y),整理得:5x≥3y,∴,故答案为:3:5.20.(2分)(2022春•梁园区期末)对于x,符号[x]表示不大于x的最大整数.如:[3.14]=3,[﹣7.59]=﹣8,则满足关系式的x的整数值有 3 个.解:由题意得4≤<5,解得:7≤x<,其整数解为7、8、9共3个.故答案为:3.三.解答题(共8小题,满分60分)21.(6分)(2023秋•桐乡市期末)解不等式,并把解在数轴上表示出来.解:,3(﹣3+x)≤2(2x﹣4),﹣9+3x≤4x﹣8,3x﹣4x≤9﹣8,﹣x≤1,x≥﹣1.将不等式的解集表示在数轴上如下:22.(6分)(2023秋•钢城区期末)解不等式组:,并求出它的非负整数解.解:由①得:x<2,由②得:x≥﹣1,∴不等式组的解集为﹣1≤x<2,则不等式组的非负整数解为0,1.23.(8分)(2023秋•邵阳期末)已知关于x的不等式组;(1)若该不等式组有且只有三个整数解,求a的取值范围;(2)若该不等式组有解,且它的解集中的任何一个值均不在x≥5的范围内,求a的取值范围.解:(1),解不等式①,得:x>2,解不等式②,得:x<7﹣a,∴不等式组的解集为2<x<7﹣a,又∵不等式组有且只有三个整数解,∴5<7﹣a≤6,解得:1≤a<2;(2)由(1)可得,不等式组的解集为2<x<7﹣a,∵不等式组有解,∴7﹣a>2,解得:a<5,又∵它的解集中的任何一个值均不在x≥5的范围内,∴7﹣a≤5,解得:a≥2,∴a的取值范围2≤a<5.24.(8分)(2023春•大竹县校级期末)我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<﹣2.5>=﹣2.根据上述规定,解决下列问题:(1)[﹣4.5]= ﹣5 ,<3.01>= 4 ;(2)若x为整数,且[x]+<x>=2017,求x的值;(3)若x、y满足方程组,求x、y的取值范围.解:(1)由题可得[﹣4.5]=﹣5,<3.01>=4,故答案为:﹣5,4;(2)∵[x]≤x,且x为整数,∴[x]=x,∵<x>>x,且x为整数,∴<x>=x+1,∵[x]+<x>=2017,∴x+(x+1)=2017,解得x=1008;(3)解原方程组,得,又∵[x]表示不大于x的最大整数,<x>表示大于x的最小整数,∴﹣1≤x<0,2≤y<3.25.(8分)(2024•邵阳模拟)某商场同时采购了A,B两种品牌的运动装,第一次采购A品牌运动装10件,B品牌运动装30件,采购费用为8600元;第二次只采购了B品牌运动装50件,采购费用为11000元.(1)求A,B两种品牌运动装的采购单价分别为多少元每件?(2)商家通过一段时间的营销后发现,B品牌运动装的销售明显比A品牌好,商家决定采购一批运动装,要求:①采购B品牌运动装的数量是A品牌运动装的2倍多10件,且A品牌的采购数量不低于18件;②采购两种品牌运动装的总费用不超过15000元,请问该商家有哪几种采购方案?解:(1)设A品牌运动装的采购单价是x元/件,B品牌运动装的采购单价是y元/件,根据题意得:,解得:.答:A品牌运动装的采购单价是200元/件,B品牌运动装的采购单价是220元/件;(2)设该商家采购A品牌运动装m件,则采购B品牌运动装(2m+10)件,根据题意得:,解得:18≤m≤20,又∵m为正整数,∴m可以为18,19,20,∴该商家共有3种采购方案,方案1:采购A品牌运动装18件,B品牌运动装46件;方案2:采购A品牌运动装19件,B品牌运动装48件;方案3:采购A品牌运动装20件,B品牌运动装50件.26.(8分)(2023•曲靖一模)2022年1月7日,《云南省全民健身实施计划(2021﹣2025年)》新闻发布会顺利举行.会议上就“十四五”时期深化体育改革,推进新时代全民健身高质量发展作了全面部署和安排.其中,“强化供给,补齐全民健身设施建设短板”是《云南省全民健身实施计划(2021﹣2025年)》的主要任务之一.春城小区计划购买10台健身器材供小区居民锻炼使用,了解到购买1台B型健身器材比1台A型健身器材贵200元,购买2台A型健身器材和5台B型健身器材共花8000元.(1)A型健身器材和B型健身器材的单价是多少钱?(2)春城小区计划购买B型健身器材的数量不超过A型健身器材的数量的2倍,购买资金不低于10800元,请问共有哪几种购买方案,哪一种方案最省钱.解:(1)设A型健身器材的单价是x元,B型健身器材的单价是y元,依题意得:,解得:.答:A型健身器材的单价是1000元,B型健身器材的单价是1200元.(2)设购买m台A型健身器材,则购买(10﹣m)台B型健身器材,依题意得:,解得:≤m≤6.又∵m为整数,∴m可以为4,5,6,∴共有3种购买方案,方案1:购买4台A型健身器材,6台B型健身器材,所需购买资金为1000×4+1200×6=11200(元);方案2:购买5台A型健身器材,5台B型健身器材,所需购买资金为1000×5+1200×5=11000(元);方案3:购买6台A型健身器材,4台B型健身器材,所需购买资金为1000×6+1200×4=10800(元).∵11200>11000>10800,∴最省钱的购物方案为:购买6台A型健身器材,4台B型健身器材.27.(8分)(2023•金凤区校级二模)围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有4000多年的历史,中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为活跃学生课余生活,欲购买一批象棋和围棋,已知购买3副象棋和1副围棋共需125元,购买2副象棋和3副围棋共需165元.(1)求每副象棋和围棋的价格;(2)若学校准备购买象棋和围棋总共100副,且总费用不超过3200元,则最多能购买多少副围棋?解:(1)设每副象棋的价格为x元,每副围棋的价格为y元.依题意得,解得.答:每副象棋的价格为30元,每副围棋的价格为35元.(2)设购买m副围棋,则购买(100﹣m)副象棋.依题意得:30(100﹣m)+35m≤3200,解得m≤40.答:最多能购买40副围棋.28.(8分)(2022秋•婺城区期末)为更好地推进生活垃圾分类工作,改善城市生态环境,某小区准备购买A、B两种型号的垃圾箱,通过对市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需390元,购买2个A型垃圾箱比购买1个B型垃圾箱少用20元.(1)求每个A型垃圾箱和每个B型垃圾箱分别多少元?(2)该小区计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个,且A型号垃圾箱个数不多于B型垃圾箱个数的3倍,则该小区购买A、B两种型号垃圾箱的方案有哪些?解:(1)设每个A型垃圾箱x元,每个B型垃圾箱y元.依题意,得:,解得:.答:每个A型垃圾箱50元,每个B型垃圾箱120元;(2)设购买m个B型垃圾箱,则购买(20﹣m)个A型垃圾箱.依题意,得:,解得:5≤m≤.又m为整数,m可以为5,6,7,∴有3种购买方案:方案1:购买15个A型垃圾箱,购买5个B型垃圾箱;方案2:购买14个A型垃圾箱,购买6个B型垃圾箱;方案3:购买13个A型垃圾箱,购买7个B型垃圾箱
相关资料
更多









