2023-2024学年福建省泉州市德化二中八年级（上）第一次月考数学试卷（含解析）

这是一份2023-2024学年福建省泉州市德化二中八年级（上）第一次月考数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.在下列各式中正确的是( )
A. (−2)2=−2B. ± 9=3C. 22=2D. 16=8
2. 81的平方根是( )
A. ±3B. 3C. ±9D. 9
3.下列运算正确的是( )
A. a+a+a=a3B. (2a)3=6a3C. a⋅a⋅a=3aD. a8÷a2=a6
4.下列算式中结果等于x9的是( )
A. (−x)2⋅(−x)7B. (−x2)⋅(−x)7C. (−x)2⋅(−x7)D. x2⋅(−x)7
5.要说明命题“若a>b，则a2>b2”是假命题，下列a，b的值能作为反例的是( )
A. a=3，b=2B. a=−1，b=−2
C. a=−2，b=−1D. a=2，b=−1
6.下列命题是假命题的是( )
A. 在同一平面内，过一点有且只有一条直线与已知直线垂直
B. 负数没有立方根
C. 在同一平面内，若a⊥b，b⊥c，则a/​/c
D. 同旁内角互补，两直线平行
7.如图，已知MB=ND，∠MBA=∠NDC，下列条件不能判定△ABM≌△CDN的是( )
A. ∠M=∠N
B. AM/​/CN
C. AC=BD
D. AM=CN
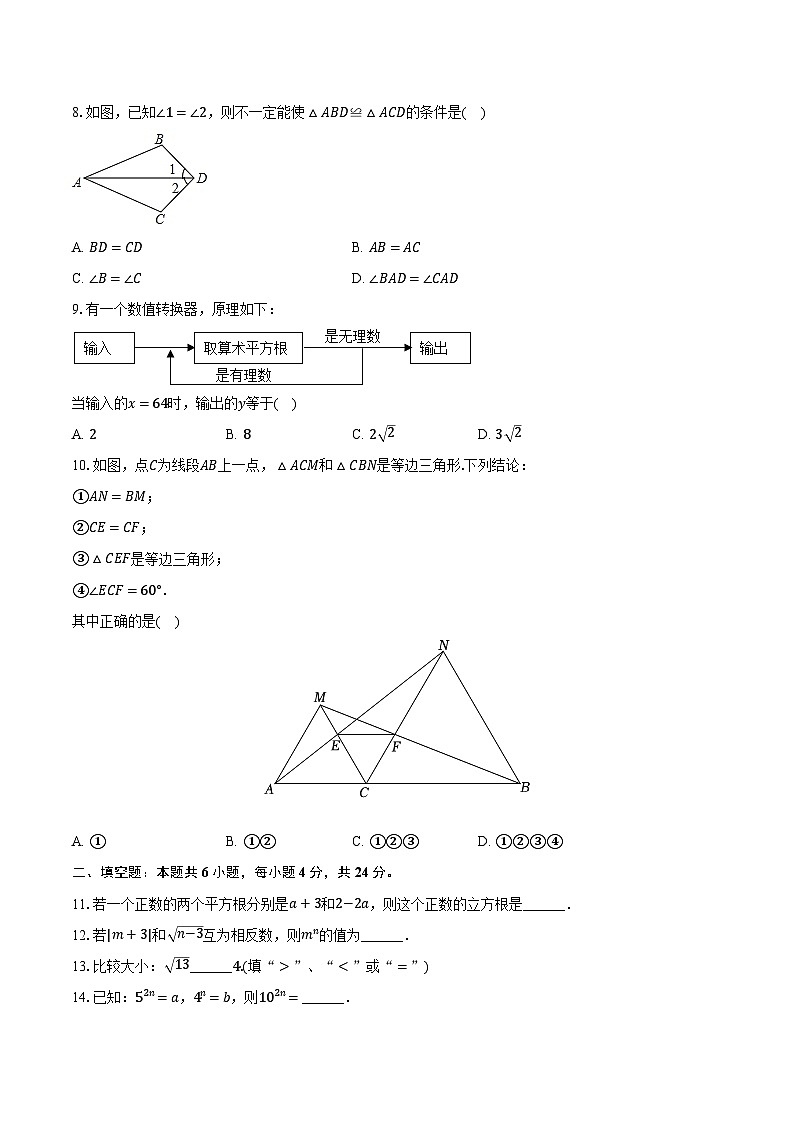
8.如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是( )
A. BD=CDB. AB=AC
C. ∠B=∠CD. ∠BAD=∠CAD
9.有一个数值转换器，原理如下：

当输入的x=64时，输出的y等于( )
A. 2B. 8C. 2 2D. 3 2
10.如图，点C为线段AB上一点，△ACM和△CBN是等边三角形.下列结论：
①AN=BM；
②CE=CF；
③△CEF是等边三角形；
④∠ECF=60°．
其中正确的是( )
A. ①B. ①②C. ①②③D. ①②③④
二、填空题：本题共6小题，每小题4分，共24分。
11.若一个正数的两个平方根分别是a+3和2−2a，则这个正数的立方根是______．
12.若|m+3|和 n−3互为相反数，则mn的值为______．
13.比较大小： 13______4.(填“>”、“<”或“=”)
14.已知：52n=a，4n=b，则102n=______．
15.如图，已知在△ABC中，∠BAC=90°，AB=AC，AE是过点A的直线，BD⊥AE，CE⊥AE，垂足分别是D、E，若CE=3，BD=7，则DE= ______．
16.如图，已知长方形ABCD的边长AB=20cm，BC=16cm，点E在边AB上，AE=6cm，如果点P从点B出发在线段BC上向点C运动，同时，点Q在线段DC上从点D向点C运动，已知点P的运动速度是2cm/s.则经过______s，△BPE与△CQP全等．
三、计算题：本大题共1小题，共8分。
17.计算：|4− 7|+3−27+ 7+ 25
四、解答题：本题共8小题，共68分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题8分)
如图所示，AC=AE，∠1=∠2，AB=AD.求证：BC=DE．
19.(本小题8分)
已知5a+2的立方根是3，3a+b−1的算术平方根是4，c是 11的整数部分．
(1)求a，b，c的值；
(2)求3a−b+c的平方根．
20.(本小题8分)
如图，B、E、F、C在同一条直线上，AF⊥BC于点F，DE⊥BC于点E，AB=DC，BE=CF，求证：AB/​/CD．
21.(本小题8分)
如图，一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B，点A表示− 2，设点B所表示的数为m．
(1)求|m+1|+|m−1|的值；
(2)在数轴上还有C、D两点分别表示实数c和d，且有|2c+6|与 d−4互为相反数，求2c+3d的平方根．
22.(本小题8分)
阅读下列信息材料：
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π、 2等，而常用的“…”或者“≈”的表示方法都不够百分百准确；
信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.5−2得来的；
信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如2< 5<3，是因为 4< 5< 9；
根据上述信息，回答下列问题：
(1) 13的整数部分是______，小数部分是______；
(2)若21(3)10+ 3也是夹在相邻两个整数之间的，可以表示为a<10+ 3(4)若 30−3=x+y，其中x是整数，且023.(本小题10分)
如图，已知△ABC中，∠B=∠C，AB=8厘米，BC=6厘米，点D为AB的中点．如果点P在线段BC上以每秒2厘米的速度由B点向C点运动，同时，点Q在线段CA上以每秒a厘米的速度由C点向A点运动，设运动时间为t(秒)(0≤t≤3)．
(1)用含t的代数式表示PC的长度；
(2)若点P、Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
(3)若点P、Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等？
24.(本小题8分)
如图，在△ACB和△DCE中，AC=BC，CD=CE，∠ACB=∠DCE=90°，连接AE、BD交于点O，AE与DC交于点M，BD与AC交于点N.试判断AE、BD之间的关系，并说明理由．
25.(本小题10分)
如图，Rt△ACB中，∠ACB=90°，AC=BC，E点为射线CB上一动点，连接AE，作AF⊥AE且AF=AE．
(1)如图1，过F点作FD⊥AC交AC于D点，求证：EC+CD=DF；
(2)如图2，连接BF交AC于G点，若AGCG=3，求证：E点为BC中点；
(3)当E点在射线CB上，连接BF与直线AC交于G点，若BCBE=43，则AGCG=______(直接写出结果)
答案和解析
1.【答案】C
【解析】解：A、 (−2)2= 22=2，故错误；
B、± 9=±3，故错误；
C、正确；
D、 16=4，故错误；
故选：C．
关键算术平方根的定义，即可解答．
本题考查了算术平方根，解决本题的关键是熟记算术平方根的定义．
2.【答案】A
【解析】解： 81=9，9的平方根是±3．
故选：A．
根据算术平方根、平方根的定义即可求解．
本题考查了算术平方根、平方根的定义，掌握算术平方根、平方根的定义是解题的关键．
3.【答案】D
【解析】解：A、a+a+a=3a，故此选项错误；
B、(2a)3=8a3，故此选项错误；
C、a⋅a⋅a=a3，故此选项错误；
D、a8÷a2=a6，正确．
故选：D．
直接利用同底数幂的乘除运算法则以及积的乘方运算法则、合并同类项法则分别计算得出答案．
此题主要考查了同底数幂的乘除运算以及积的乘方运算、合并同类项，正确掌握相关运算法则是解题关键．
4.【答案】B
【解析】解：A、(−x)2⋅(−x)7=(−x)9=−x9，故本选项错误；
B、(−x2)⋅(−x)7=−x2⋅(−x7)=x9，故本选项正确；
C、(−x)2⋅(−x7)=x2⋅(−x7)=−x9，故本选项错误；
D、x2⋅(−x)7=−x9，故本选项错误．
故选B．
根据同底数幂的乘法的运算法则求解即可求得答案．注意排除法在解选择题中的应用．
此题考查了同底数幂的乘法的性质．此题难度不大，注意掌握符号的变化是解此题的关键．
5.【答案】B
【解析】解：A、a=3，b=2满足a>b，a2>b2，不能作为反例，故不符合题意；
B、a=−1，b=−2满足a>b，但a2C、a=−2，b=−1不满足a>b，不能作为反例，故不符合题意；
D、a=2，b=−1满足a>b，a2>b2，不能作为反例，故不符合题意；
故选：B．
作为反例，要满足条件但不能得到结论，然后根据这个要求对各选项进行判断．
本题考查了命题和反例，熟练掌握反例的意义是解题的关键．
6.【答案】B
【解析】解：A、在同一平面内，过一点有且只有一条直线与已知直线垂直，是真命题；
B、负数有立方根，原命题是假命题；
C、在同一平面内，若a⊥b，b⊥c，则a/​/c，是真命题；
D、同旁内角互补，两直线平行，是真命题；
故选：B．
根据垂直的定义、立方根及平行线的判定与性质判断即可．
本题考查了命题与定理的知识，解题的关键是了解垂直的定义、立方根及平行线的判定与性质等知识，难度不大．
7.【答案】D
【解析】解：A、∠M=∠N，符合ASA，能判定△ABM≌△CDN，故A选项不符合题意；
B、AM/​/CN，得出∠MAB=∠NCD，符合AAS，能判定△ABM≌△CDN，故B选项不符合题意．
C、根据条件MB=ND∠MBA=∠NDC，AB=CD，符合SAS，能判定△ABM≌△CDN，故C选项不符合题意；
D、MB=ND，∠MBA=∠NDC，不能判定△ABM≌△CDN，故D选项符合题意；
故选：D．
根据普通三角形全等的判定定理，有AAS、SSS、ASA、SAS四种．逐条验证即可．
本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，本题是一道较为简单的题目．
8.【答案】B
【解析】【分析】
本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL.注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．利用全等三角形判定定理ASA，SAS，AAS对各个选项逐一分析即可得出答案．
【解答】
解：A、∵∠1=∠2，AD为公共边，若BD=CD，则△ABD≌△ACD(SAS)；
B、∵∠1=∠2，AD为公共边，若AB=AC，不符合全等三角形判定定理，不能判定△ABD≌△ACD；
C、∵∠1=∠2，AD为公共边，若∠B=∠C，则△ABD≌△ACD(AAS)；
D、∵∠1=∠2，AD为公共边，若∠BAD=∠CAD，则△ABD≌△ACD(ASA)；
故选B．
9.【答案】C
【解析】解：当x=64时， 64=8(有理数)，
将x=8代入得： 8=2 2(无理数)．
故选：C．
将x=64代入程序进行计算即可．
本题主要考查的是算术平方根的定义、无理数的定义，依据程序进行计算是解题的关键．
10.【答案】D
【解析】解：(1)∵△ACM，△CBN是等边三角形，
∴AC=MC，BC=NC，∠ACM=60°=∠NCB=60°，
∴∠ACM+∠MCN=∠NCB+∠MCN，即∠ACN=∠MCB
在△CAN和△MCB中，
AC=MC∠ACN=∠MCBNC=BC，
∴△CAN≌△CMB(SAS)，
∴AN=BM，①正确；
∵△CAN≌△CMB，
∴∠CAN=∠CMB，
又∵∠ECF=180°−∠ACM−∠NCB=180°−60°−60°=60°，
∴∠ECF=∠ACE，
在△CAE和△CMF中，
∠CAE=∠CMFCA=CM∠ACE=∠ECF，
∴△CAE≌△CMF(ASA)，
∴CE=CF，
∴△CEF为等腰三角形，
又∵∠ECF=60°，
∴△CEF为等边三角形，所以①②③④正确，
故选：D．
由等边三角形可得其对应线段相等，对应角相等，进而可由SAS得到△CAN≌△CMB，再由△CAN≌△CMB可得∠CAN=∠CMB，进而得出∠MCF=∠ACE，由ASA得出△CAE≌△CMF，即CE=CF，又ECF=60°，所以△CEF为等边三角形结论得以验证．
本题考查了全等三角形的性质和判定及等边三角形的判定，解答本题的关键是掌握全等三角形的判定定理：SAS，ASA，AAS，SSS，HL，全等三角形的对应边相等，对应角相等．
11.【答案】4
【解析】解：根据题意得：a+3+2−2a=0，
解得：a=5，
则这个正数为(5+3)2=64，
则这个正数的立方根是4．
故答案为：4．
根据一个正数的平方根有2个，且互为相反数求出a的值，即可确定出正数的立方根．
此题考查了立方根，以及平方根，熟练掌握各自的定义是解本题的关键．
12.【答案】−27
【解析】解：∵|m+3|和 n−3互为相反数，
∴|m+3|+ n−3=0，
∵|m+3|≥0， n−3≥0，
∴m+3=0，n−3=0，
解得：m=−3，n=3，
∴mn=(−3)3=−27，
故答案为：−27．
根据相反数的定义得|m+3|+ n−3=0，从而由|m+3|≥0， n−3≥0，可得m+3=0，n−3=0，解出m、n的值，代入所求式子就可以求解．
本题主要考查了非负数的性质和有理数的乘方等知识点，理解并能应用几个非负数的和为0，则这几个数都为0是解题的关键．
13.【答案】<
【解析】解：∵ 16=4，
∴ 13< 16=4，
∴ 13<4．
故答案为：<．
直接利用实数比较大小的方法分析得出答案．
此题主要考查了实数比较大小，正确掌握算术平方根的性质是解题关键．
14.【答案】ab
【解析】【分析】
利用幂的乘方运算法则和积的乘方运算法则将已知和原式变形，然后整体代入求值即可．
【解答】
解：因为52n=a，4n=b，
所以52n=a，22n=b，
所以102n=(5×2)2n=52n×22n=ab．
故答案为：ab．
【点评】
本题主要考查了幂的乘方和积的乘方运算，正确将式子变形是解题关键．
15.【答案】4
【解析】解：∵BD⊥AE，CE⊥AE，
∴∠BDA=∠AEC=90°
∵∠BAC=90°，
∴∠BAD=∠BAC−∠CAE=90°−∠CAE，
在△AEC中，∠ACE=∠AEC−∠CAE=90°−∠CAE，
∴∠BAD=∠ACE，
在△ADB和△CEA中，AB=AC
∴△ADB≌△CEA(AAS)，
∴CE=AD，BD=AE，
∴DE=AE−AD=BD−CE=7−3=4．
故填空答案：4．
只要利用已知条件证明△ADB≌△CEA即可求出DE的长．
此题考查了全等三角形的判定与性质，也利用等量代换的数学思想．
16.【答案】1或4
【解析】解：分两种情况：
①当EB=PC，BP=QC时，△BPE≌△CQP，
∵AB=20cm，AE=6cm，
∴EB=14cm，
∴PC=14cm，
∵BC=16cm，
∴BP=2cm，
∵点P从点B出发在线段BC上以2cm/s的速度向点C运动，
∴t=2÷2=1(s)；
②当BP=CP，BE=QC时，△BEP≌△CQP，
由题意得：2t=16−2t，
解得：t=4(s)，
故答案为：1或4．
设P运动的时间为t s，由条件分两种情况，当△BPE≌△CQP时，则有BE=PC，由条件可得到关于t的方程，当△BPE≌△CPQ，则有BP=PC，同样可得出t的方程，可求出t的值．
本题主要考查全等三角形的判定，矩形的性质，由条件分两种情况得到关于t的方程是解题的关键．
17.【答案】解：原式=4− 7−3+ 7+5=6．
【解析】原式利用绝对值的代数意义，立方根、平方根定义计算即可求出值．
此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
18.【答案】证明：∵∠1=∠2，
∴∠CAB=∠EAD
在△CAB和△EAD中AC=AE∠CAB=∠EADAB=AD，
∴△CAB≌△EAD(SAS)
∴BC=DE
【解析】先判断出∠CAB=∠EAD，进而判断出△CAB≌△EAD即可得出结论．
此题是三角形全等的判定和性质，解本题的关键是判断出∠CAB=∠EAD．
19.【答案】解：(1)因为5a+2的立方根是3，3a+b−1的算术平方根是4，
所以5a+2=27，3a+b−1=16，
所以a=5，b=2；
因为3< 11<4，c是 11的整数部分，
所以c=3；
(2)由(1)知，a=5，b=2，c=3，则3a−b+c=15−2+3=16，16的平方根是±4．
【解析】点拨
(1)利用立方根的定义、算术平方根的定义、无理数的估算方法，求出a、b、c的值；
(2)将a、b、c的值代入代数式求出值后，进一步求得平方根即可．
此题考查立方根的定义、算术平方根的定义、无理数的估算方法、平方根的定义、代数式求值等知识点，读懂题意，掌握解答顺序，正确计算即可．
20.【答案】证明：∵AF⊥BC，DE⊥BC，
∴∠AFB=∠DEC=90°，
∵BE=CF，
∴BE+EF=CF+EF，
∴BF=CE，在Rt△AFB和Rt△DEC中，BF=CEAB=DC，
∴Rt△AFB≌Rt△DEC(HL)，
∴∠B=∠C，
∴AB/​/CD．
【解析】由已知得出∠AFB=∠DEC=90°，推出BF=CE，由HL证得Rt△AFB≌Rt△DEC得出∠B=∠C，即可得出结论．
本题考查了全等三角形的判定与性质、平行线的判定等知识，熟练掌握全等三角形的判定是解题的关键．
21.【答案】解：(1)∵AB=2，
∴m−(− 2)=2，
∴m=2− 2，
∴|m+1|+|m−1|
=|2− 2+1|+|2− 2−1|
=|3− 2|+|1− 2|
=3− 2+ 2−1
=2；
(2)∵|2c+6|与 d−4互为相反数，
∴|2c+6|+ d−4=0，
∵|2c+6|≥0， d−4≥0，
∴2c+6=0，d−4=0，
∴c=−3，d=4，
∴2c+3d=2×(−3)+3×4=6，
∴2c+3d的平方根是± 6．
【解析】(1)利用两点间的距离公式计算即可；
(2)利用非负数的性质，得到c，d的值，代入求值即可．
本题考查了两点间的距离公式、平方根，解题的关键是熟练掌握两点的距离公式，注意平方根有两个．
22.【答案】3 13−3 21 a−21 23
【解析】解：(1)∵ 9< 13< 16，
∴3< 13<4，
∴ 13的整数部分是3，小数部分是 13−3，
故答案为：3， 13−3．
(2)显然a的整数部分为21，小数部分为a减去它的整数部分，即为a−21，
故答案为：21，a−21．
(3)∵ 1< 3< 4，
∴1< 3<2，
∴11<10+ 3<12，
∴a=11，b=12，
∴a+b=11+12=23，
故答案为：23．
(4)∵ 25< 30< 36，
∴5< 30<6，
∴2< 30−3<3，
又∵x是整数，且0∴x=2，y=( 30−3)−2= 30−5，
∴x−y=2−( 30−5)=7− 30，
∴x−y的相反数是 30−7．
(1)根据信息3可得： 9< 13< 16，再根据信息2即可得到答案；
(2)根据信息2即可得到答案；
(3)根据信息3可得1< 3<2，从而得到11<10+ 3<12，即可得到答案．
(4)根据信息(3)可得 25< 30< 36，即5< 30<6，从而得到2< 30−3<3，再根据x是整数，且0本题考查了无理数的估值方法，理解题中所给信息并能灵活运用是解决此题的关键．
23.【答案】解：(1)BP=2t，则PC=BC−BP=6−2t；
(2)△BPD和△CQP全等
理由：∵t=1秒∴BP=CQ=2×1=2厘米，
∴CP=BC−BP=6−2=4厘米，
∵AB=8厘米，点D为AB的中点，
∴BD=4厘米．
∴PC=BD，
在△BPD和△CQP中，
BD=PC∠B=∠CBP=CQ，
∴△BPD≌△CQP(SAS)；
(3)∵点P、Q的运动速度不相等，
∴BP≠CQ
又∵△BPD≌△CPQ，∠B=∠C，
∴BP=PC=3cm，CQ=BD=4cm，
∴点P，点Q运动的时间t=BP2=32秒，
∴a=CQt=432=83厘米/秒．
【解析】此题考查了全等三角形的判定，主要运用了路程=速度×时间的公式，要求熟练运用全等三角形的判定和性质．
(1)先表示出BP，根据PC=BC−BP，可得出答案；
(2)根据时间和速度分别求得两个三角形中的边的长，根据SAS判定两个三角形全等．
(3)根据全等三角形应满足的条件探求边之间的关系，再根据路程=速度×时间公式，先求得点P运动的时间，再求得点Q的运动速度；
24.【答案】解：AE=BD且AE⊥BD.理由如下：
∵∠ACB=∠DCE，
∴∠ACB+∠DCA=∠DCE+∠DCA，
即∠DCB=∠ACE，
∵AC=BC，CD=CE，
∴△ACE≌△BCD(SAS)，
∴AE=BD，∠CEA=∠BDC，
∵∠CME=∠DMO，
∴∠DOM=∠ECM=90°，
∴AE⊥BD，
∴AE=BD且AE⊥BD．
【解析】此题考查了全等三角形的性质及其判定，找到全等三角形，利用全等三角形的性质推出角之间的关系为解题关键．根据∠ACB=∠DCE，可得∠DCB=∠ACE，已知AC=BC，CD=CE，可得△ACE≌△BCD，则AE=BD，∠CEA=∠BDC，AE⊥BD，即AE=BD且AE⊥BD．
25.【答案】113或53
【解析】证明：(1)如图1，∵∠FAD+∠CAE=90°，∠FAD+∠F=90°，
∴∠CAE=∠AFD，
在△ADF和△ECA中，
∠ADF=∠ECA∠DFA=∠CAEAF=AE，
∴△ADF≌△ECA(AAS)，
∴AD=EC，FD=AC，
∴CE+CD=AD+CD=AC=FD，即EC+CD=DF；
证明：(2)如图2，过F点作FD⊥AC交AC于D点，
∵△ADF≌△ECA，
∴FD=AC=BC，
在△FDG和△BCG中，
∠FGD=∠CGB∠FDG=∠C=90°FD=BC，
∴△FDG≌△BCG(AAS)，
∴GD=CG，
∵AGCG=3，
∴ADCG=2，
∴ADAC=12，
∵AD=CE，AC=BC
∴CEBC=12，
∴E点为BC中点；
(3)过F作FD⊥AG的延长线交于点D，如图3，
∵BCBE=43，BC=AC，CE=CB+BE，
∴ACCE=47，
由(1)(2)知：△ADF≌△ECA，△GDF≌△GCB，
∴CG=GD，AD=CE，
∴ACAD=47，
∴ACCD=43，
∴AC12AD=83，
∴AGCG=113．
同理，当点E在线段BC上时，AGCG=53．
故答案为：113或53．
(1)通过全等三角形△ADF≌△EDA的对应边相等得到：AD=CD，FD=AC，则利用等量代换和图形中相关线段间的和差关系证得结论；
(2)过F点作FD⊥AC交AC于D点，根据(1)中结论可得FD=AC=BC，即可证明△FGD≌△BCD，可得DG=CG，根据AGCG=3可证ADAC=12，根据AD=CE，AC=BC，即可解题；
(3)过F作FD⊥AG的延长线交于点D，易证ACCE=47，由(1)(2)可知△ADF≌△ECA，△GDF≌△GCB，可得CG=GD，AD=CE，即可求得AGCG的值，即可解题．
本题考查了相似综合题，需要掌握全等三角形的判定，全等三角形对应边相等的性质，本题中求证△ADF≌△ECA、△GDF≌△GCB是解题的关键．