人教版八年级数学下册 专题06特殊平行四边形的两种考法全攻略(原卷版+解析)

这是一份人教版八年级数学下册 专题06特殊平行四边形的两种考法全攻略(原卷版+解析)，共28页。试卷主要包含了最值问题，动点问题等内容，欢迎下载使用。

例1．（将军饮马）如图，在菱形中，，E是边的中点，P是边上一动点，的最小值是，则的最小值为（ ）
A．2B．C．1D．0.5
例2．（中点模型）如图，矩形，点A在x轴正半轴上，点D在y轴正半轴上，当点A在x轴上运动时，点D也随之在y轴上运动，在这个运动过程中，点C到原点O的最大距离为（ ）
A．B．2C．D．
例3．（截补模型）如图，在中，，，点、分别是边、上的动点．且，连接、，则的最小值为______．
例4．（瓜豆模型）如图，平面内三点，，，，，以为对角线作正方形，连接，则的最大值是______．
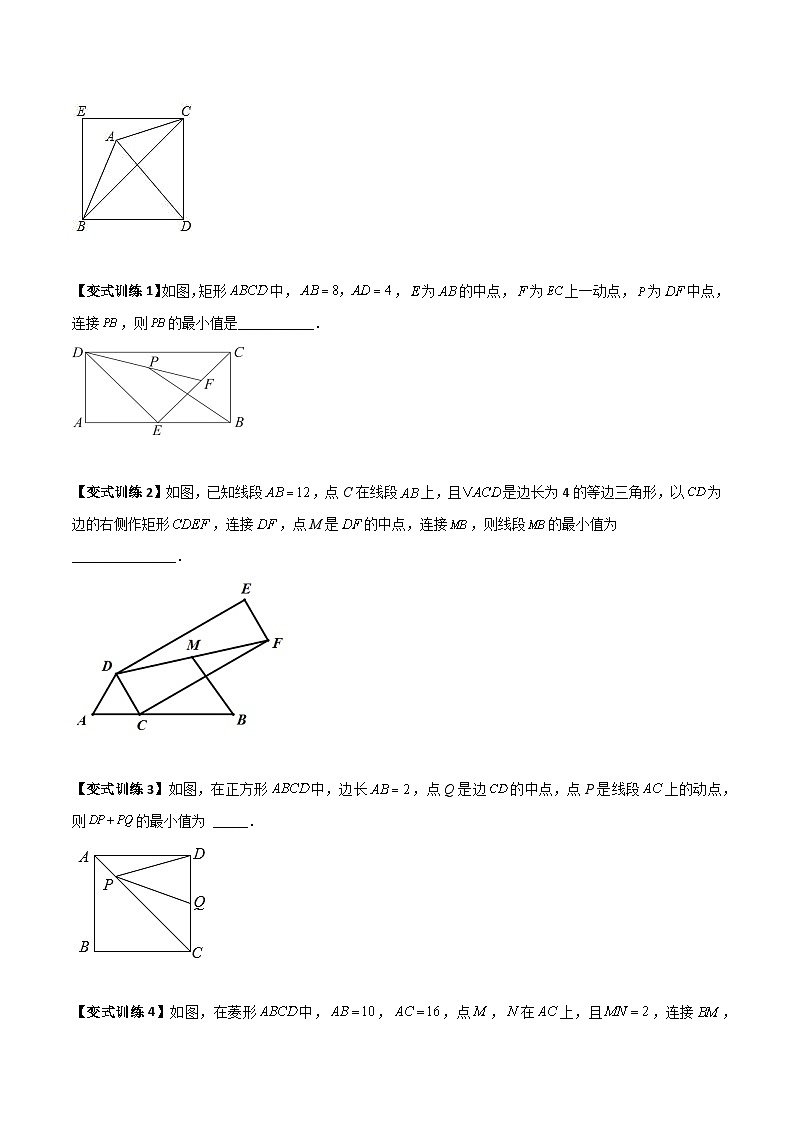
【变式训练1】如图，矩形中，，为的中点，为上一动点，为中点，连接，则的最小值是___________．
【变式训练2】如图，已知线段，点C在线段上，且是边长为4的等边三角形，以为边的右侧作矩形，连接，点M是的中点，连接，则线段的最小值为_______________．
【变式训练3】如图，在正方形中，边长，点Q是边的中点，点P是线段上的动点，则的最小值为 _____．
【变式训练4】如图，在菱形中，，，点，在上，且，连接，，则的最小值为 ______
【变式训练5】如图，在中，，且，，点D是斜边上的一个动点，过点D分别作于点M，于点N，连接，则线段的最小值为_____．
类型二、动点问题
例1．如图，在正方形中，E为的中点，以A为原点，、所在直线为x轴、y轴，建立平面直角坐标系．正方形的边长是方程的根．点P从点B出发，沿向点D运动，同时点Q从点E出发，沿向点C运动，点P的速度是每秒2个单位长度，点Q的速度是每秒1个单位长度．当点P运动到点D时，P、Q两点同时停止运动，设点P运动的时间为t秒，的面积为S．
(1)求点C的坐标；
(2)求S关于t的函数关系式；
(3)当是以为底边的等腰三角形时，直接写出点P的坐标．
例2.如图，在长方形中，，，点为延长线上一点，且，点从点出发，沿———向终点运动．同时点从点出发，沿———向终点运动，它们的速度均为每秒1个单位长度．设的面积为，点运动的时间为秒．
(1)当时， ；当时， ．
(2)当时，用含的代数式表示．直接写出结果并化简．
(3)当点在边上，且为等腰三角形时，直接写出的取值或者范围．
【变式训练1】如图，在中，为锐角，，，．动点从点出发，以每秒2个单位的速度沿运动．同时，动点从点出发，以每秒3个单位的速度沿运动．当其中一个点到达终点时，另一个点也随之停止运动．设点的运动时间为秒．
(1)点在上运动时，_____________；点在上运动时，_____________．（用含的代数式表示）
(2)点在上，时，求的值．
(3)当直线平分的面积时，求的值．
(4)若点的运动速度改变为每秒个单位．当，的某两个顶点与、所围成的四边形为菱形时，直接写出的值．
【变式训练2】如图，长方形中，，，，动点P从点B出发，以每秒的速度沿的方向，向终点D运动；动点Q从点B出发以每秒的速度沿的方向向终点C运动．以为边向右上方作正方形，其中一个动点到达终点时，另一个动点也随之停止运动，设点同时出发，运动时间为t秒．
(1)当时，＝______（用含t的代数式表示）；
(2)当点N落在边上时，求t的值；
(3)当正方形与长方形的重叠部分为四边形时，求重叠部分的面积S（用含t的代数式表示）；
(4)请直接写出当t满足什么条件时，正方形与长方形的重叠部分为三角形．
【变式训练3】已知在矩形ABCD中，AB＝4，AD＝9，点M在AD上，且AM＝4，动点P从点B出发，以每秒1个单位长度的速度，沿B﹣C﹣D﹣A向终点A运动，运动时间为t秒．
(1)当点P在BC边上时，BP＝ ，CP＝ ．（用含t的代数式表示）
(2)点P在运动过程中，△ABP是直角三角形时，t的取值范围为 ．
(3)点P在运动过程中，△DMP是等腰三角形时，t的值为 ．
(4)连接CM，当点P在线段CM的垂直平分线上时，t的值为 ．
专题06 特殊平行四边形的两种考法全攻略
类型一、最值问题
例1．（将军饮马）如图，在菱形中，，E是边的中点，P是边上一动点，的最小值是，则的最小值为（ ）
A．2B．C．1D．0.5
【答案】D
【详解】解：连接交于P，连接，
由菱形的对角线互相垂直平分，可得关于对称，则，
∴，，
即就是的最小值，
∵，
∴是等边三角形，
∵E是边的中点
∴，
∴（等腰三角形三线合一的性质）
在中，，
∴，
∴．
∴
当时最小
∵
∴
故选：D
例2．（中点模型）如图，矩形，点A在x轴正半轴上，点D在y轴正半轴上，当点A在x轴上运动时，点D也随之在y轴上运动，在这个运动过程中，点C到原点O的最大距离为（ ）
A．B．2C．D．
【答案】A
【详解】如图，取的中点，连接，，
矩形，，，
，，
点是的中点，
，
，
，点是的中点，
，
在中，，
当点在上时，，
的最大值为，
故选：A．
例3．（截补模型）如图，在中，，，点、分别是边、上的动点．且，连接、，则的最小值为______．
【答案】
【详解】解：过B作，在上截取，连接，
∵，，
∴，，
∵，
∴，
∴，
当A、D、F在同一直线上时，的最小值为的长，
延长到G，使，连接，
∴，，
∴四边形为平行四边形，
∵，，
∴四边形为正方形，且边长为2，
∴，，
∴，即的最小值为，
故答案为：．
例4．（瓜豆模型）如图，平面内三点，，，，，以为对角线作正方形，连接，则的最大值是______．
【答案】
【详解】解：如图，将绕点D顺时针旋转得到，连接，
则，
∴是等腰直角三角形，，
∴(舍负)，
∴当的值最大时，的值最大，
∵， ，，
∴，（A、C、M三点共线时取等号）
∴的最大值为，
∴的最大值为．
故答案为：．
【变式训练1】如图，矩形中，，为的中点，为上一动点，为中点，连接，则的最小值是___________．
【答案】
【详解】解：如图：
当点F与点C重合时，点P在处，，
当点F与点E重合时，点P在处，，
∴且．
当点F在上除点C、E的位置处时，有．
由中位线定理可知：且．
∴点P的运动轨迹是线段，
∴当时，取得最小值．
∵矩形中，，为的中点，
∴、、为等腰直角三角形，．
∴，．
∴．
∴．
∴，即，
∴的最小值为的长．
在中，，
∴，
∴的最小值是．
故答案是：．
【变式训练2】如图，已知线段，点C在线段上，且是边长为4的等边三角形，以为边的右侧作矩形，连接，点M是的中点，连接，则线段的最小值为_______________．
【答案】6
【详解】∵为等边三角形，
∴，，
∵四边形是矩形，点M是的中点，∴DM＝CM，
在与中，， ∴，∴，
∵，∴，即直线的位置是固定的，
∴当时，有最小值，此时．
【变式训练3】如图，在正方形中，边长，点Q是边的中点，点P是线段上的动点，则的最小值为 _____．
【答案】
【详解】解：连接，交于点P，连接、．
∵四边形是正方形，∴点B与点D关于对称，
∴，∴．
∵，点Q是边的中点，∴，，
在中，，
∴的最小值为．
故答案为: ．
【变式训练4】如图，在菱形中，，，点，在上，且，连接，，则的最小值为 ______
【答案】
【详解】解：连接，交于点，过作，且，连接．
四边形是平行四边形，
，
，
即的最小值为，
四边形是菱形，，
，
又，
在中，，
，
，
在中，，
，
即的最小值为，
故答案为：．
【变式训练5】如图，在中，，且，，点D是斜边上的一个动点，过点D分别作于点M，于点N，连接，则线段的最小值为_____．
【答案】
【详解】解：连接，
∵，且，，
∴，
∵，，
∴，
∴四边形是矩形，
∴，
∴当时，的值最小，
此时，的面积，
∴，
∴的最小值为；
故答案为：．
类型二、动点问题
例1．如图，在正方形中，E为的中点，以A为原点，、所在直线为x轴、y轴，建立平面直角坐标系．正方形的边长是方程的根．点P从点B出发，沿向点D运动，同时点Q从点E出发，沿向点C运动，点P的速度是每秒2个单位长度，点Q的速度是每秒1个单位长度．当点P运动到点D时，P、Q两点同时停止运动，设点P运动的时间为t秒，的面积为S．
(1)求点C的坐标；
(2)求S关于t的函数关系式；
(3)当是以为底边的等腰三角形时，直接写出点P的坐标．
【答案】(1)
(2)
(3)或
【详解】（1）∵正方形的边长是方程的根，
解方程，
得，
∴正方形的边长为4，
∴，，
∴点C的坐标为；
（2）∵E为的中点，
∴
由题意得：，
分两种情况：
①时，如图
由题意得：，，
∴，
；
②时，如图
由题意得：，，
∴，，，
，
∴
，
∴S关于t的函数关系式为
（3）分两种情况：
①时，如图：
由题意得：，，
∴，，
当时，，
∴，解得(舍去)或2，
∴，
∴当，是以为底边的等腰三角形时，；
②时，如图：
由题意得：，，
∴，
，
，
，
当时，，
∴，解得(舍去)或4，∴，∴；
∴当，是以为底边的等腰三角形时，，
综上所述，当是以为底边的等腰三角形时，点P的坐标为或
例2.如图，在长方形中，，，点为延长线上一点，且，点从点出发，沿———向终点运动．同时点从点出发，沿———向终点运动，它们的速度均为每秒1个单位长度．设的面积为，点运动的时间为秒．
(1)当时， ；当时， ．
(2)当时，用含的代数式表示．直接写出结果并化简．
(3)当点在边上，且为等腰三角形时，直接写出的取值或者范围．
【答案】(1)，
(2)
(3)秒或秒或秒
【详解】（1）解：根据题意，
当时，，，
∴；
当时，，的高为，
∴；
故答案为：，；
（2）解：当时，如图所示，
∵，，
∴；
当时，如图所示，
∵，的高为，∴；
当时，如图所示，
∵，，，，
∴
；
∴；
（3）解：当点在边上，且为等腰三角形时，分三种情况讨论：
①当时，如图所示，
设，则，，∴，
∵，∴，
解得（舍去），，∴；
②当时，如图所示：
设，则，，∴，
∵，∴，解得，∴；
③当时，如图所示：
∴，，，
∴，
，
∴，
解得或（舍去），
∴；
综上所述，的值为秒或秒或秒．
【变式训练1】如图，在中，为锐角，，，．动点从点出发，以每秒2个单位的速度沿运动．同时，动点从点出发，以每秒3个单位的速度沿运动．当其中一个点到达终点时，另一个点也随之停止运动．设点的运动时间为秒．
(1)点在上运动时，_____________；点在上运动时，_____________．（用含的代数式表示）
(2)点在上，时，求的值．
(3)当直线平分的面积时，求的值．
(4)若点的运动速度改变为每秒个单位．当，的某两个顶点与、所围成的四边形为菱形时，直接写出的值．
【答案】(1)；
(2)
(3)或
(4)
【详解】（1）根据题意：
当点在上运动时，，
当点在上运动时，，
故答案为：；
（2）当点在上，时，点在上，且，
∴，
∴，
解得：，
∴的值为：
（3）∵当点依次在、、、上时，
的取值范围依次为：、、、，
当点依次在、、、上时，
的取值范围依次为：、、、，
由于当其中一个点到达终点时，另一个点也随之停止运动．
∴
当，点在上，点在上时，直线平分的面积，
∴，即，
解得：，
当，点在上，点在上时，直线平分的面积，
∴，即，
解得：，
综上所述：当直线平分的面积时，的取值为：或
（4）∵，
∴，
∴点在上，
∴，且，
∴的某两个顶点与、所围成的菱形只能是：，
∴点在边上，，
∵此时：，
∴，
【变式训练2】如图，长方形中，，，，动点P从点B出发，以每秒的速度沿的方向，向终点D运动；动点Q从点B出发以每秒的速度沿的方向向终点C运动．以为边向右上方作正方形，其中一个动点到达终点时，另一个动点也随之停止运动，设点同时出发，运动时间为t秒．
(1)当时，＝______（用含t的代数式表示）；
(2)当点N落在边上时，求t的值；
(3)当正方形与长方形的重叠部分为四边形时，求重叠部分的面积S（用含t的代数式表示）；
(4)请直接写出当t满足什么条件时，正方形与长方形的重叠部分为三角形．
【答案】(1)
(2)
(3)当时，；当时，
(4)当或时，正方形与长方形的重叠部分为三角形
【详解】（1）当时，；
故答案为：；
（2）如图1，
∵，
∴，
∵四边形是正方形，
∴，
∴，
∵，
∴，
∵，
∴，
∴ ，
∴，
∴；
（3）由（2）知，时，正方形在长方形的内部，
∴，正方形与长方形的重叠部分为四边形，
∴；
如图2，当P点运动到A点处，，此时正方形与长方形的重叠部分为三角形，
如图3，当M点运动到D点处时，
∵，
∴，
解得，
∴当时，正方形与长方形的重叠部分为三角形，
∴时，正方形与长方形的重叠部分为三角形；
如图4，当Q点运动与C点时，，此时正方形与长方形的重叠部分为三角形；
∴时，正方形与长方形的重叠部分为四边形，
如图5，

＝
＝；
综上所述：当时，；当时， ；
（4）由（3）可知当时，正方形与长方形的重叠部分为三角形；
当时，正方形与长方形的重叠部分为三角形；
综上所述：当或时，正方形与长方形的重叠部分为三角形．
【变式训练3】已知在矩形ABCD中，AB＝4，AD＝9，点M在AD上，且AM＝4，动点P从点B出发，以每秒1个单位长度的速度，沿B﹣C﹣D﹣A向终点A运动，运动时间为t秒．
(1)当点P在BC边上时，BP＝ ，CP＝ ．（用含t的代数式表示）
(2)点P在运动过程中，△ABP是直角三角形时，t的取值范围为 ．
(3)点P在运动过程中，△DMP是等腰三角形时，t的值为 ．
(4)连接CM，当点P在线段CM的垂直平分线上时，t的值为 ．
【答案】(1)t，9﹣t
(2)0＜t≤9或13≤t＜22
(3)1或7或6.5
(4)4.9或13.9
【解析】（1）
解：当点P在BC边上时，BP＝t，CP＝9﹣t，
故答案为：t，9﹣t；
（2）
当点P在线段BC，线段AD上运动时，△ABP是直角三角形．
因为BC=9，BC+CD=13，BC+CD+DA=22
∴t的取值范围：0＜t≤9或13≤t＜22．
故答案为：0＜t≤9或13≤t＜22；
（3）
过点M作MH⊥BC于点H，则四边形AMHB是矩形．
∴MH＝AB＝4，AM＝BH＝4，CH=DM＝AD﹣AM＝5．
∴PH=
∴当MP＝MD时，
，
∴t＝1或7．
当PM＝PD时，点P是CH的中点，BP＝BH+CH=4+2.5＝6.5，
∴t＝6.5，
综上所述，满足条件的t的值为1或7或6.5．
故答案为：1或7或6.5；
（4）
当点P在CM的垂直平分线上时，PM＝CP．
当点P在线段BC上时，CP=MP=9-t，PH=t-4，MH=4，
∵△MPH是直角三角形，
∴
即，
∴t＝4.9，
当点P在线段AD上时，同法可得PM＝CP
CP=MP=18-t，DP=t-13，CD=4
∵△CDP是直角三角形，
∴
即，
∴t＝13.9．
综上所述，满足条件的t的值为4.9或13.9．
故答案为：4.9或13.9．