初中数学总复习第四章几何初步知识与三角形第13课时几何初步知识及相交线平行线课件

这是一份初中数学总复习第四章几何初步知识与三角形第13课时几何初步知识及相交线平行线课件，共29页。PPT课件主要包含了内容索引，考点梳理，自主测试，答案B，答案C，答案D，答案70°，答案80°等内容，欢迎下载使用。

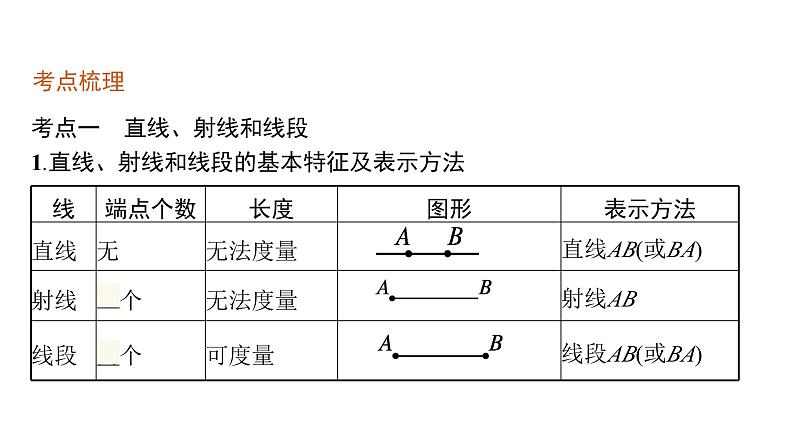
考点一　直线、射线和线段1.直线、射线和线段的基本特征及表示方法
2.直线的数学基本事实:经过两点有且只有一条直线,简称:两点确定一条直线.3.线段的数学基本事实:两点之间,线段最短.4.两点间的距离:连接两点之间线段的长度叫做两点间的距离.5.线段的中点:把一条线段分成两条相等的线段的点.
考点二　角1.(1)静态定义:有公共端点的两条射线组成的图形.(2)动态定义:角可以看作是一条射线绕着端点从起始位置(角的始边)旋转到终止位置(角的终边)所形成的图形.2.度量:角的度量单位为度、分、秒,即1°=60',1'=60″;1周角=2平角=4直角=360°.3.角的平分线:从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
4.(1)互余:如果两个角的和为90°,那么这两个角互为余角,简称互余,其中一个角是另一个角的余角.(2)互补:如果两个角的和为180°,那么这两个角互为补角,简称互补,其中一个角是另一个角的补角.(3)互余与互补的角的性质:同角或等角的余角相等;同角或等角的补角相等.
考点三　相交线1.对顶角:(1)定义:两条直线相交组成的四个角中,有公共顶点且没有公共边的两个角叫做对顶角.(2)性质:对顶角相等.2.邻补角:(1)定义:两条直线相交组成的四个角中,有公共边的两个角叫邻补角.(2)性质:邻补角互补.
3.三线八角:在同一平面内,两条直线被第三条直线相截所得的八个角称为“三线八角”.这八个角依照其相应位置的不同分别有不同的名称(如右图).(1)同位角:若两个角分别在两条直线相同的一侧,且都在截线的同旁,则称此两角为同位角(如图中的∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8).同位角的形状像字母F.
(2)内错角:若两个角位置交错,且都在两条直线之间,则称此两角为内错角(如图中的∠2和∠8,∠3和∠5).内错角的形状像字母Z.(3)同旁内角:若两个角都在两条直线之间,且在截线的同旁,则称此两角为同旁内角(如图中的∠2和∠5,∠3和∠8).同旁内角的形状像字母U或门框形.
考点四　垂线1.垂直的定义:两直线相交组成的四个角中,有一个角是直角,则这两条直线互相垂直,其中一条直线是另一条直线的垂线.2.垂线段的定义:如图,P为直线l外一点,PO⊥l,垂足为O,线段PO叫做垂线段,A,B为直线l上的两点,线段PA,PB叫做斜线段.
3.性质:(1)数学基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直;(2)定理:过直线外一点与直线上各点连接的所有线段中,垂线段最短.4.点到直线的距离:从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
考点五　平行线1.定义:在同一平面内,不相交的两条直线叫做平行线.用符号“∥”表示.2.两条直线的位置关系:在同一平面内,两条直线的位置关系有两种(不考虑重合):相交、平行.3.平行的数学基本事实:经过已知直线外一点,有且只有一条直线与已知直线平行.平行的传递性:如果两条直线都和第三条直线平行,那么这两条直线互相平行.
4.判断两条直线平行的方法:(1)平行线的定义;(2)平行的传递性;(3)同位角相等,两直线平行;(4)内错角相等,两直线平行;(5)同旁内角互补,两直线平行.5.平行线的性质:(1)两直线平行,同位角相等;(2)两直线平行,内错角相等;(3)两直线平行,同旁内角互补.
1. 如图,C,D是线段AB上两点.若CB=4 cm,DB=7 cm,且D是AC的中点,则AC的长为(　　)
A.3 cmB.6 cmC.11 cmD.14 cm
2.如图,已知直线AB,CD相交于点O,OE平分∠COB.若∠EOB=55°,则∠BOD的度数是(　　)A.35°B.55°C.70°D.110°
3.如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,∠ADE=35°,∠C=120°,则∠A为(　　)A.60°B.45°C.35°D.25°
4.如图,AB⊥AC,AD⊥BC,垂足分别为A,D.则图中能表示点到直线距离的线段共有(　　)A.2条B.3条C.4条D.5条
5.如图,a∥b,∠1=110°,∠3=40°,则∠2=　　　　　. 
6.如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°.在OB上有一点P,从点P射出一束光线经OA上的点Q反射后,反射光线QR恰好与OB平行,则∠QPB的度数是　　　　　. 
【例1】 在直线l上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E的距离.
解:(1)当点C在AB的延长线上时,如图.因为D是AB的中点,AB=16 cm,
所以DE=AE-AD=20-8=12(cm).
(2)当点C在BA的延长线上时,如图.由(1)知AD=8 cm,AE=20 cm.则DE=AE+AD=20+8=28(cm).综上可知,点D与点E的距离是12 cm或28 cm.
【例2】 如图,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30',则下列结论中不正确的是(　　)A.∠2=45°B.∠1=∠3C.∠AOD与∠1互为补角D.∠1的余角等于75°30'
【例3】 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°.若∠1=25°,∠2=70°,则∠B=　　　　　. 
解析:∵m∥n,∴∠2=∠BAC+∠1,∴∠BAC=∠2-∠1=45°,∴∠B=90°-∠BAC=45°.答案:45°