2024春七下数学第8章整式乘法和因式分解8.5综合与实践纳米材料的奇异特性上课课件（沪科版）

这是一份2024春七下数学第8章整式乘法和因式分解8.5综合与实践纳米材料的奇异特性上课课件（沪科版），共17页。
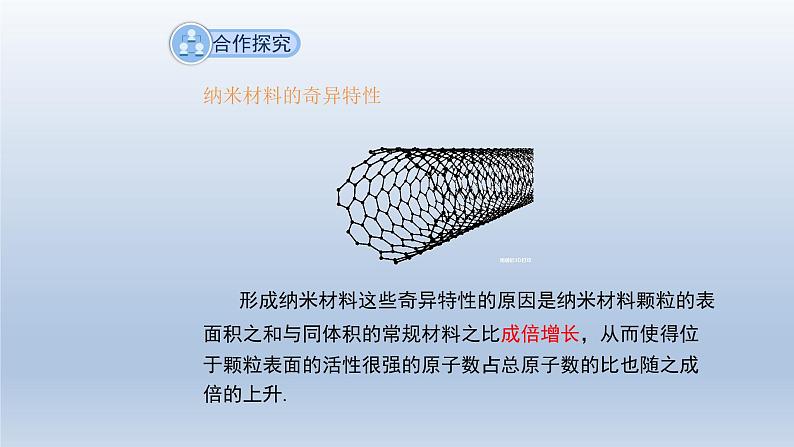
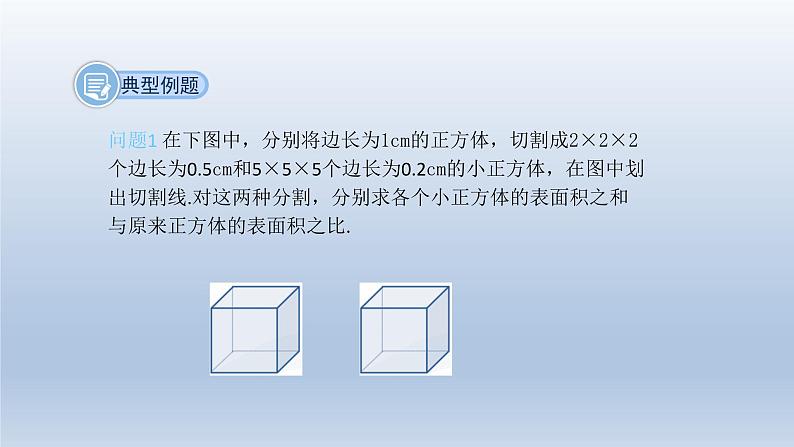
8.5 综合与实践纳米材料的奇异特性了解形成纳米材料特性的原因，分析探究将一个正方体进行n×n×n细分后表面积的变化情况.以问题为载体，学生自主参与探究学习活动，发展学生的创新意识与合作意识.经历数学活动的过程，增强自主探究问题的意识，养成学习数学，用数学的好习惯.了解纳米材料的实际用途，增强对数学的应用意识.什么是纳米(nm)？什么是纳米材料？纳米材料是指用结构尺寸在1~100nm的范围内的纳米颗粒制成的.纳米材料有许多奇异的特性.纳米材料的奇异特性常规银块熔点约900℃，而银纳米颗粒在100℃时即熔化.纳米材料的奇异特性 纳米颗粒结合成常规材料时的烧结温度也明显降低，一些高温陶瓷的制造，因烧结温度明显降低，大大降低了制造工艺难度和制造成本.纳米材料的奇异特性 由纳米颗粒烧结的陶瓷，还具有很好的韧性，纳米二氧化钛陶瓷在室温下可以弯曲，塑性形变高达100%，纳米陶瓷是不容易摔碎的.纳米材料的奇异特性 形成纳米材料这些奇异特性的原因是纳米材料颗粒的表面积之和与同体积的常规材料之比成倍增长，从而使得位于颗粒表面的活性很强的原子数占总原子数的比也随之成倍的上升.问题1 在下图中，分别将边长为1cm的正方体，切割成2×2×2个边长为0.5cm和5×5×5个边长为0.2cm的小正方体，在图中划出切割线.对这两种分割，分别求各个小正方体的表面积之和与原来正方体的表面积之比.棱长为1cm的正方体表面积为：6×1×1=6 cm²表面积之比为 2 : 1棱长为0.5cm的正方体总表面积为： 2×2×2×6×0.5×0.5=12 cm² 表面积增加，是原正方体表面积的2倍切割成2×2×2个边长为0.5cm的小正方体：棱长为1cm的正方体表面积为：6×1×1=6 cm²表面积之比为 5 : 1棱长为0.2cm的正方体总表面积为： 5×5×5×6×0.2×0.2=30 cm² 表面积增加，是原正方体表面积的5倍切割成5×5×5个边长为0.2cm的小正方体：问题2 将一个边长为1cm的正方体，切割成n×n×n个边长为 cm 的小长方体，求各个小正方体的表面积之和与原正方体的表面积之比.1n³6nn:1问题3 当n=107时，求各个小正方体的表面积之和与原正方体的表面积之比.1n³6nn:1当n=107时，表面积之比为107 :1 随着 n 值的增大，表面积之比变化趋势如何？ 随着 n 值的增大，小正方体的边长缩小，各小正方体的表面积之和与原来正方体的表面积之比增大.问题4 将问题2中的正方体边长改为a，结果如何？1n³6nn:1an³6nan:1表面积之比为 n : 1纳米材料奇异特性的原因是： 体积相同时，纳米材料颗粒的表面积之和与常规材料表面积之比成倍增长，从而使得位于颗粒表面的活性很强的原子数占总原子数的比也随之成倍的上升.1. 如图，将黑、白两种颜色的正六边形地砖拼成若干个图案，则第n个图案中白色地砖的块数应该为______. 分析：每个图案都比其前一个图案多4块白色地砖.第1个图案白色地砖数=6；第2个图案白色地砖数=6+4=6+4×1 ；第3个图案白色地砖数=6+4+4=6+4×2 ； …… 则第n个图形白色地砖的数量为：6+4(n-1)=4n+24n+22. 已知下列等式：①13 =12 ；②13 +23 =32 ；③13 +23 +33 =62 ；④13 +23 +33 +43 =102 … 根据规律分析：第⑤个等式是：第n个等式是：分析：1³+2³+3³+4³+5³=15³第n个等式为：因此，第⑤个等式为：规律探究