2024春九年级数学下学期期末学情评估试卷（安徽专版沪科版）

这是一份2024春九年级数学下学期期末学情评估试卷（安徽专版沪科版），共13页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

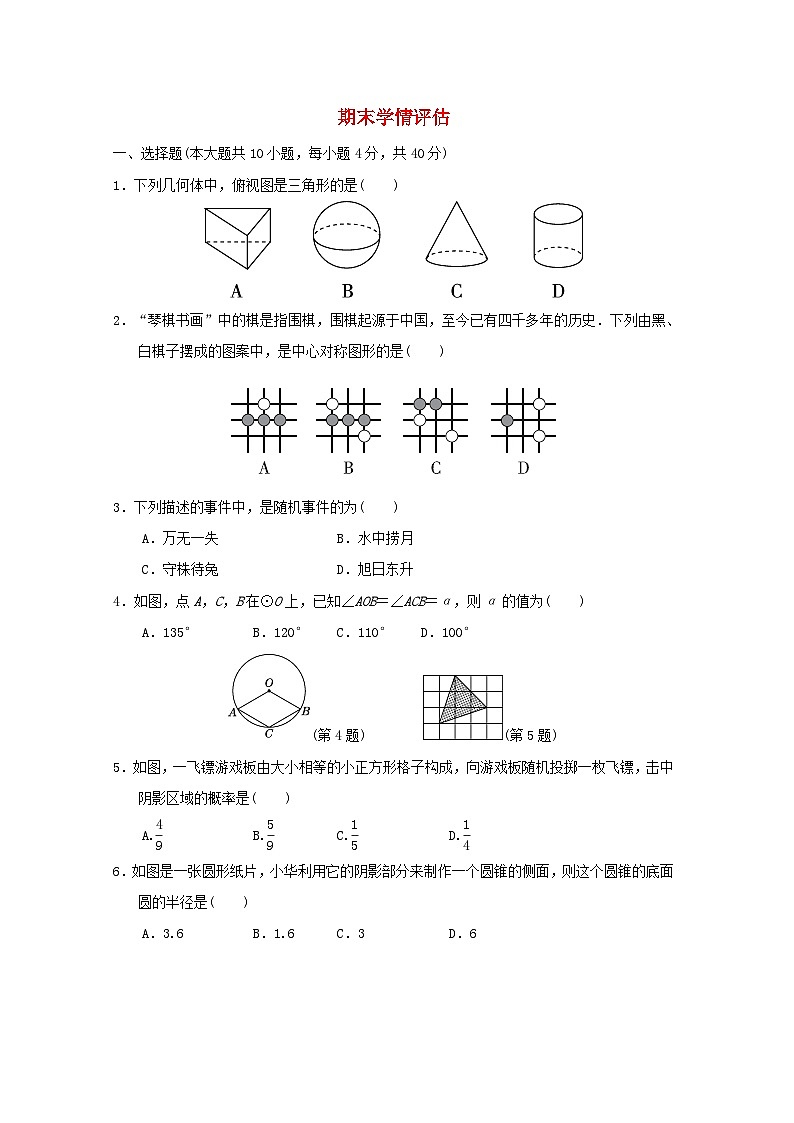
1．下列几何体中，俯视图是三角形的是( )
2．“琴棋书画”中的棋是指围棋，围棋起源于中国，至今已有四千多年的历史．下列由黑、白棋子摆成的图案中，是中心对称图形的是( )
3．下列描述的事件中，是随机事件的为( )
A．万无一失 B．水中捞月
C．守株待兔 D．旭日东升
4．如图，点A，C，B在⊙O上，已知∠AOB＝∠ACB＝α，则α的值为( )
A．135° B．120° C．110° D．100°
(第4题) (第5题)
5．如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中阴影区域的概率是( )
A.eq \f(4,9) B.eq \f(5,9) C.eq \f(1,5) D.eq \f(1,4)
6．如图是一张圆形纸片，小华利用它的阴影部分来制作一个圆锥的侧面，则这个圆锥的底面圆的半径是( )
A．3.6 B．1.6 C．3 D．6
(第6题) (第7题)
7.某三棱柱的三视图如图所示，已知俯视图中tan B＝eq \f(1,2)，BC＝7，下列结论不正确的是( )
A．m＝3 B．n＝2
C．tan C＝eq \f(3,2) D．S△ABC＝7
8．如图，点O是△ABC的内心，也是△DBC的外心．若∠A＝80°，则∠D的度数是( )
A．60° B．65° C．70° D．75°
(第8题) (第9题)
9.如图，在△ABC中，CA＝CB，∠ACB＝90°，以AB的中点D为圆心，作圆心角为90°的扇形EDF，点C恰好在eq \(EF,\s\up8(︵))上，设∠BDF＝α(0°＜α＜90°)．当α由小到大变化时，图中阴影部分的面积( )
A．由小变大B．由大变小
C．不变D．先由小变大，后由大变小
10．如图，CD是△ABC的高，若AB＝2，∠ACB＝45°，则CD的最大值为( )
A．1＋eq \r(2) B．4－eq \r(2)
C．2 D．4
(第10题) (第11题) (第12题)
二、填空题(本大题共4小题，每小题5分，共20分)
11．如图，在离某围墙AB 6米处有一棵树CD，在某时刻2米长的竹竿垂直地面，太阳光下的影长为3米，此时，树的影子有一部分映在地面上，还有一部分映在墙上AE处，墙上的影子高为4米，那么这棵树的高度约为________米．
12．如图，在4×4的正方形网格图中，已知点A，B，C，D，O均在格点上，且A，B，D在⊙O上，点E是线段CD与⊙O的交点，则∠BAE的正切值为________．
13．“宫商角徵羽”是中国古乐的五个基本音阶，是采用“三分损益法”获得的．现有一款“一起听古乐”的音乐玩具，音乐小球从A处沿轨道进入小洞就可以发出相应的声音，且小球进入每个小洞的可能性大小相同．现有一个音乐小球从A处先后两次进入小洞，先发出“商”音，再发出“羽”音的概率是________．
(第13题) (第14题)
14．如图，在△ABC中，AD是BC边上的中线，以AB为直径的⊙O恰好交BC于点D，过点D作MN⊥AC于点M，交AB的延长线于点N，过点B作BG⊥MN于点G，AB＝6，∠DAC＝30°.
(1)eq \(BD,\s\up8(︵))的长为________；
(2)BG＋AM的值为________．
三、(本大题共2小题，每小题8分，共16分)
15．图①是由5个大小相同的小正方体搭成的几何体，其中每个小正方体的棱长为1 cm.

(第15题)
(1)直接写出这个几何体的表面积(包含底面面积)：________；
(2)请按要求在如图②所示的边长为1的正方形网格内画出这个几何体的三视图．
16．在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共40个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，然后把它放回口袋中，不断重复，共摸球1 000次，其中有600次摸到白球，试估算口袋中黑、白两种颜色的球各有多少个．
四、(本大题共2小题，每小题8分，共16分)
17．如图，在平面直角坐标系中，△ABC的顶点的坐标分别为A(2，3)，B(2，1)，C(5，1)，
(第17题)
把△ABC绕着点A按顺时针方向旋转90°得到△AEF，点B的对应点为E，点C的对应点为F.
(1)在图中画出△AEF；
(2)点C的运动路径长为____________；
(3)旋转过程中线段BC扫过的面积为____________．
18．如图，AB为⊙O的直径，点C，D在⊙O上，连接AC，BC，C是eq \(BD,\s\up8(︵))的中点，过点C作AD的垂线EF，交AD的延长线于点E.
(1)求证：EF是⊙O的切线；
(2)若AB＝5，BC＝3，求线段AE的长．
(第18题)
五、(本大题共2小题，每小题10分，共20分)
19．一个不透明的箱子里装有2个红色小球和若干个白色小球，每个小球除颜色外其他完全相同，每次把箱子里的小球摇匀后随机摸出1个小球，记下颜色后再放回箱子里，通过大量重复试验后，发现摸到白色小球的频率稳定在0.33左右．
(1)请你估计箱子里白色小球的个数；
(2)现从该箱子里摸出1个小球，记下颜色后放回箱子里，摇匀后，再摸出1个小球，求两次摸出的小球颜色恰好不同的概率．(用画树状图或列表的方法)
20．如图，四边形ABCD内接于⊙O，AB是直径，D是eq \(AC,\s\up8(︵))的中点，连接AC交OD于点E.
(1)求证：OD∥BC；
(2)若AC＝8，DE＝2，求⊙O的半径．
(第20题)
六、(本题满分12分)
21．如图，在平面直角坐标系xOy中，点P(2，3)是一个光源．木杆AB两端的坐标分别为A(0，1)，B(3，1)．木杆AB在x轴上的投影为CD.
(1)实际操作：利用尺规过点P作CD的垂线，垂足为M，交AB于点N(要求：尺规作图并保留作图痕迹，不写作法，标明字母)．
(2)解决问题：求CD的长．
(第21题)
七、(本题满分12分)
22．如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，5为半径作⊙O，与∠EPF的边PF交于A，B两点，连接OA，此时有OA∥PE.
(1)求证：AP＝AO；
(2)若弦AB＝8，求tan∠POA的值．
(第22题)
八、(本题满分14分)
23．如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD，CD，过点D作BC的平行线与AC的延长线相交于点P.
(1)求证：PD是⊙O的切线；
(2)求证：△ABD∽△DCP；
(3)若AB＝6，AC＝8，直接写出点O到AD的距离．
(第23题)
答案
一、1.A 2.B 3.C 4.B 5.C 6.A
7.C 思路点睛：在其俯视图中过点A作AD⊥BC于点D，根据这个几何体的三视图，可知BD＝4，CD＝m，AD＝n，根据锐角三角函数的定义、线段的长度关系、三角形的面积公式分别对各个结论进行判断即可.
8.B 点拨：连接OB，OC，如图，
（第8题）
∵点O是△ABC的内心，
∴∠OBC＝eq \f(1,2)∠ABC，∠OCB＝eq \f(1,2)∠ACB，
∴∠OBC＋∠OCB＝eq \f(1,2)∠ABC＋eq \f(1,2)∠ACB＝eq \f(1,2)（∠ABC＋∠ACB）＝eq \f(1,2)（180°－∠A）＝50°，
∴∠BOC＝180°－（∠OBC＋∠OCB）＝130°.
∵点O是△DBC的外心，∴∠D＝eq \f(1,2)∠BOC＝65°.
9.C
10.A 点拨：在AB上方作以AB为斜边的等腰直角三角形AOB.
∵∠ACB＝45°，
∴点C在以O为圆心，OA为半径的圆上运动.
∵AB＝2，∴OA＝OC＝eq \r(2)，
当CD经过圆心O时，CD最长.
∵CD是△ABC的高，
∴易知AD＝BD＝OD＝eq \f(1,2)AB＝1，
此时CD＝OC＋OD＝eq \r(2)＋1.
二、11.8 12.eq \f(1,2) 13.eq \f(1,25)
14.（1）π （2）6
三、15.解：（1）22 cm2
（2）如图所示.
（第15题）
16.解：设白球的个数为x，
则eq \f(x,40)＝eq \f(600,1 000)，解得x＝24，40－24＝16.
答：估计口袋中白球有24个，黑球有16个.
四、17.解：（1）如图所示，△AEF即为所作.
（第17题）
（2）eq \f(\r(13),2)π 点拨：易知AC＝eq \r(22＋32)＝eq \r(13)，
∠CAF＝90°，
∴点C的运动路径长为eq \f(90·π· \r(13),180)＝eq \f(\r(13),2)π.
（3）eq \f(9,4)π 点拨：旋转过程中线段BC扫过的面积为
eq \f(90·π·（ \r(13)）2,360)－eq \f(90·π·22,360) ＝eq \f(13,4)π－π＝eq \f(9,4)π.
18.（1）证明：如图，连接OC.
（第18题）
∵OA＝OC，∴∠OCA＝∠BAC.
∵C是eq \(BD,\s\up8(︵))的中点，∴eq \(CD,\s\up8(︵))＝eq \(BC,\s\up8(︵))，
∴∠EAC＝∠BAC，∴∠EAC＝∠OCA，
∴OC∥AE.∵AE⊥EF，∴OC⊥EF.
∵OC是⊙O的半径，∴EF是⊙O的切线.
（2）解：∵AB为⊙O的直径，∴∠BCA＝90°，
∴AC＝eq \r(AB2－BC2)＝4.∵EF⊥AD，
∴∠AEC＝90°＝∠ACB.又∵∠EAC＝∠CAB，
∴△AEC∽△ACB，∴eq \f(AE,AC)＝eq \f(AC,AB)，即eq \f(AE,4)＝eq \f(4,5)，
∴AE＝eq \f(16,5).
五、19.解：（1）因为通过大量重复试验后，发现摸到白色小球的频率稳定在0.33左右，0.33≈eq \f(1,3)，
所以估计摸到白色小球的概率为eq \f(1,3)，
设箱子里白色小球有x个，根据题意可得eq \f(x,x＋2)＝eq \f(1,3)，
解得x＝1，经检验，x＝1是该分式方程的根.
答：估计箱子里白色小球的个数为1.
（2）画树状图如图.
（第19题）
由图知，共有9种等可能的结果，其中两次摸出的小球颜色恰好不同的结果有4种.
所以两次摸出的小球颜色恰好不同的概率为eq \f(4,9).
20.（1）证明：如图，连接OC，
∵D是eq \(AC,\s\up8(︵))的中点，
∴∠AOD＝∠COD＝eq \f(1,2)∠AOC.
又∵∠B＝eq \f(1,2)∠AOC，
∴∠B＝∠AOD，∴OD∥BC.
（第20题）
（2）解：设⊙O的半径为r，则OD＝OC＝r，
∵DE＝2，∴OE＝r－2.∵OA＝OC，∠AOD＝∠COD，
∴OD⊥AC，∴∠CEO＝90°，EC＝eq \f(1,2)AC＝eq \f(1,2)×8＝4，
在Rt△CEO中，OC2＝CE2＋OE2，
即r2＝42＋（r－2）2，解得r＝5，
∴⊙O的半径为5.
六、21.解：（1）如图.
（第21题）
（2）∵A（0，1），∴OA＝1.
易知四边形OANM为矩形，
∴OA＝MN＝1.∵A（0，1），B（3，1），
∴AB∥x轴，AB＝3.∴△PAB∽△PCD.
∵点P（2，3），∴PM＝3，
∴PN＝PM－MN＝3－1＝2，
∴eq \f(AB,CD)＝eq \f(PN,PM)，∴eq \f(3,CD)＝eq \f(2,3)，∴CD＝eq \f(9,2)，即CD的长为eq \f(9,2).
七、22.（1）证明：∵OA∥PE，∴∠OPE＝∠POA.
∵PG平分∠EPF，∴∠OPE＝∠OPA，
∴∠OPA＝∠POA，∴AP＝AO.
（2）解：如图，过点O作OH⊥AB于点H，
（第22题）
∵AB＝8，∴AH＝eq \f(1,2)AB＝4，
∴OH＝eq \r(OA2－AH2)＝eq \r(52－42)＝3.
∵AP＝AO，∠OPA＝∠POA，
∴tan∠POA＝tan∠APO＝eq \f(OH,PH)＝eq \f(3,5＋4)＝eq \f(1,3).
八、23.（1）证明：如图，连接OD.
（第23题）
∵点O在BC边上，
∴BC是⊙O的直径.∴∠BAC＝90°.∵AD平分∠BAC，
∴∠BAD＝∠DAC＝eq \f(1,2)∠BAC＝45°，
∴∠BOD＝2∠BAD＝90°.
∵BC∥DP，∴∠ODP＝∠BOD＝90°.∴OD⊥DP.
又∵OD是⊙O的半径，∴PD是⊙O的切线.
（2）证明：∵BC∥DP，
∴∠ACB＝∠P.∵∠ACB＝∠ADB，∴∠ADB＝∠P.
∵四边形ABDC为⊙O的内接四边形，
∴易得∠ABD＝∠DCP.∴△ABD∽△DCP.
（3）解：点O到AD的距离为eq \f(\r(2),2).
点拨：过点O作OE⊥AD于点E.∵∠BAC＝90°，
∴BC＝eq \r(AB2＋AC2)＝10.∵BC是⊙O的直径，
∴∠BDC＝90°，易知BD＝DC，
∴BD2＋DC2＝2BD2＝BC2，∴BD＝DC＝5 eq \r(2).
由（2）知△ABD∽△DCP，∴eq \f(AB,DC)＝eq \f(BD,CP)，
∴CP＝eq \f(BD·DC,AB)＝eq \f(5 \r(2)×5 \r(2),6)＝eq \f(25,3)，
∴AP＝AC＋CP＝8＋eq \f(25,3)＝eq \f(49,3).
∵∠ADB＝∠P，∠BAD＝∠DAP，
∴△BAD∽△DAP，∴eq \f(AB,AD)＝eq \f(AD,AP)，
∴AD2＝AB·AP＝6×eq \f(49,3)＝98，∴AD＝7 eq \r(2)（负值舍去）.
∵OE⊥AD，∴ED＝eq \f(1,2)AD＝eq \f(7 \r(2),2).
在Rt△OED中，OE＝eq \r(OD2－ED2)＝eq \r(52－\b\lc\(\rc\)(\a\vs4\al\c1(\f(7 \r(2),2)))\s\up12(2))＝eq \f(\r(2),2)，
∴点O到AD的距离为eq \f(\r(2),2).