初中数学沪科版七年级下册8.3 完全平方公式与平方差公式课堂教学课件ppt

这是一份初中数学沪科版七年级下册8.3 完全平方公式与平方差公式课堂教学课件ppt，共22页。PPT课件主要包含了多项式与多项式相乘，a+bp+q，x21，m24，x212，m222，2x212，平方差公式，S2S3，S1+S3等内容，欢迎下载使用。
能根据多项式的乘法法则推导出平方差公式，理解平方差公式的结构特征，并能正确运用公式进行计算.在利用几何图形的面积验证公式的过程中，了解平方差公式的几何意义，感知数形结合的思想.在探索平方差公式的过程中，感悟从一般到特殊、从具体到抽象地研究问题的方法.在探究过程中发现规律，并能用符号表示，感受数学的严谨性，体会数学的简洁美.
先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.
=ap+aq+bp+bq
多项式与多项式相乘的法则
计算下列多项式的积，看谁算得又快又对？
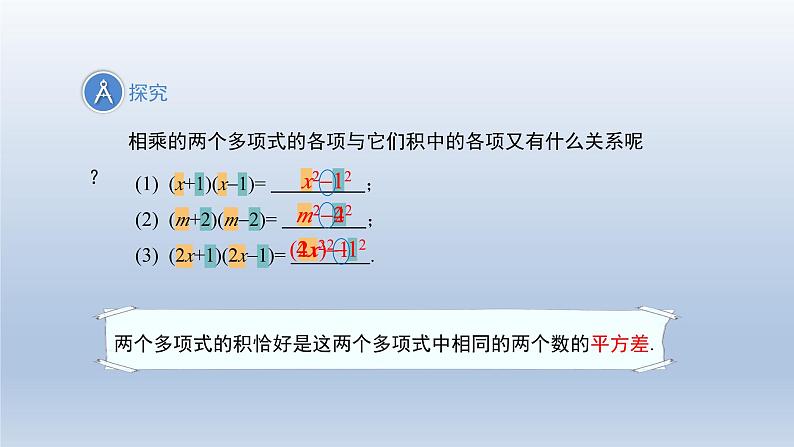
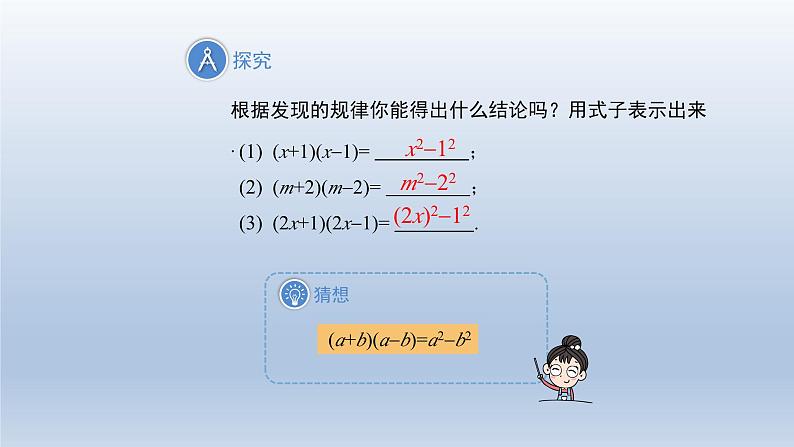
(x+1)(x1)= ； (m+2)(m2)= ； (2x+1)(2x1)= .
观察上面的等式，你能发现什么规律？
下列问题中相乘的两个多项式有什么共同点？
均为相同的两个数的和、两个数的差的形式.
相乘的两个多项式的各项与它们积中的各项又有什么关系呢？
两个多项式的积恰好是这两个多项式中相同的两个数的平方差.
根据发现的规律你能得出什么结论吗？用式子表示出来.
(a+b)(ab)=a2b2
你能对发现的规律进行推导吗？
(a+b)(ab)=a2ab+abb2=a2b2
两个数的和与这两个数的差的积，等于这两个数的平方差.
你能根据图中的图形面积说明平方差公式吗？
=(a+b)(ab)
(相同项)2(相反项)2
等号左边是两个二项式的积，且这两个二项式中有一项为相同项，另一项为相反项.
等号右边是相同项的平方减去相反项的平方.
公式中的字母可以表示具体的数，也可以表示单项式或多项式等式子.
判断下列式子是否能用平方差公式计算：
(1) (a+2b)(a−2b)(2) (a−2b)(2b−a) (3) (2ab)(b+2a)(4) (a−3b)(a+3b) (5) (2x+3y)(3y−2x)
a2−(3b)2 
符合平方差公式的特征才能运用平方差公式计算.
【例1】利用乘法公式计算：
(1) 1999×2001； (2) (x+3)(x3)(x2+9).
(1) 1999×2001=(20001)×(2000+1)=20002 12=3 999 999
(2) (x+3)(x3)(x2+9)=(x29)(x2+9)=x481.
【例2】计算：
(1) (a+b+c)2 ； (2) (ab)3.
(1) (a+b+c)2 =[(a+b)+c]2=(a+b)2+2(a+b)c+c2=a2+2ab+b2+2ac+2bc+c2=a2+b2+c2+2ab+2ac+2bc.
(2) (ab)3 =(ab) (ab)2 =(ab)(a22ab+b2)=a32a2b+ab2a2b+2ab2b3 =a33a2b+3ab2b3.
1. 利用乘法公式计算：
(1) (2a+5b)(2a5b)； (2) ( x3)( x+3)； (3) (y2x)(2xy)； (4) (xy+1)(xy1).
(1) (2a+5b)(2a5b)=(2a)2(5b)2=4a225b2
(2) ( x3)( x+3) =( x)29= x29
(3)(y2x)(2xy) =(2x)2y2=4x2y2
(4) (xy+1)(xy1)=(xy)21=x2y21
2. 利用乘法公式计算：
(1) 598×602； (2) 9992.
(1) 598×602 =(6002)× (600+2)=600222=359 996
(2) 9992 =(10001)2=100022000+12=998 001
(1) (a+b)3 ； (2) (x5)3.
(1) (a+b)3 =(a+b) (a+b)2 =(a+b)(a2+2ab+b2)=a3+2a2b+ab2+a2b+2ab2+b3 =a3+3a2b+3ab2+b3.
(2) (x5)3=(x5) (x5)2=(x5)(x210x+25)=x310x2+25x5x2+50x125 =x315x2+75x125.
4. 计算：(abc)2
(abc)2=[(ab)c]2=(ab)22(ab)c+c2=a22ab+b22ac+2bc+c2=a2+b2+c22ab2ac+2bc.