初中数学沪科版九年级下册24.3.2 圆内接四边形作业ppt课件

这是一份初中数学沪科版九年级下册24.3.2 圆内接四边形作业ppt课件，共34页。PPT课件主要包含了答案呈现，答案C，答案A，点方法，答案D等内容，欢迎下载使用。

下列说法中正确的是(　　)A．在圆内部的多边形叫做圆内接多边形B．过四边形四个顶点的圆叫做这个四边形的外接圆C．任意一个四边形都有外接圆D．一个圆只有唯一一个内接四边形
[2022·株洲]如图，等边三角形ABC的顶点A在⊙O上，边AB，AC与⊙O分别交于点D，E，点F是劣弧DE上一点，且与D，E不重合，连接DF，EF，则∠DFE的度数为(　　)A．115° B．118°C．120° D．125°
易知四边形EFDA是⊙O的内接四边形，∴∠DFE＋∠A＝180°.∵△ABC是等边三角形，∴∠A＝60°.∴∠DFE＝120°．
[2022·长春]如图，四边形ABCD是⊙O的内接四边形，若∠BCD＝121°，则∠BOD的度数为(　　)A．138° B．121° C．118° D．112°
∵四边形ABCD是⊙O的内接四边形，∴∠A＋∠BCD＝180°.∴∠A＝180°－121°＝59°.∴∠BOD＝2∠A＝2×59°＝118°.
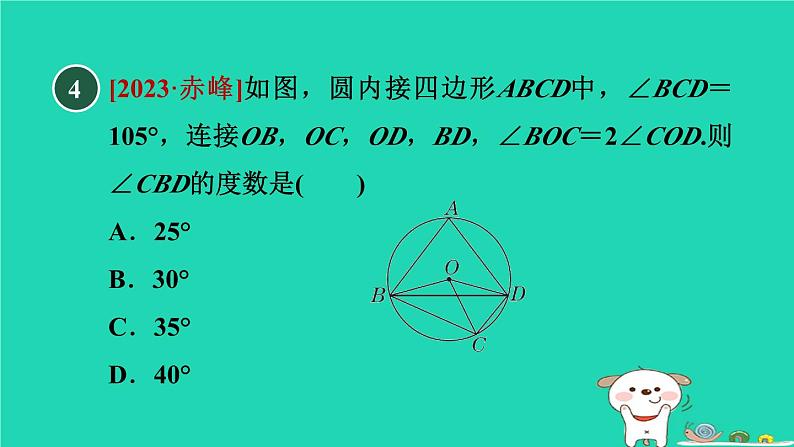
[2023·赤峰]如图，圆内接四边形ABCD中，∠BCD＝105°，连接OB，OC，OD，BD，∠BOC＝2∠COD.则∠CBD的度数是(　　)A．25° B．30° C．35° D．40°
利用圆内接四边形的性质及圆周角定理求得∠BOD的度数，再结合已知条件求得∠COD的度数，然后利用圆周角定理求得∠CBD的度数．
∵DB⊥AC，∴∠AFD＝90°.∴∠CAD＝∠BDA＝45°.∴∠AOB＝2∠ADB＝90°，∠COD＝2∠CAD＝90°.∵∠AOD＝120°，∴∠BOC＝360°－90°－90°－120°＝60°.∵OB＝OC，∴△OBC是等边三角形．∴BC＝OB.
[2023·宁夏]如图，四边形ABCD内接于⊙O，延长AD至点E，已知∠AOC＝140°，那么∠CDE＝________°.
如图，四边形ABCD是⊙O的内接四边形，AD与BC的延长线交于点E，BA与CD的延长线交于点F，∠DCE＝80°，∠F＝25°，则∠E的度数为(　　)A．55° B．50°C．45° D．40°
由三角形的外角性质得∠B＝∠DCE－∠F＝55°，∵四边形ABCD是⊙O的内接四边形，∴∠EDC＝∠B＝55°.∴∠E＝180°－∠DCE－∠EDC＝45°.
如图，四边形ABCD内接于⊙O，P为边AD上任意一点(点P不与点A，D重合)，连接CP，若∠B＝120°，则∠APC可能为(　　)A．30° B．45°C．50° D．65°
∵四边形ABCD内接于⊙O，∴∠B＋∠D＝180°.∵∠B＝120°，∴∠D＝180°－∠B＝60°.∵∠APC为△PCD的外角，∴∠APC＞∠D，只有D满足题意．故选D.
圆内接四边形的一组对角其实是圆中一条弦所对的两个圆周角，因此，在同圆或等圆中，相等的弦所对的圆周角相等或互补．
如图，四边形ABCD内接于⊙O，BC为⊙O的直径，OA∥CD.
(1)若∠ABC＝70°，求∠BAD的度数；
【解】∵OA＝OB，∠ABC＝70°，∴∠ABO＝∠BAO＝70°，∴∠BOA＝40°.∵OA∥CD，∴∠C＝∠BOA＝40°.∵四边形ABCD是⊙O的内接四边形，∴∠C＋∠BAD＝180°.∴∠BAD＝140°.
[2023·北京]如图，圆内接四边形ABCD的对角线AC，BD交于点E，BD平分∠ABC，∠BAC＝∠ADB.
(1)试说明：DB平分∠ADC，并求∠BAD的大小；
【解】∵∠BAC＝∠ADB，∠BAC＝∠CDB，∴∠ADB＝∠CDB.∴DB平分∠ADC.∵BD平分∠ABC，∴∠ABD＝∠CBD.∵四边形ABCD是圆内接四边形，∴∠ABC＋∠ADC＝ 180°.
∴∠ABD＋∠CBD＋∠ADB＋∠CDB＝180°.∴2(∠ABD＋∠ADB)＝180°.∴∠ABD＋∠ADB＝90°.∴∠BAD＝180°－90°＝90°.
(2)过点C作CF∥AD交AB的延长线于点F，若AC＝AD，BF＝2，求此圆半径的长．
【解】∵∠BAD＝90°，∴∠BAE＋∠DAE＝90°.又∵∠BAE＝∠ADE，∴∠ADE＋∠DAE＝ 90°.∴∠AED＝90°.∴BD⊥AC.∵∠BAD＝90°，∴BD是圆的直径．∴AE＝CE.∴AD＝CD.
∵∠ADC＋∠ABC＝180°，∠FBC＋∠ABC＝180°，∴∠FBC＝∠ADC＝ 60°.∴∠BCF＝30°.∴BC＝2BF＝4.∵BD是圆的直径，∴∠BCD＝90°.∵∠BDC＝30°，∴BD＝2BC＝8.∵BD是圆的直径，∴圆的半径长是4.
(1)求证：∠ADC－∠BAC＝90°(请用两种证法解答)；
【证明】证法一：如图，连接BD.∵AB是⊙O的直径，∴∠ADB＝90°.∵∠ADC－∠BDC＝∠ADB，∠BDC＝∠BAC，∴∠ADC－∠BAC＝90°.
证法二：如图，连接BC.∵AB是⊙O的直径，∴∠ACB＝90°.∵∠PBC＝∠BAC＋∠ACB，∴∠PBC－∠BAC＝ 90°.∵四边形ABCD为⊙O的内接四边形，∴∠ADC＋∠ABC＝180°.∵∠PBC＋∠ABC＝180°，∴∠ADC＝∠PBC.∴∠ADC－∠BAC＝90°.
(2)若∠ACP＝∠ADC，⊙O的半径为3，CP＝4，求AP的长．