





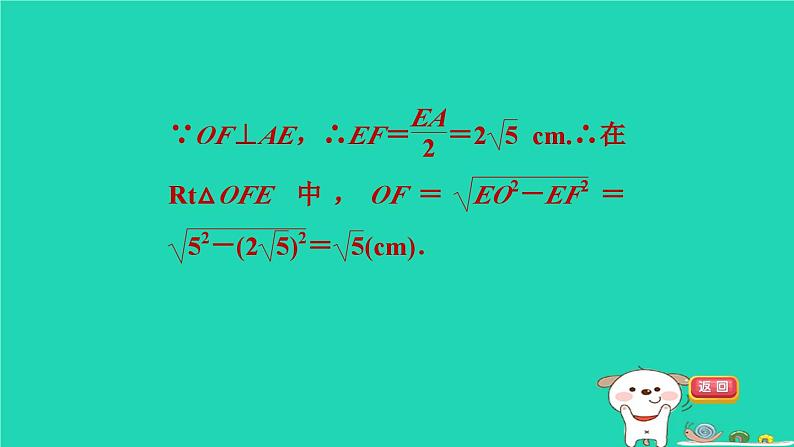
还剩27页未读,
继续阅读
2024春九年级数学下册第24章圆练素养构造圆的基本性质的基本图形的八大技法作业课件新版沪科版
展开
这是一份2024春九年级数学下册第24章圆练素养构造圆的基本性质的基本图形的八大技法作业课件新版沪科版,共35页。
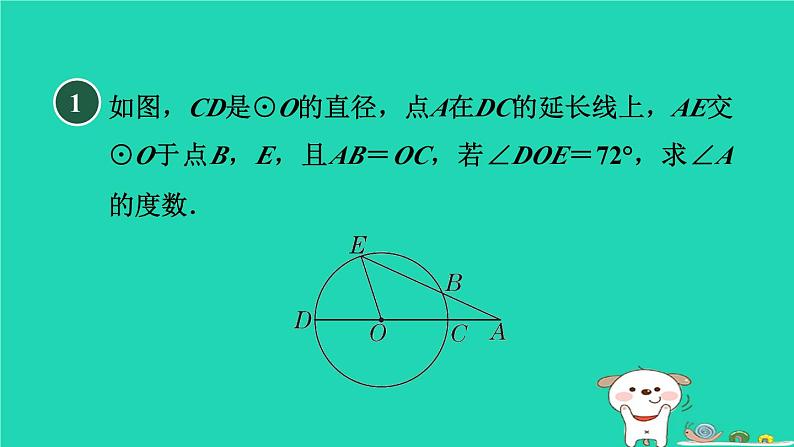
构造圆的基本性质的基本图形的八大技法练素养第24章 圆62°答 案 呈 现1如图,CD是⊙O的直径,点A在DC的延长线上,AE交⊙O于点B,E,且AB=OC,若∠DOE=72°,求∠A的度数.【解】如图,连接OB,∵点B,E在⊙O上,CD为⊙O的直径,∴OB=OE=OC.∴∠E=∠EBO.又∵AB=OC,∴OB=AB.∴∠A=∠AOB.又∵∠EBO=∠A+∠AOB,∴∠EBO=∠E=2∠A.又∵∠DOE=∠A+∠E,∴∠DOE=∠A+2∠A=72°.∴∠A=24°.2如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE上.已知AB=8 cm,CD=2 cm.(1)求⊙O的面积;【解】如图,连接OA.∵AB的中点C在直径DE上,AB=8 cm,∴OD⊥AB,AC=4 cm.设⊙O的半径为r cm,则OC=(r-2) cm.在Rt△OCA中,由勾股定理得(r-2)2+42=r2,解得r=5.∴⊙O的面积为π×52=25 π(cm2).(2)连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.3(1)求证:∠A=∠C;(2)若OD=DC,求∠A的度数.【解】设∠A=∠C=x°,∴∠POB=2∠A=2x°.∵OD=DC,∴∠DOC=∠C=x°.∵OP=OC,∴∠OPC=∠C=x°.在△POC中,x+x+2x+x=180,∴x=36.∴∠A=36°.4[2023·成都七中模拟]如图,A,B,C是⊙O的三等分点.(1)求∠AOB的度数;(2)若BO=4,求AB的长及△ABC的面积.5[2022·苏州]如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D=________.62° 【点拨】连接BC,构造直径AB所对的圆周角,进而求出∠B的度数,最后利用同弧所对的圆周角相等解决问题.如图,△ABC内接于⊙O,AD⊥BC于点D,连接AO.6(1)求证:∠BAD=∠CAO;【证明】如图,延长AO交⊙O于点E,连接CE,∴∠ACE=90°=∠ADB.又∵∠B=∠E,∴∠BAD=∠CAO.(2)若∠B=60°,AC=6,求OA的长.7(1)四边形EBFD是矩形;【证明】如图,连接BD.∵四边形ABCD是正方形,∴∠BAD=∠BCD=90°.∴BD为⊙O的直径.∴∠BED=∠BFD=90°.∵DF∥BE,∴∠EBF=180°-∠DFB=90°.∴∠BED=∠EBF=∠BFD=90°.∴四边形EBFD是矩形.(2)DG=BE.【点方法】常见的作辅助线的方法:1.有直径,通常作直径所对的圆周角,从而得出两直线互相垂直,简记为“见直径作直角”.2.有90°的圆周角,通常作直径,简记为“有直角作直径”.8(1)求⊙O半径的长;【解】如图,连接OA,OC,作OH⊥AC于点H.∵∠ABC=120°,∴∠AMC=180°-∠ABC=60°.∴∠AOC=2∠AMC=120°.(2)求证:AB+BC=BM.又∵BE=BC,∴△EBC是等边三角形.∴CE=CB=BE,∠CEB=60°.∴∠MEC=180°-∠CEB=120°=∠ABC.又∵∠CMB=∠CAB,∴△ABC≌△MEC(AAS).∴AB=ME.∵ME+EB=BM,∴AB+BC=BM.9(1)求证:AE=BE.(2)判断BE与EF是否相等,并说明理由.【解】BE=EF.理由如下:由(1)知∠BAC=90°,∴∠BAE+∠FAD=∠ABF+∠AFB=90°.又∵∠BAE=∠ABF,∴∠FAD=∠AFB.∴EF=AE.又∵AE=BE,∴BE=EF.(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB之间正确的关系式.【解】小李的发现是正确的.理由如下:如图,连接OA,CP,延长BA与CP,两线交于点G.
构造圆的基本性质的基本图形的八大技法练素养第24章 圆62°答 案 呈 现1如图,CD是⊙O的直径,点A在DC的延长线上,AE交⊙O于点B,E,且AB=OC,若∠DOE=72°,求∠A的度数.【解】如图,连接OB,∵点B,E在⊙O上,CD为⊙O的直径,∴OB=OE=OC.∴∠E=∠EBO.又∵AB=OC,∴OB=AB.∴∠A=∠AOB.又∵∠EBO=∠A+∠AOB,∴∠EBO=∠E=2∠A.又∵∠DOE=∠A+∠E,∴∠DOE=∠A+2∠A=72°.∴∠A=24°.2如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE上.已知AB=8 cm,CD=2 cm.(1)求⊙O的面积;【解】如图,连接OA.∵AB的中点C在直径DE上,AB=8 cm,∴OD⊥AB,AC=4 cm.设⊙O的半径为r cm,则OC=(r-2) cm.在Rt△OCA中,由勾股定理得(r-2)2+42=r2,解得r=5.∴⊙O的面积为π×52=25 π(cm2).(2)连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.3(1)求证:∠A=∠C;(2)若OD=DC,求∠A的度数.【解】设∠A=∠C=x°,∴∠POB=2∠A=2x°.∵OD=DC,∴∠DOC=∠C=x°.∵OP=OC,∴∠OPC=∠C=x°.在△POC中,x+x+2x+x=180,∴x=36.∴∠A=36°.4[2023·成都七中模拟]如图,A,B,C是⊙O的三等分点.(1)求∠AOB的度数;(2)若BO=4,求AB的长及△ABC的面积.5[2022·苏州]如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D=________.62° 【点拨】连接BC,构造直径AB所对的圆周角,进而求出∠B的度数,最后利用同弧所对的圆周角相等解决问题.如图,△ABC内接于⊙O,AD⊥BC于点D,连接AO.6(1)求证:∠BAD=∠CAO;【证明】如图,延长AO交⊙O于点E,连接CE,∴∠ACE=90°=∠ADB.又∵∠B=∠E,∴∠BAD=∠CAO.(2)若∠B=60°,AC=6,求OA的长.7(1)四边形EBFD是矩形;【证明】如图,连接BD.∵四边形ABCD是正方形,∴∠BAD=∠BCD=90°.∴BD为⊙O的直径.∴∠BED=∠BFD=90°.∵DF∥BE,∴∠EBF=180°-∠DFB=90°.∴∠BED=∠EBF=∠BFD=90°.∴四边形EBFD是矩形.(2)DG=BE.【点方法】常见的作辅助线的方法:1.有直径,通常作直径所对的圆周角,从而得出两直线互相垂直,简记为“见直径作直角”.2.有90°的圆周角,通常作直径,简记为“有直角作直径”.8(1)求⊙O半径的长;【解】如图,连接OA,OC,作OH⊥AC于点H.∵∠ABC=120°,∴∠AMC=180°-∠ABC=60°.∴∠AOC=2∠AMC=120°.(2)求证:AB+BC=BM.又∵BE=BC,∴△EBC是等边三角形.∴CE=CB=BE,∠CEB=60°.∴∠MEC=180°-∠CEB=120°=∠ABC.又∵∠CMB=∠CAB,∴△ABC≌△MEC(AAS).∴AB=ME.∵ME+EB=BM,∴AB+BC=BM.9(1)求证:AE=BE.(2)判断BE与EF是否相等,并说明理由.【解】BE=EF.理由如下:由(1)知∠BAC=90°,∴∠BAE+∠FAD=∠ABF+∠AFB=90°.又∵∠BAE=∠ABF,∴∠FAD=∠AFB.∴EF=AE.又∵AE=BE,∴BE=EF.(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB之间正确的关系式.【解】小李的发现是正确的.理由如下:如图,连接OA,CP,延长BA与CP,两线交于点G.
相关资料
更多









