2024春九年级数学下册第24章圆练素养旋转在解几何题中的十种常见技巧作业课件新版沪科版

这是一份2024春九年级数学下册第24章圆练素养旋转在解几何题中的十种常见技巧作业课件新版沪科版，共44页。

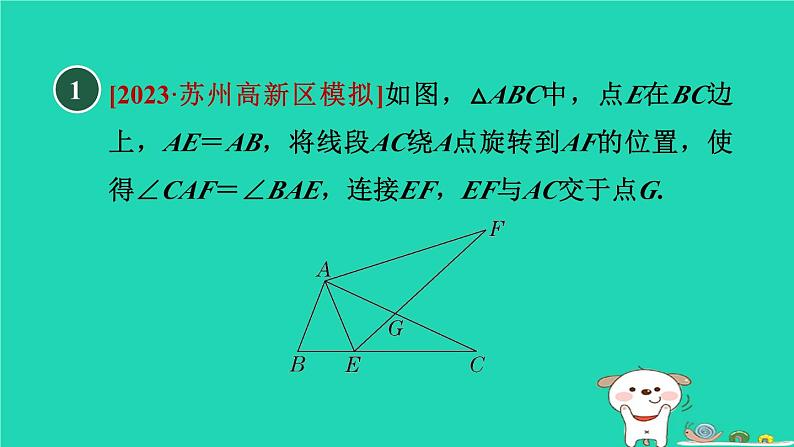
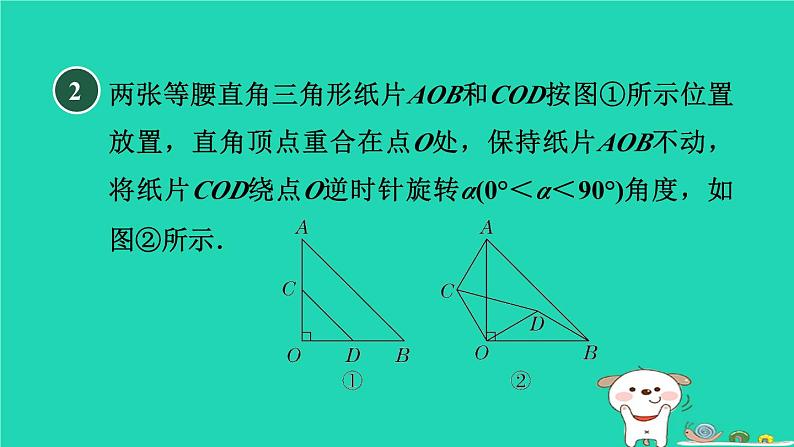
旋转在解几何题中的十种常见技巧练素养第24章 圆答 案 呈 现1[2023·苏州高新区模拟]如图，△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G.(1)求证：EF＝BC；【证明】∵∠BAE＝∠CAF，∴∠BAC＝∠EAF.∵将线段AC绕A点旋转到AF的位置，∴AC＝AF.又∵AB＝AE，∴△BAC≌△EAF(SAS)．∴EF＝BC.(2)若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．【解】∵AB＝AE，∠ABC＝65°，∴∠BAE＝180°－65°×2＝50°.∴∠FAG＝∠BAE＝50°.∵△BAC≌△EAF，∠ACB＝28°，∴∠F＝∠ACB＝28°.∴∠FGC＝∠FAG＋∠F＝50°＋28°＝78°.2两张等腰直角三角形纸片AOB和COD按图①所示位置放置，直角顶点重合在点O处，保持纸片AOB不动，将纸片COD绕点O逆时针旋转α(0°＜α＜90°)角度，如图②所示．(1)利用图②，求证：AC⊥BD；【证明】如图，延长BD交OA于点G，交AC于点E.由题意知，∠AOB＝∠COD＝90°，OA＝OB，OC＝OD，∴∠AOC＝∠BOD.∴△AOC≌△BOD(SAS)，∴∠CAO＝∠DBO.∵∠AOB＝90°，∠OGB＝∠AGE，∴∠AEG＝∠AOB＝90°，∴AC⊥BD.(2)如图③，当BD与CD在同一直线上时，AB＝25，AC＝7，求CD的长．3如图，在△ABC中，M是BC的中点，E，F分别在AC，AB上，且ME⊥MF，求证：EF