初中数学人教版九年级下册26.1.1 反比例函数随堂练习题

这是一份初中数学人教版九年级下册26.1.1 反比例函数随堂练习题，文件包含2613专题反比例函数中k的几何意义4大题型原卷版docx、2613专题反比例函数中k的几何意义4大题型解析版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。


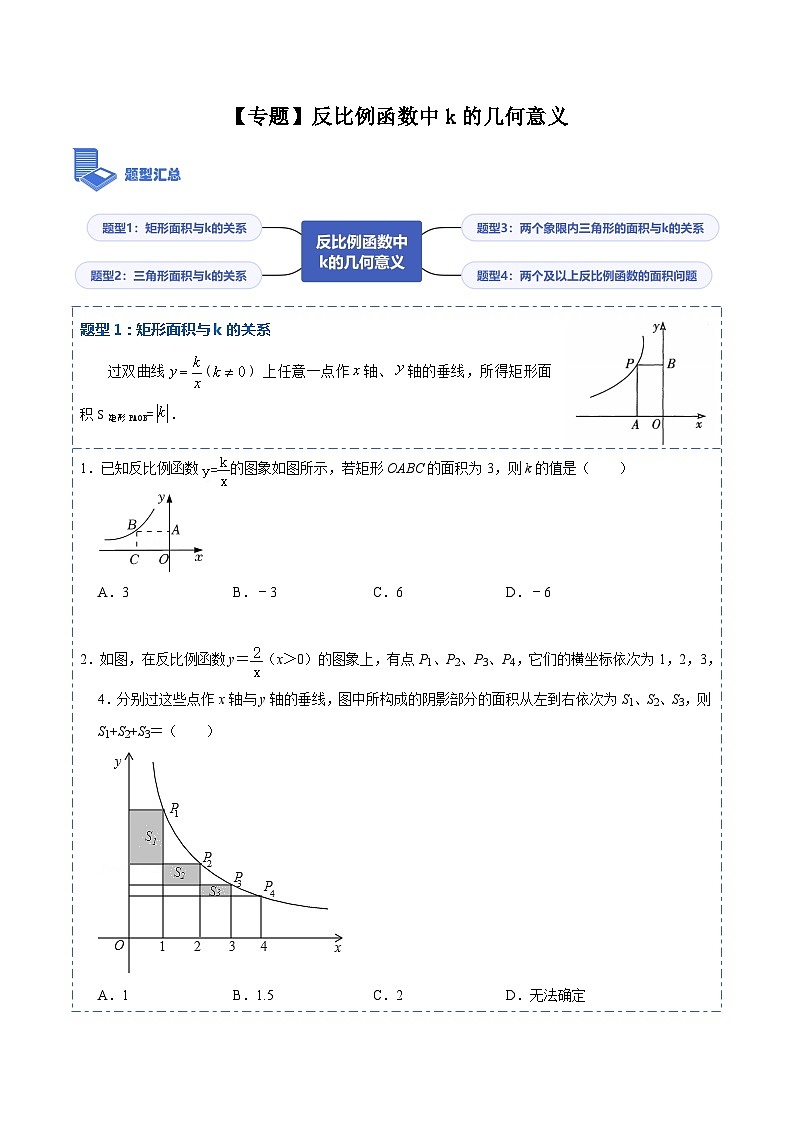
题型1：矩形面积与k的关系
过双曲线() 上任意一点作轴、轴的垂线，所得矩形面积S矩形PA0B=.
1．已知反比例函数的图象如图所示，若矩形OABC的面积为3，则k的值是（ ）
A．3B．﹣3C．6D．﹣6
【分析】根据反比例函数k的几何意义即可求出k的值．
【解答】解：∵矩形OABC的面积为3，
∴|k|＝3，
根据图象可知，k＜0，
∴k＝﹣3，
故选：B．
【点评】本题考查了反比例函数系数k的几何意义，熟练掌握这一性质是解题的关键．
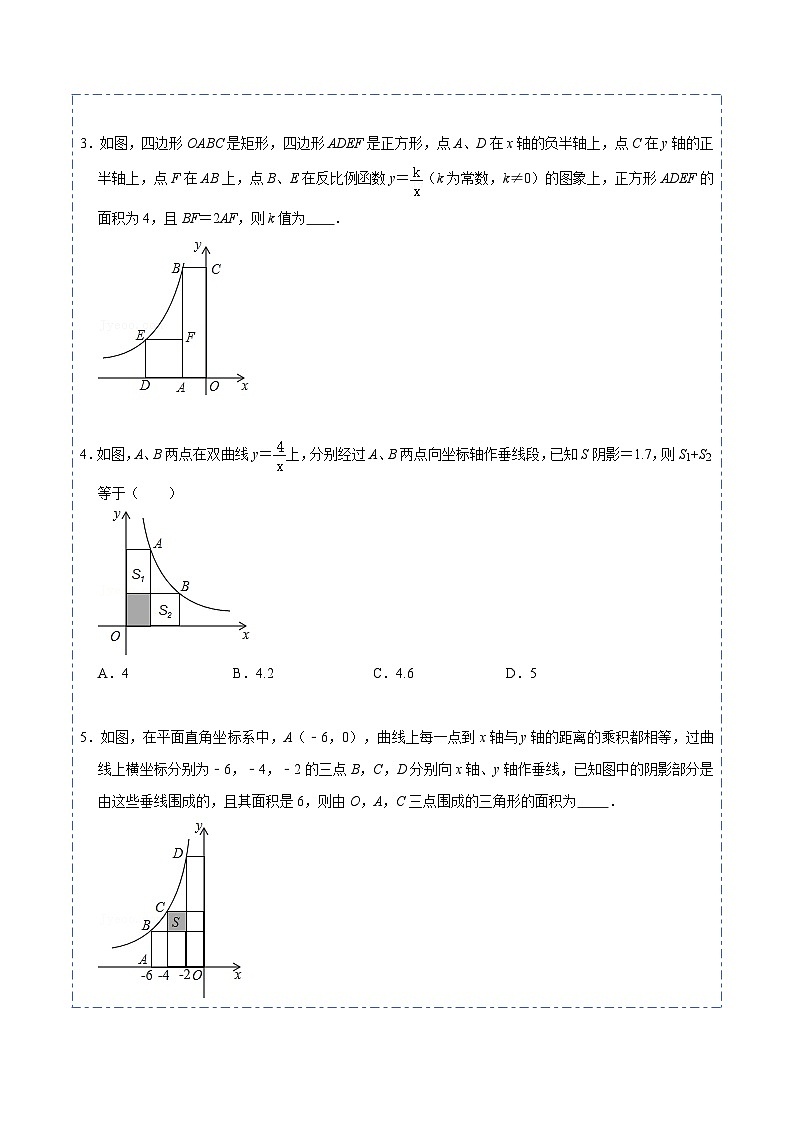
2．如图，在反比例函数y＝（x＞0）的图象上，有点P1、P2、P3、P4，它们的横坐标依次为1，2，3，4．分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1、S2、S3，则S1+S2+S3＝（ ）
A．1B．1.5C．2D．无法确定
【分析】根据反比例函数的几何意义可知图中所构成的阴影部分的面积和正好是从点P1向x轴，y轴引垂线构成的长方形面积减去最下方的长方形的面积．
【解答】解：由题意可知点P1、P2、P3、P4坐标分别为：（1，2），（2，1），（3，），（4，）．
∴由反比例函数的几何意义可知：S1+S2+S3＝2﹣1×＝＝1.5．
故选：B．
【点评】主要考查了反比例函数中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
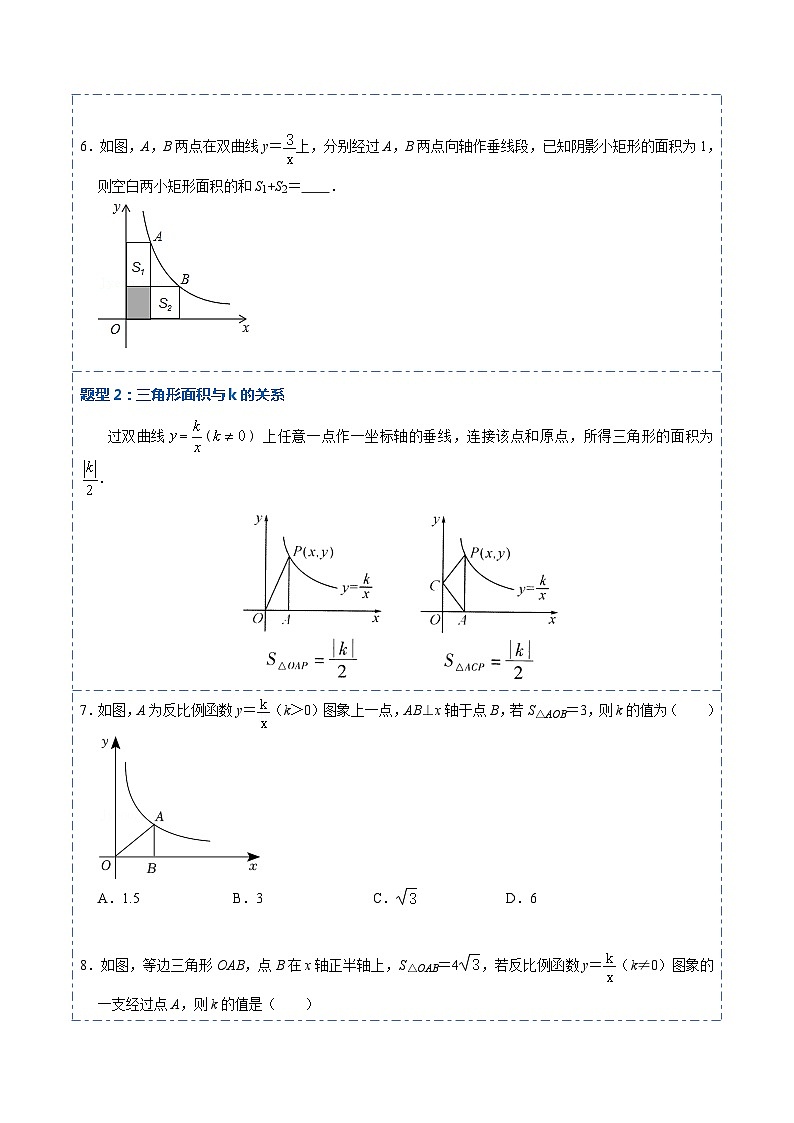
3．如图，四边形OABC是矩形，四边形ADEF是正方形，点A、D在x轴的负半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数y＝（k为常数，k≠0）的图象上，正方形ADEF的面积为4，且BF＝2AF，则k值为 ﹣6 ．
【分析】先由正方形ADEF的面积为4，得出边长为2，BF＝2AF＝4，AB＝AF+BF＝2+4＝6．再设B点坐标为（t，6），则E点坐标（t﹣2，2），根据点B、E在反比例函数y＝的图象上，利用根据反比例函数图象上点的坐标特征得k＝6t＝2（t﹣2），即可求出k＝﹣6．
【解答】解：∵正方形ADEF的面积为4，
∴正方形ADEF的边长为2，
∴BF＝2AF＝4，AB＝AF+BF＝2+4＝6．
设B点坐标为（t，6），则E点坐标（t﹣2，2），
∵点B、E在反比例函数y＝的图象上，
∴k＝6t＝2（t﹣2），
解得t＝﹣1，k＝﹣6．
故答案为﹣6．
【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数y＝（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy＝k．
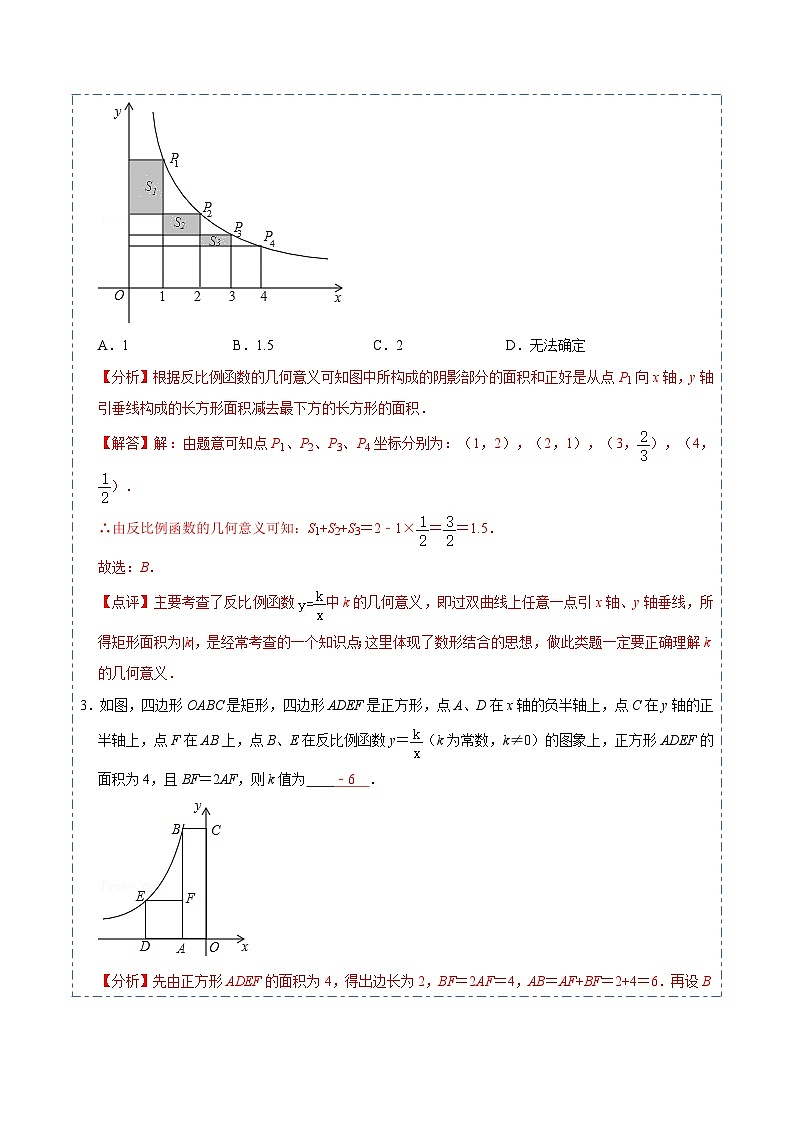
4．如图，A、B两点在双曲线y＝上，分别经过A、B两点向坐标轴作垂线段，已知S阴影＝1.7，则S1+S2等于（ ）
A．4B．4.2C．4.6D．5
【分析】根据反比例函数系数k的几何意义可得S四边形AEOF＝4，S四边形BDOC＝4，根据S1+S2＝S四边形AEOF+S四边形BDOC﹣2×S阴影，可求S1+S2的值．
【解答】解：如图，
∵A、B两点在双曲线y＝上，
∴S四边形AEOF＝4，S四边形BDOC＝4，
∴S1+S2＝S四边形AEOF+S四边形BDOC﹣2×S阴影，
∴S1+S2＝8﹣3.4＝4.6
故选：C．
【点评】本题考查了反比例函数系数k的几何意义，熟练掌握在反比例函数y＝图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
5．如图，在平面直角坐标系中，A（﹣6，0），曲线上每一点到x轴与y轴的距离的乘积都相等，过曲线上横坐标分别为﹣6，﹣4，﹣2的三点B，C，D分别向x轴、y轴作垂线，已知图中的阴影部分是由这些垂线围成的，且其面积是6，则由O，A，C三点围成的三角形的面积为 ．
【分析】根据题意求得S矩形CFGH＝12，S矩形ABGO＝3×12＝36，即可求得CE＝9，然后根据三角形面积公式求得即可．
【解答】解：由反比例函数系数k的几何意义可知：S矩形ABGO＝S矩形CEOH，
∵图中的阴影部分是由这些垂线围成的，且其面积是6，
∴S矩形CFGH＝12，
∴S矩形ABGO＝3×12＝36，
∴HG＝3，OG＝6，
∴CE＝OH＝9，
∴S△OAC＝×6×9＝27．
故答案为27．
【点评】本题考查了反比例函数系数k的几何意义，由几何意义得出S矩形ABGO＝S矩形CEOH是解题的关键．
6．如图，A，B两点在双曲线y＝上，分别经过A，B两点向轴作垂线段，已知阴影小矩形的面积为1，则空白两小矩形面积的和S1+S2＝ 4 ．
【分析】欲求S1+S2，只要求出过A、B两点向x轴、y轴作垂线段与坐标轴所形成的矩形的面积即可，而矩形面积为双曲线y＝的系数k，由此即可求出S1+S2．
【解答】解：∵点A、B是双曲线y＝上的点，分别经过A、B两点向x轴、y轴作垂线段，
则根据反比例函数的图象的性质得两个矩形的面积都等于|k|＝3，
∴S1+S2＝3+3﹣1×2＝4．
故答案为：4
【点评】本题主要考查了反比例函数的图象和性质及任一点坐标的意义，关键是求出过A、B两点向x轴、y轴作垂线段与坐标轴所形成的矩形的面积．
题型2：三角形面积与k的关系
过双曲线() 上任意一点作一坐标轴的垂线，连接该点和原点，所得三角形的面积为.
7．如图，A为反比例函数y＝（k＞0）图象上一点，AB⊥x轴于点B，若S△AOB＝3，则k的值为（ ）
A．1.5B．3C．D．6
【分析】过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S＝|k|．
【解答】解：由于点A是反比例函数y＝图象上一点，则S△AOB＝|k|＝3；
又由于k＞0，则k＝6．
故选：D．
【点评】本题考查了反比例函数系数的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得三角形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
8．如图，等边三角形OAB，点B在x轴正半轴上，S△OAB＝4，若反比例函数y＝（k≠0）图象的一支经过点A，则k的值是（ ）
A．B．C．D．
【分析】根据正三角形的性质以及反比例函数系数k的几何意义，得出S△AOC＝S△AOB＝2＝|k|，即可求出k的值．
【解答】解：如图，过点A作AC⊥OB于点C，
∵△OAB是正三角形，
∴OC＝BC，
∴S△AOC＝S△AOB＝2＝|k|，
又∵k＞0，
∴k＝4，
故选：D．
【点评】本题考查等边三角形的性质，反比例函数系数k的几何意义，掌握等边三角形的性质以及反比例函数系数k的几何意义是正确解答的前提．
9．如图，过反比例函数y＝（x＞0）图象上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连接OA、OB，设AC与OB的交点为E，△AOE与梯形ECDB的面积分别为S1、S2，比较它们的大小，可得（ ）
A．S1＞S2
B．S1＜S2
C．S1＝S2
D．S1、S2的大小关系不能确定
【分析】易得△AOC和△OBD的面积相等，都减去公共部分△OCE的面积可得S1、S2的大小关系．
【解答】解：设点A的坐标为（x，y），点B的坐标为（a，b），
∵A、B在反比例函数y＝上，
∴xy＝2，ab＝2，
∴S△AOC＝xy＝1；S△OBD＝ab＝1．
∴S△AOC＝S△OBD，
∴S△AOC﹣S△OCE＝S△OBD﹣S△OCE，
即S1＝S2．
故选：C．
【点评】考查反比例函数的比例系数的意义；突破点是得到△AOC和△OBD的面积相等．用到的知识点为：在反比例函数图象上的点的横纵坐标的积等于反比例函数的比例系数．
10．如图，点A是反比例函数y＝的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为4，则k的值是（ ）
A．4B．﹣4C．8D．﹣8
【分析】连接OA，如图，利用三角形面积公式得到S△OAB＝S△ABC＝4，再根据反比例函数的比例系数k的几何意义得到|k|＝4，然后去绝对值即可得到满足条件的k的值．
【解答】解：连接OA，如图，
∵AB⊥x轴，
∴OC∥AB，
∴S△OAB＝S△ABC＝4，
而S△OAB＝|k|，
∴|k|＝4，
∵k＜0，
∴k＝﹣8．
故选：D．
【点评】本题考查了反比例函数的比例系数k的几何意义：在反比例函数y＝图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
11.如图所示，点A是反比例函数y＝（x＜0）的图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，若△ABP的面积是2，则k＝ ﹣4 ．
【分析】由于同底等高的两个三角形面积相等，所以△AOB的面积＝△ABP的面积＝2，然后根据反比例函数 y＝中k的几何意义，知△AOB的面积＝|k|，从而确定k的值，求出反比例函数的解析式．
【解答】解：设反比例函数的解析式为 y＝．
∵△AOB的面积＝△ABP的面积＝2，△AOB的面积＝|k|，
∴|k|＝2，
∴k＝±4；
又∵反比例函数的图象的一支位于第二象限，
∴k＜0．
∴k＝﹣4．
故答案为：﹣4．
【点评】本题主要考查了待定系数法求反比例函数的解析式和反比例函数y＝中k的几何意义．这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
12．如图，P1，P2，P3是双曲线上的三点，过这三点分别作y轴的垂线，得到三个△P1A1O，△P2A2O，△P3A3O，设它们的面积分别为S1，S2，S3，则S1，S2，S3的大小关系是（ ）
A．S1＝S2＝S3B．S1＝S3＜S2C．S2＞S3＞S1D．无法确定
【分析】过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S＝|k|．
【解答】解：由题意得：直角三角形面积S是个定值，即S＝|k|．
所以S1＝S2＝S3．
故选：A．
【点评】主要考查了反比例函数中k的几何意义，即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S＝|k|．
题型3：两个象限内三角形的面积与k的关系
13.如图，过y轴上任意一点P，作x轴的平行线，分别与反比例函数y＝﹣和y＝的图象交于A点和B点，若C为x轴上任意一点，连接AC，BC，则△ABC的面积为 3 ．
【分析】先设P（0，b），由直线AB∥x轴，则A，B两点的纵坐标都为b，而A，B分别在反比例函数y＝﹣和y＝的图象上，可得到A点坐标为（﹣，b），B点坐标为（，b），从而求出AB的长，然后根据三角形的面积公式计算即可．
【解答】解：设P（0，b），
∵直线AB∥x轴，
∴A，B两点的纵坐标都为b，而点A在反比例函数y＝﹣的图象上，
∴当y＝b，x＝﹣，即A点坐标为（﹣，b），
又∵点B在反比例函数y＝的图象上，
∴当y＝b，x＝，即B点坐标为（，b），
∴AB＝﹣（﹣）＝，
∴S△ABC＝•AB•OP＝••b＝3．
故答案为：3．
【点评】本题考查的是反比例函数系数k的几何意义，即在反比例函数y＝的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，且保持不变．
14.如图，在平面直角坐标系中，过原点O的直线交反比例函数y＝图象于A，B两点，BC⊥y轴于点C，△ABC的面积为6，则k的值为 ﹣6 ．
【分析】根据反比例函数的对称性和反比例函数系数k的几何意义，可求出S△BOC＝S△ABC＝＝|k|，再根据图象所在的象限确定k的值即可．
【解答】解：由对称性可知，OA＝OB，
∴S△AOC＝S△BOC＝S△ABC，
∵BC⊥y轴，△ABC的面积为6，
∴S△BOC＝S△ABC＝＝|k|，
又∵k＜0，
∴k＝﹣6，
故答案为：﹣6．
【点评】本题考查反比例函数系数k的几何意义，掌握反比例函数系数k的几何意义以及反比例函数的性质是正确解答的关键．
15．如图，两个反比例函数y＝和y＝﹣的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则△PAB的面积为 ．
【分析】设P的坐标是（a，），推出A的坐标和B的坐标，求出∠APB＝90°，求出PA、PB的值，根据三角形的面积公式求出即可．
【解答】解：∵点P在y＝上，
∴|xp|×|yp|＝|k|＝1，
∴设P的坐标是（a，）（a为正数），
∵PA⊥x轴，
∴A的横坐标是a，
∵A在y＝﹣上，
∴A的坐标是（a，﹣），
∵PB⊥y轴，
∴B的纵坐标是，
∵B在y＝﹣上，
∴代入得：＝﹣，
解得：x＝﹣2a，
∴B的坐标是（﹣2a，），
∴PA＝|﹣（﹣）|＝，PB＝|a﹣（﹣2a）|＝3a，
∵PA⊥x轴，PB⊥y轴，x轴⊥y轴，
∴PA⊥PB，
∴△PAB的面积是：PA×PB＝××3a＝
故答案为：．
【点评】本题考查了反比例函数和三角形面积公式的应用，关键是能根据P点的坐标得出A、B的坐标，本题具有一定的代表性，是一道比较好的题目．
16．如图，A、B是函数y＝的图象上关于原点对称的任意两点，BC∥x轴，AC∥y轴，△ABC的面积记为S，则S＝ 4 ．
【分析】连接OC，设AC与x轴交于点D，BC与y轴交于点E．首先由反比例函数y＝的比例系数k的几何意义，可知△AOD的面积等于|k|，再由A、B两点关于原点对称，BC∥x轴，AC∥y轴，可知S△AOC＝2×S△AOD，S△ABC＝2×S△AOC，从而求出结果．
【解答】解：如图，连接OC，设AC与x轴交于点D，BC与y轴交于点E．
∵A、B两点关于原点对称，BC∥x轴，AC∥y轴，
∴AC⊥x轴，AD＝CD，OA＝OB，
∴S△COD＝S△AOD＝×2＝1，
∴S△AOC＝2，
∴S△BOC＝S△AOC＝2，
∴S△ABC＝S△BOC+S△AOC＝4．
故答案为：4．
【点评】本题主要考查了三角形一边上的中线将三角形的面积二等分及反比例函数的比例系数k的几何意义：反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系，即S＝|k|．
17．如图，正比例函数y＝kx（k＞0）与反比例函数的图象相交于A，C两点，过A作x轴的垂线交x轴于B，连接BC，则△ABC的面积为 1 ．
【分析】过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，点A，C关于原点对称，则△ABC的面积为△AOB面积的2倍，即S＝|k|．
【解答】解：因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，
即S＝|k|，
依题意有S△ABC＝2S△AOB＝2××|k|＝1．
故答案为：1．
【点评】此题主要考查了反比例函数y＝中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得三角形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
18．如图，A、B是反比例函数y＝的图象上关于原点O对称的任意两点，过点A作AC⊥x轴于点C，连接BC，则△ABC的面积为（ ）
A．1B．2C．3D．4
【分析】根据反比例函数的性质可知△AOC的面积为1，由于对称性可知：△AOC与△BOC的面积相等，从而可求出答案．
【解答】解：由题意可知：△AOC的面积为1，
∵A、B关于原点O对称，
∴△AOC与△BOC的面积相等，
∴S△ABC＝2S△AOC＝2，
故选：B．
【点评】本题考查反比例函数，解题的关键是熟练运用反比例函数的性质，本题属于基础题型．
19．如图，点A（m，1），B（2，n）在双曲线y＝（k≠0）上，连接OA，OB．若S△ABO＝8，则k的值是（ ）
A．﹣12B．﹣8C．﹣6D．﹣4
【分析】过A作y轴的垂线，过B作x轴的垂线，交于点C，连接OC，依据S△ABC﹣S△ACO﹣S△BOC＝8，即可得到k的值．
【解答】解：过A作y轴的垂线，过B作x轴的垂线，交于点C，连接OC，
设A（k，1），B（2，k），则AC＝2﹣k，BC＝1﹣k，
∵S△ABO＝8，
∴S△ABC﹣S△ACO﹣S△BOC＝8，
即（2﹣k）（1﹣k）﹣（2﹣k）×1﹣（1﹣k）×2＝8，
解得k＝±6，
∵k＜0，
∴k＝﹣6，
故选：C．
【点评】本题考查了反比例函数与一次函数的交点问题，待定系数法求函数的解析式，正确理解△AOB的面积的计算方法是关键．
20．如图，直线y＝kx（k＞0）与双曲线y＝交于A，B两点，BC⊥x轴于C，连接AC交y轴于D，下列结论：①A、B关于原点对称；②△ABC的面积为定值；③D是AC的中点；④S△AOD＝．其中正确结论的个数为（ ）
A．1个B．2个C．3个D．4个
【分析】根据反比例函数的对称性、函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S＝|k|及三角形中位线的判定作答．
【解答】解：①反比例函数与正比例函数若有交点，一定是两个，且关于原点对称，所以正确；
②根据A、B关于原点对称，S△ABC为即A点横纵坐标的乘积，为定值1，所以正确；
③因为AO＝BO，OD∥BC，所以OD为△ABC的中位线，即D是AC中点，所以正确；
④在△ADO中，因为AD和y轴并不垂直，所以面积不等于k的一半，即不会等于，所以错误．
因此正确的是：①②③，
故选：C．
【点评】此题主要考查了反比例函数中比例系数k的几何意义，难易程度适中．
21．如图所示，过y轴正半轴上的任意一点P，作x轴的平行线，分别与反比例函数的图象交于点A和点B，若点C是x轴上任意一点，连接AC、BC，则△ABC的面积为 3 ．
【分析】先设P（0，b），由直线AB∥x轴，则A，B两点的纵坐标都为b，而A，B分别在反比例函数y＝﹣和y＝的图象上，可得到A点坐标为（﹣，b），B点坐标为（，b），从而求出AB的长，然后根据三角形的面积公式计算即可．
【解答】解：设P（0，b），
∵直线AB∥x轴，
∴A，B两点的纵坐标都为b，而点A在反比例函数y＝﹣的图象上，
∴当y＝b，x＝﹣，
即A点坐标为（﹣，b），
又∵点B在反比例函数y＝的图象上，
∴当y＝b，x＝，
即B点坐标为（，b），
∴AB＝﹣（﹣）＝，
∴S△ABC＝•AB•OP＝••b＝3．
故答案为：3．
【点评】本题考查的是反比例函数系数k的几何意义，即在反比例函数y＝的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是，且保持不变．
题型4：两个及以上反比例函数的面积问题
21．两个反比例函数C1：和C2：在第一象限内的图象如图所示，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，则四边形PAOB的面积为（ ）
A．1B．2C．3D．4
【分析】根据反比函数比例系数k的几何意义得到S△AOC＝S△BOD＝k|，S矩形PCOD＝|2|＝2，然后利用矩形面积分别减去两个三角形的面积即可得到四边形PAOB的面积．
【解答】解：∵PC⊥x轴，PD⊥y轴，
∴S△AOC＝S△BOD＝|k|＝，S矩形PCOD＝|2|＝2，
∴四边形PAOB的面积＝2﹣2•＝1．
故选：A．
【点评】本题考查了反比函数比例系数k的几何意义：在反比例函数y＝图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
22．双曲线C1：y＝﹣（k≠0）和C2：y＝﹣的图象如图所示，点A是C1上一点，分别过点A作AB⊥x轴，AC⊥y轴，垂足分别为点B、点C，AB与C2交于点D，若△AOD的面积为2，则k的值为（ ）
A．3B．5C．﹣3D．﹣5
【分析】根据反比例函数k值的几何意义及其基本模型计算即可．
【解答】解：S△AOD＝S△AOB﹣S△DOB，
∴，
∴|k|＝5，
∵反比例函数位于第二象限，
∴﹣k＜0，则k＞0，
∴k＝5
故选：B．
【点评】本题考查反比例函数k值的几何意义，理解反比例函数k值的几何意义是正确解答关键．
23．如图，两个反比例函数y＝和y＝在第一象限内的图象分别是C1和C2，设点P在C1上，PA⊥x轴于点A，交C2于点B，则△POB的面积为（ ）
A．1B．2C．4D．无法计算
【分析】根据反比例函数y＝（k≠0）系数k的几何意义得到S△POA＝×4＝2，S△BOA＝×2＝1，然后利用S△POB＝S△POA﹣S△BOA进行计算即可．
【解答】解：∵PA⊥x轴于点A，交C2于点B，
∴S△POA＝×4＝2，S△BOA＝×2＝1，
∴S△POB＝2﹣1＝1．
故选：A．
【点评】本题考查了反比例函数y＝（k≠0）系数k的几何意义：从反比例函数y＝（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|．
24．如图，两个反比例函数y＝和y＝在第一象限内的图象依次是C1和C2，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，若四边形PAOB的面积为5，则k＝ ．
【分析】根据反比例函数系数k的几何意义得到S矩形PCOD＝k，S△AOC＝S△BOD＝，然后利用四边形PAOB的面积＝S矩形PCOD﹣S△AOC﹣S△BOD进行计算．
【解答】解：∵PC⊥x轴，PD⊥y轴，
∴S矩形PCOD＝k，S△AOC＝S△BOD＝＝，
∴四边形PAOB的面积＝S矩形PCOD﹣S△AOC﹣S△BOD＝k﹣﹣＝5．
解得k＝8．
故答案是：8．
【点评】主要考查了反比例函数y＝中k的几何意义，即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S＝|k|．
25．如图，函数y＝（x＞0）和（x＞0）的图象分别是l1和l2．设点P在l2上，PA∥y轴交l1于点A，PB∥x轴交l1于点B，△PAB的面积为 ．
【分析】设点P（x，），则点B（，），A（x，），得到BP，AP的长，最后求得△ABP的面积．
【解答】解：设点P（x，），则点B（，），A（x，），
∴BP＝x﹣＝，AP＝﹣＝，
∴S△ABP＝＝，
故答案为：．
【点评】本题考查了反比例函数的图象上点的坐标特征，直角三角形的面积，解题的关键是熟知反比例函数图象上点的坐标的特征．
26．反比例函数，（n＜0）的图象如图所示，点P为x轴上不与原点重合的一动点，过点P作AB∥y轴，分别与y1、y2交于A、B两点．
（1）当n＝﹣10时，求S△OAB；
（2）延长BA到点D，使得DA＝AB，求在点P整个运动过程中，点D所形成的函数图象的表达式．（用含有n的代数式表示）．
【分析】（1）当n＝﹣10时，S△BOP＝×|﹣10|＝5，S△AOP＝×|8|＝4，即可得S△OAB＝9；
（2）设P（m，0），则A（m，），B（m，），AB＝|﹣|，分两种情况：①当m＞0时，AB＝＝AD，D（m，），设x＝m，y＝，则xy＝16﹣n，可得y＝，②当m＜0时，可得y＝．
【解答】解：（1）当n＝﹣10时，y2＝﹣，
∴S△BOP＝×|﹣10|＝5，
∵A在y＝的图象上，
∴S△AOP＝×|8|＝4，
∴S△OAB＝S△BOP+S△AOP＝9，
答：S△OAB＝9；
（2）设P（m，0），则A（m，），B（m，），
∴AB＝|﹣|，
①当m＞0时，AB＝＝AD，
∴DP＝AD+AP＝+＝，
∴D（m，），
设x＝m，y＝，则xy＝16﹣n，
∴y＝，即点D所形成的函数图象的表达式为y＝，
②当m＜0时，AB＝，
同理可得y＝，
综上所述，点D所形成的函数图象的表达式为y＝．
【点评】本题考查反比例函数图象及性质，解题的关键是分类思想的应用．
27．双曲线与在第一象限内的图象如图所示，作一条平行于y轴的直线分别交双曲线于A、B两点，连接OA、OB，则△AOB的面积为（ ）
A．1B．2C．3D．4
【分析】如果设直线AB与x轴交于点C，那么△AOB的面积＝△AOC的面积﹣△COB的面积．根据反比例函数的比例系数k的几何意义，知△AOC的面积＝5，△COB的面积＝3，从而求出结果．
【解答】解：设直线AB与x轴交于点C．
∵AB∥y轴，
∴AC⊥x轴，BC⊥x轴．
∵点A在双曲线y＝的图象上，
∴△AOC的面积＝×10＝5．
∵点B在双曲线y＝的图象上，
∴△COB的面积＝×6＝3．
∴△AOB的面积＝△AOC的面积﹣△COB的面积＝5﹣3＝2．
故选：B．
【点评】本题主要考查反比例函数的比例系数k的几何意义．反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系，即S＝|k|．
28．双曲线C1：y＝和C2：y＝如图所示，点A是C1上一点，分别过点A作AB⊥x轴，AC⊥y轴，垂足分别为点B、点C，AB，AC与C2分别交于点D、点E，若四边形ADOE的面积为4，则k1﹣k2＝ ﹣4 ．
【分析】由反比例函数k的几何意义得到S△OBD＝﹣k2，S△OCE＝﹣k2，S矩形ABOC＝﹣k1，根据S矩形ABOC﹣S△OBD﹣S△OCE＝S四边形ADOE即可求出k1﹣k2．
【解答】解：∵D，E在反比例函数y＝的图象上，且图象在第二象限，
∴S△OBD＝OB•BD＝﹣k2，S△OCE＝OC•CE＝﹣k2，
∵A在反比例函数y＝的图象上，且图象在第二象限，
∴S矩形ABOC＝OB•OC＝﹣k1
∴k1﹣k2＝﹣[﹣k1﹣（﹣k2）]＝﹣（S矩形ABOC﹣S△OBD﹣S△OCE）＝﹣S四边形ADOE＝﹣4，
故答案为：﹣4．
【点评】本题主要考查了反比例函数k的几何意义，掌握反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的|k|值是解决问题的关键．