初中数学人教版九年级下册第二十八章 锐角三角函数28.1 锐角三角函数巩固练习

这是一份初中数学人教版九年级下册第二十八章 锐角三角函数28.1 锐角三角函数巩固练习，文件包含281锐角三角函数讲+练10大题型原卷版docx、281锐角三角函数讲+练10大题型解析版docx等2份试卷配套教学资源，其中试卷共48页， 欢迎下载使用。


一、单选题
1．如果把一个锐角三角形三边的长都扩大为原来的两倍，那么锐角A的余切值（ ）
A．扩大为原来的两倍B．缩小为原来的 12
C．不变D．不能确定
【答案】C
【解析】【解答】因为△ABC三边的长度都扩大为原来的2倍所得的三角形与原三角形相似，
所以锐角A的大小没改变，所以锐角A的余切值也不变.
故答案为：C.
【分析】根据相似三角形的性质可知三角形的边长扩大，角度不会发生改变，即锐角A的大小没改变，所以锐角A的余切值也不变.
2．如图， ∠α 的顶点位于正方形网格的格点上，若 tanα=23 ，则满足条件的 ∠α 是（ ）
A．B．
C．D．
【答案】B
【解析】【解答】A. tanα=32 ，故该选项不符合题意，
B. tanα=23 ，故该选项符合题意，
C. tanα=12 ，故该选项不符合题意，
D. tanα=13 ，故该选项不符合题意，
故答案为：B.
【分析】根据网格特点分别求出各选项中tanα的值，然后判断即可.
3．cs60°的值等于（ ）
A．1B．12C．22D．32
【答案】A
【解析】【解答】解：cs60°= 12
故答案为：A.
【分析】由特殊角的三角函数值可知。
4．如图，△ABC的三个顶点在正方形网格的格点上，则tan∠A的值是（ ）
A．65B．56C．2102D．31020
【答案】A
【解析】【解答】解：利用三角函数的定义可知tan∠A= 65 ．
故选A．
【分析】根据三角函数的定义即可求出tan∠A的值．
5．在Rt△ABC中，∠C=90°，若sinA= 23 ， 则tanB=（ ）
A．355B．53C．255D．52
【答案】D
【解析】【解答】解：∵sinA=BCAC=23，
∴设BC=2x，AB=3x，
由勾股定理得：AC=AB2−BC2=5x，
∴tanB=ACBC=5x2x=52
故答案为：D.
【分析】设BC=2x，AB=3x，由勾股定理求得AC=5x，代入tanB=ACBC求出即可.
6．如图，在△ABC中，∠BAC=90°，D是BC的中点，若AB=8，AD=5，则sinB等于（ ）
A．35B．45C．34D．58
【答案】A
【解析】【解答】解：∵在△ABC中，∠BAC=90°，D是BC的中点，
∴AD是Rt△ABC斜边BC上的中线，
∴BC=2AD=2×5=10，
∵AB=8，
∴AC=BC2−AB2=102−82=6，
∴sinB=ACBC=610=35．
故答案为：A．
【分析】先利用直角三角形斜边上中线的性质可得BC=2AD=2×5=10，利用勾股定理求出AC的长，再利用正弦的定义可得sinB=ACBC=610=35。
二、填空题
7．计算：4tan45°＝ ．
【答案】4
【解析】【解答】解：4tan45°=4×1=4．
故答案为：4．
【分析】利用特殊角的锐角三角函数值计算求解即可。
8．要使二次根式 x−sin30° 有意义，则 x 的取值范围为
【答案】x≥12
【解析】【解答】解：二次根式 x−sin30° 被开方数为 x−sin30°
∴x−sin30°≥0
又∵sin30°=12
∴x−12≥0 ，解得 x≥12
故答案为： x≥12 .
【分析】二次根式有意义的条件：被开方数为非负数，再结合特殊角三角函数值解答即可.
9．如图，已知梯形ABCD中，AB∥CD，AB⊥BC，且AD⊥BD，若CD=1，BC=3，那么∠A的正切值为 ．
【答案】13
【解析】【解答】解：∵AB∥CD，AB⊥BC，
∴DC⊥BC，∠ABC=90°，
∴∠C=90°，
∵AD⊥BD，
∴∠ADB=90°，
∴∠DBC+∠ABD=∠A+∠ABD=90°，
∴∠A=∠DBC，
∵CD=1，BC=3，
∴∠A的正切值为tanA=tan∠DBC= DCBC = 13 ，
故答案为： 13 ．
【分析】首先根据同角的余角相等可得∠A=∠DBC，在直角三角形BCD中求出tan∠DBC的值即为∠A的正切值。
10．如图，△ABC中，∠C＝90°，BC＝6，∠ABC的平分线与线段AC交于点D，且有AD＝BD，点E是线段AB上的动点（与A、B不重合），连结DE，当△BDE是等腰三角形时，则AE的长为 .
【答案】8 或 12−43
【解析】【解答】解：∵△ABC中BD平分∠ABC，
∴∠CBD=∠ABD，
∵BD=AD，
∴∠ABD=∠BAD，
∴∠CBD=∠ABD=∠BAD，
∵∠ACB=90°，
∴∠CBD+∠ABD+∠BAD=90°，
∴∠CBD=∠ABD=∠BAD=30°，
∵BC=6，
∴AB=2BC=12， AC=AB2−BC2=122−62=63 ，
BD=BCcs30°=632=43 ，
∴AD=BD=43 ，
CD=AC−AD=63−43=23 ；
（1）当 BE=BD=43 时，如图所示：
AE=AB−BE=12−43 ；
（2）当BE=DE时，如图所示：
∵BE=DE，
∴∠EDB=∠ABD=30°，
∴∠AED=∠EDB+∠ABD=60°，
∴∠ADE=180°-∠AED-∠A=180°-60°-30°=90°，
∴△ADE为直角三角形，
∴AE=ADsin∠AED=43sin60°=8 ；
（3）当BD=DE时，点E与点A重合，不符合题意；
综上分析可知，AE的值为 12−43 或8.
故答案为：12−43 或8.
【分析】根据角平分线的概念得∠CBD=∠ABD，根据等腰三角形的性质得∠ABD=∠BAD，则∠CBD=∠ABD=∠BAD，结合内角和定理得∠CBD=∠ABD=∠BAD=30°，根据含30°角的直角三角形的性质可得AB=2BC=12，利用勾股定理求出AC，根据三角函数的概念得BD，然后根据CD=AC-AD求出CD；当BE=BD=43时，根据AE=AB-BE可得AE；当BE=DE时，∠EDB=∠ABD=30°，由外角的性质可得∠AED=∠EDB+∠ABD=60°，利用内角和定理可得∠ADE=90°，然后根据三角函数的概念进行计算；当BD=DE时，点E与点A重合，不符合题意，据此解答.
11．（3.14﹣π）0+2cs45°﹣|1﹣ 2 |+（ 12 ）﹣1= ．
【答案】4
【解析】【解答】解：原式=1+2× 22 ﹣ 2 +1+2=4，
故答案为：4
【分析】此题的运算顺序是：先算乘方运算，再算乘除运算，最后算加减法。易错点：|1﹣2 |=2-1≠1-2，（12）-1=2≠-2。
三、解答题
12．计算：（ 12 ）﹣2+（π﹣3.14）0﹣| 3−2 |﹣2cs30°．
【答案】解：原式=4+1﹣（2﹣ 3 ）﹣2× 32 =5﹣2+ 3 ﹣ 3 =3
【解析】【分析】本题考查实数的运算能力，解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式等考点的运算．本题涉及零指数幂、负整数指数幂、特殊角的三角函数值、二次根式化简四个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则计算．注意：负指数为正指数的倒数；任何非0数的0次幂等于1；二次根式的化简是根号下不能含有分母和能开方的数．
13．先化简，再求代数式x−4x2−9÷(1−1x−3)的值，其中x=2sin45°−3tan60°．
【答案】解：原式=x−4(x+3)(x−3)÷(x−3x−3−1x−3)
=x−4(x+3)(x−3)⋅x−3x−4
=1x+3；
∵x=2sin45°−3tan60°
=2×22−3×3
=2−3，
∴原式=1x+3
=12−3+3
=22．
【解析】【分析】先利用分式的混合运算化简，再求出x的值，最后将x的值代入计算即可。
四、综合题
14．如图，⊙O的直径AB=10，弦AC=6，∠ACB的平分线交⊙O于D，过点D作DE∥AB交CA的延长线于点E，连接AD，BD．
（1）由AB，BD， AD 围成的曲边三角形的面积是 ；
（2）求证：DE是⊙O的切线；
（3）求线段DE的长．
【答案】（1）252+25π4
（2）证明：由（1）知∠AOD=90°，即OD⊥AB．
∵DE∥AB，∴OD⊥DE，
∴DE是⊙O的切线；
（3）解：∵AB=10、AC=6，∴BC= AB2−AC2 =8． 过点A作AF⊥DE于点F，
则四边形AODF是正方形，∴AF=OD=FD=5，∴∠EAF=90°﹣∠CAB=∠ABC，
∴tan∠EAF=tan∠CBA，
∴EFAF=ACBC ，即 EF5=68 ， ∴EF= 154 ，
∴DE=DF+EF= 154 +5= 354 ．
【解析】【解答】解：（1）如图，连接OD．
∵AB是直径，且AB=10，
∴∠ACB=90°，AO=BO=DO=5．
∵CD平分∠ACB，∴∠ABD=∠ACD= 12 ∠ACB=45°，
∴∠AOD=90°，则曲边三角形的面积是
S扇形AOD+S△BOD= 90π×52360 + 12 ×5×5= 252+25π4 ．
故答案为 252+25π4 ；
【分析】（1）连接OD，由AB是直径知∠ACB=90°，结合CD平分∠ACB知∠ABD=∠ACD=45°，从而知∠AOD=90°，根据曲边三角形的面积=S扇形AOD+S△BOD可得答案；
（2）由∠AOD=90°，即OD⊥AB，根据DE∥AB可得OD⊥DE，即可得证；
（3）勾股定理求得BC=8，作AF⊥DE知四边形AODF是正方形，即可得DF=5，由∠EAF=90°﹣∠CAB=∠ABC知tan∠EAF=tan∠CBA，即 EFAF=ACBC ，求得EF的长即可得．
15．如图，在平行四边形ABCD中，以A为圆心，AB长为半径画弧交AD于点F；再分别以B，F为圆心，大于12BF的长为半径作弧，两弧交于点P；连接AP并延长交BC于点E，连接EF．
（1）求证：四边形ABEF是菱形；
（2）若菱形ABEF的周长为4，AE=3，则请直接写出csC的大小为 ．
【答案】（1）证明：由尺规作图可知，AB=AF，AE是∠BAF的角平分线，
∴∠EAB＝∠EAF，
在△AEB和△AEF中，
AB=AF∠BAE=∠FAEAE=AE，
∴△AEB≌△AEF（SAS），
∴BE=EF，
∵AD∥BC，
∴∠BEA=∠FAE，
∴∠AEB＝∠EAB，
∴BE＝AB，
∵EF=BE，AB=AF，
∴AB=BE=EF=AF，
∴四边形ABEF是菱形；
（2）12
【解析】【解答】解： (2)连接BF，交AE于G，如图所示：
∵菱形ABEF的周长为4，
∴AB=BE=EF=AF=1，
∵GA＝12AE=32，AE⊥BF，
在Rt△AGB中，GF=AF2−AG2=12−(32)2=12，
∴∠FAG＝30°，
∴∠BAF＝2∠BAG＝60°，
∴在▱ABCD中，∠C＝∠BAF＝60°，
∴csC=cs60°=12，
故答案为：12．
【分析】（1）利用菱形的判定方法求解即可；
（2）连接BF，交AE于G，先求出GF=AF2−AG2=12−(32)2=12，再求出∠C＝∠BAF＝60°，最后利用余弦的定义可得答案。
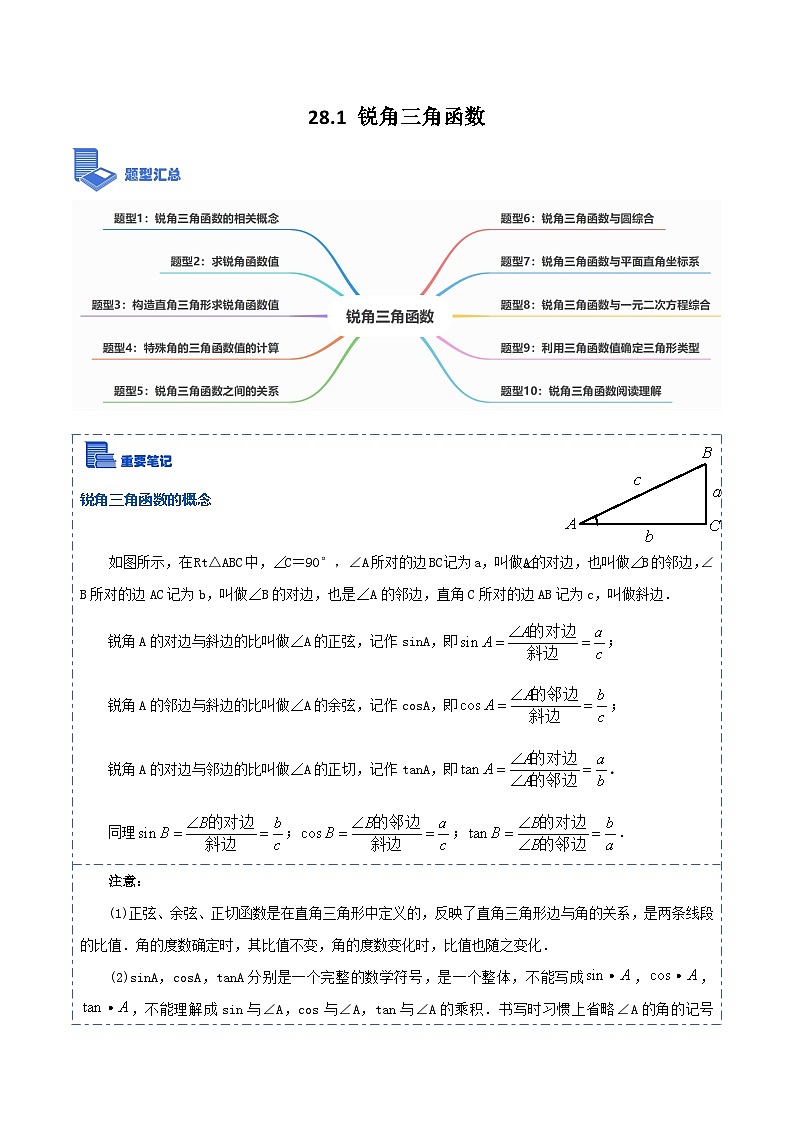
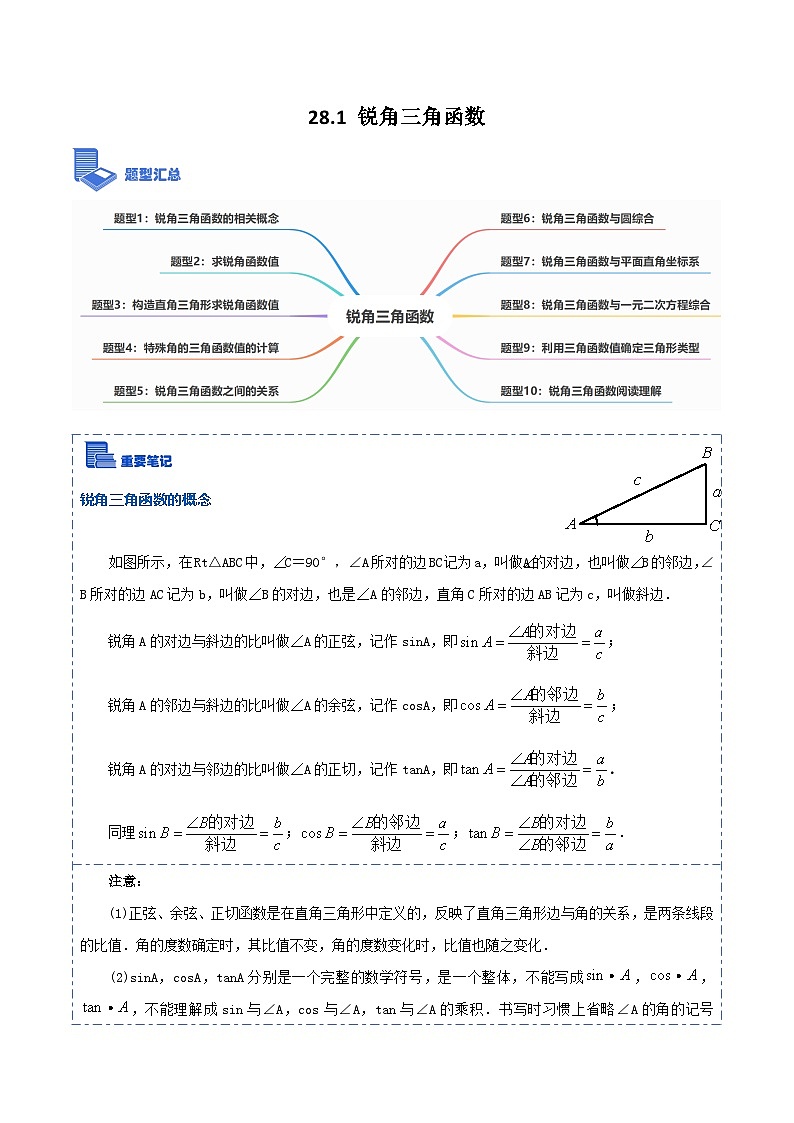
锐角三角函数的概念
如图所示，在Rt△ABC中，∠C＝90°，∠A所对的边BC记为a，叫做∠A的对边，也叫做∠B的邻边，∠B所对的边AC记为b，叫做∠B的对边，也是∠A的邻边，直角C所对的边AB记为c，叫做斜边．
锐角A的对边与斜边的比叫做∠A的正弦，记作sinA，即；
锐角A的邻边与斜边的比叫做∠A的余弦，记作csA，即；
锐角A的对边与邻边的比叫做∠A的正切，记作tanA，即.
同理；；．
注意：
(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化．
(2)sinA，csA，tanA分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin与∠A，cs与∠A，tan与∠A的乘积．书写时习惯上省略∠A的角的记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成“tanAEF”；另外，、、常写成、、．
(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．
(4)由锐角三角函数的定义知：当角度在0°<∠A<90°间变化时，，，tanA＞0．
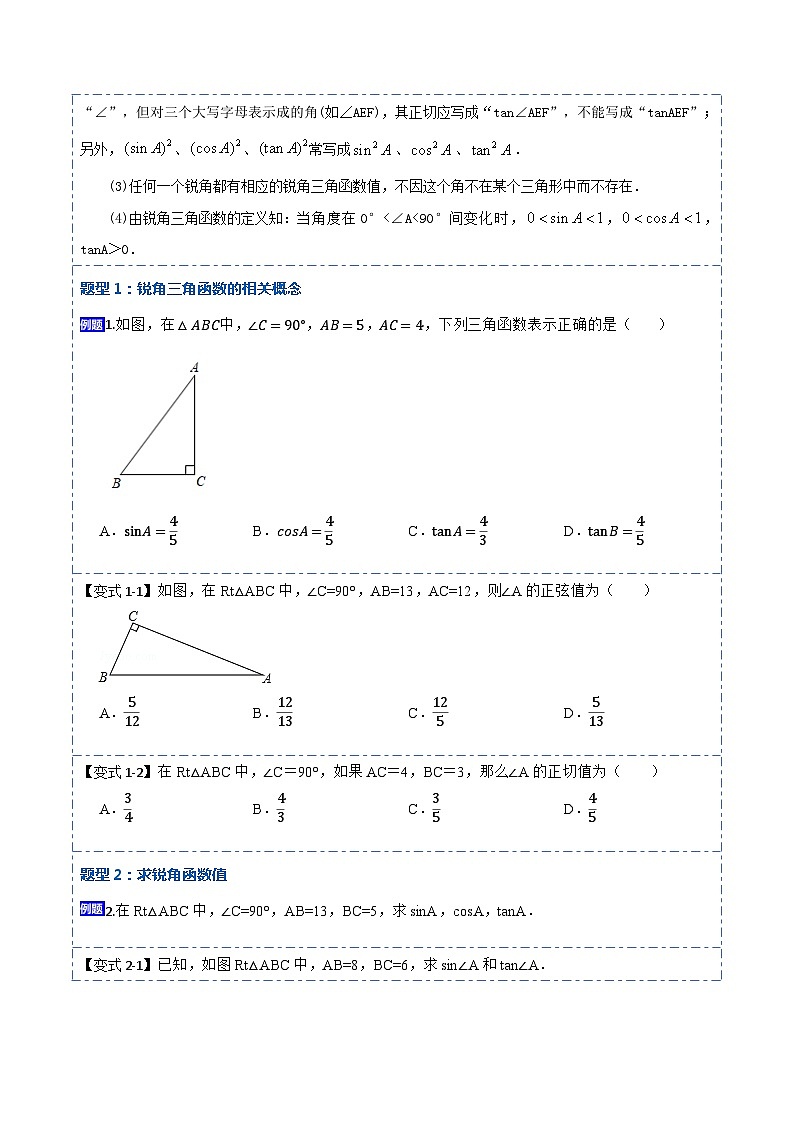
题型1：锐角三角函数的相关概念
1.如图，在△ABC中，∠C=90°，AB=5，AC=4，下列三角函数表示正确的是（ ）
A．sinA=45B．csA=45C．tanA=43D．tanB=45
【答案】B
【解析】【解答】∵∠C=90°，AB=5，AC=4
∴BC=AB2−AC2=52−42=3
∴sinA=BCAB=35， A不符合题意；
∴csA=ACAB=45，B符合题意；
∴tanA=BCAC=34， C不符合题意；
∴tanB=ACBC=43， D不符合题意；
故答案为：B．
【分析】利用正弦、余弦和正切的定义逐项判断即可。
【变式1-1】如图，在Rt△ABC中，∠C=90°，AB=13，AC=12，则∠A的正弦值为（ ）
A．512B．1213C．125D．513
【答案】D
【解析】【解答】在Rt△ABC中，∠C=90°，AB=13，AC=12，
∴BC= AB2−AC2 =5，
∴sinA= BCAB = 513 ，
故答案为：D.
【分析】在Rt△ABC中，利用勾股定理求出BC=15，根据锐角三角函数的定义可得sinA= BCAB，由此计算即可.
【变式1-2】在Rt△ABC中，∠C＝90°，如果AC＝4，BC＝3，那么∠A的正切值为（ ）
A．34B．43C．35D．45
【答案】A
【解析】【解答】解：在Rt△ABC中,∠C=90°,AC=4,BC=3,∴ tanA= BCAC=34 .
故答案为：A.
【分析】根据正切函数的定义tan∠A=∠A的对边∠A的邻边即可直接得出答案.
题型2：求锐角函数值
2.在Rt△ABC中，∠C=90°，AB=13，BC=5，求sinA，csA，tanA．
【答案】解：由勾股定理得，AC= AB2−BC2 = 132−52 =12，
sinA= BCAB = 513 ，
csA= ACAB = 1213 ，
tanA= BCAC = 512 ．
【解析】【分析】利用勾股定理列式求出AC，然后根据锐角的三角函数列式即可．
【变式2-1】已知，如图Rt△ABC中，AB=8，BC=6，求sin∠A和tan∠A．
【答案】解：在Rt△ABC中，由勾股定理，得
AC= AB2+BC2 =10，
sin∠A= BCAC = 610 = 35 ；
tan∠A= ACAB = 68 = 34
【解析】【分析】根据勾股定理，可得AC的长，根据在直角三角形中，锐角的正弦为对边比斜边，正切为对边比邻边，可得答案．
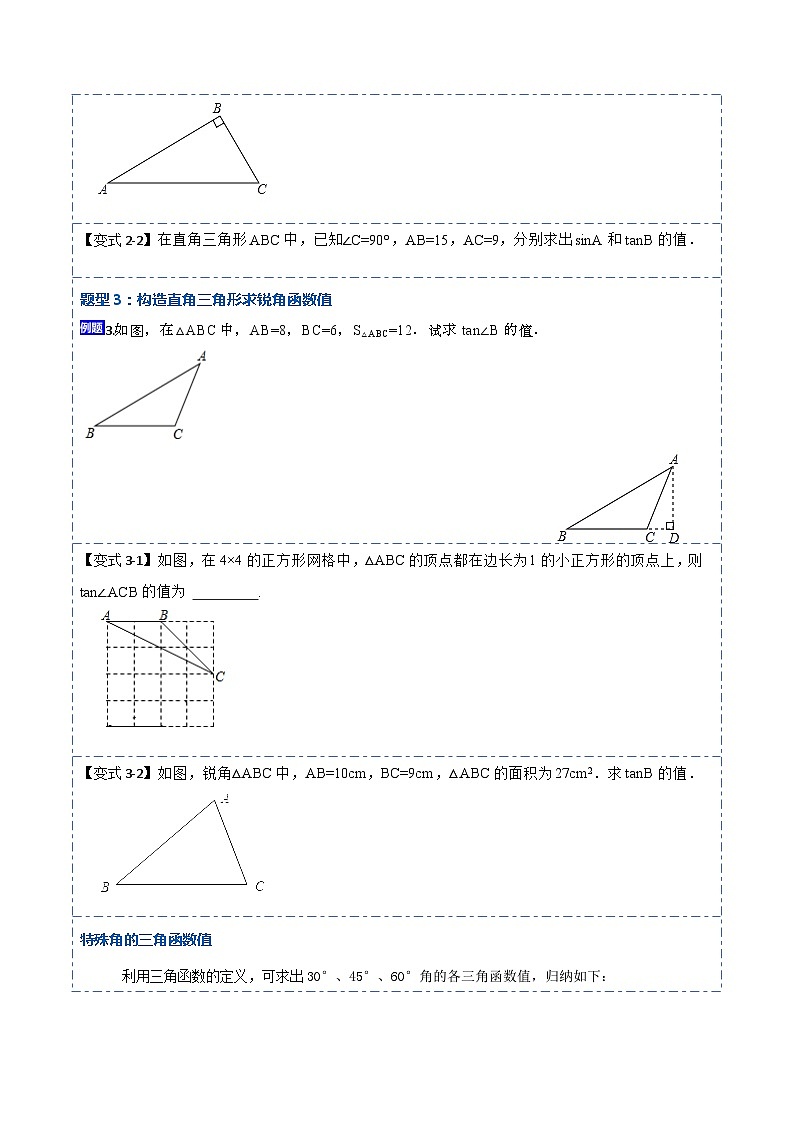
【变式2-2】在直角三角形ABC中，已知∠C=90°，AB=15，AC=9，分别求出sinA和tanB的值．
【答案】解：如图，∵∠C=90°，AB=15，AC=9，
∴BC=AB2−AC2=12，
∴sinA=BCAB=45，tanB=ACBC=43．
【解析】【分析】利用勾股定理得出BC的长，再利用锐角三角函数关系得出答案．
题型3：构造直角三角形求锐角函数值
3.如图，在△ABC中，AB=8，BC=6，S△ABC=12．试求tan∠B的值．
【分析】过点A作AD⊥BC的延长线于D，利用三角形的面积求出AD，再利用勾股定理列式求出BD，然后根据锐角的正切值等于对边比邻边列式计算即可得解．
【解答】解：如图，过点A作AD⊥BC的延长线于D，
【点评】本题考查了锐角三角函数的定义，勾股定理，作出辅助线构造成直角三角形是解题的关键．
【变式3-1】如图，在4×4的正方形网格中，△ABC的顶点都在边长为1的小正方形的顶点上，则tan∠ACB的值为 .
【答案】13
【解析】【解答】解：过点B作BD⊥AC于点D，如图，
由勾股定理得， AC=22+42=25
根据等积关系得， 12×AB×CE=12×AC×BD
∴BD=AB·CEAC=2×225=255
由勾股定理得， AD=AB2−BD2=22−(255)2=455
∴CD=AC−AD=25−455=655
∴tan∠ACB=BDCD=255655=13
故答案为： 13.
【分析】过点B作BD⊥AC于点D，如图，根据勾股定理求出AC=2 5，利用△ABC的面积求出BD的长，再利用勾股定理求出AD，从而求出CD=AC=AD的长，根据tan∠ACB=BDCD 即可求解.
【变式3-2】如图，锐角△ABC中，AB=10cm，BC=9cm，△ABC的面积为27cm2．求tanB的值．
【答案】解：过点A作AH⊥BC于H，∵S△ABC=27，∴12×9×AH=27 ，∴AH=6，∵AB=10，∴BH= AB2−AH2 = 102−62 =8，∴tanB= AHBH = 68 = 34 ．
【解析】【分析】 过点A作AH⊥BC于H，根据△ABC的面积为27可求出AH的长，在直角三角形ABH中用勾股定理求出BH的长，则tanB的值可求。
特殊角的三角函数值
利用三角函数的定义，可求出30°、45°、60°角的各三角函数值，归纳如下：
锐角
30°
45°
1
60°

注意：
(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．
(2)仔细研究表中数值的规律会发现：
、、的值依次为、、，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：
①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)；
②余弦值随锐角度数的增大(或减小)而减小(或增大)．
题型4：特殊角的三角函数值的计算
4.计算：
（1）sin45°cs45°+4tan30°sin60° ；
（2）cs60°−2sin245°+23tan60°−sin30° .
（3）sin60°+3tan30°·cs60°1−2ct45°·ct30°．
【答案】（1）解： sin45°cs45°+4tan30°sin60°
=22×22+4×33×32
=12+2
=52.
（2）解：cs60°−2sin245°+23tan260°−sin30° .
=12 -2×222+23×32-12
=12-1+2-12
=1.
（3）sin60°+3tan30°·cs60°1−2ct45°·ct30°．
【答案】原式=32+3×33×121−2×1×332+3×33×121−2×1×3=3−3=−1
【解析】【分析】求出各特殊角的三角函数值后，进行二次根式化简.
【变式4-1】计算： ∣−8∣+(13)−1−4sin45∘−(2016−2015)0 ．
【答案】解： ∣−8∣+(13)−1−4sin45∘−(2016−2015)0 ，
= 22+3−4×22−1
= 22+3−22−1
=2，
故答案为：2．
【解析】【分析】根据实数的运算顺序，首先计算乘方，开方和乘法，然后从左向右依次计算，求出算式的值即可．
2sin60°+|3−2|+(−1)−3−3−8
【答案】解： 2sin60°+|3−2|+(−1)−3−3−8
2×32+2−3−1+2
=3+2−3−1+2
=3 .
【解析】【分析】根据特殊角的三角函数值、立方根、负指数幂及绝对值的性质进行化简，然后进行加减运算即可.
11．计算：4cs45°+（π+2013）0﹣ 8 +（ 16 ）﹣1．
【答案】解：原式=4× 22 +1﹣2 2 +6
=2 2 +1﹣2 2 +6
=7．
【解析】【分析】根据0指数幂的意义可得（π+2013）0=1，负整数指数幂的意义可得（ 16 ）﹣1 =6，cs45°=22 ，8=22，然后合并同类二次根式即可求解。
3·sin 60°－2·cs 45°＋38－12−1.
【答案】解：原式＝3×32－2×22＋2－2＝32－1＝12
【解析】【分析】考查特殊角的三角函数值。
【变式4-2】先化简，再求值： a−ba+2b÷a2−b2a2+4ab+4b2 ﹣1，其中a=2sin60°﹣tan45°，b=1．
【答案】解：原式= a−ba+2b × (a+2b)2(a+b)(a−b) -1
= a+2ba+b -1
= a+2ba+b−a+ba+b
= ba+b ，
当a═2sin60°﹣tan45°=2× 32 ﹣1= 3 ﹣1，b=1时，
原式= 13−1+1=33 .
【解析】【分析】对待求式的分子、分母进行因式分解，并将除法化为乘法可得 a−ba+2b × (a+2b)2(a+b)(a−b) -1，通过约分即可得到化简结果；先利用特殊角的三角函数值求出a的值，再将a、b的值代入化简结果中计算即可解答本题.
锐角三角函数之间的关系
如图所示，在Rt△ABC中，∠C=90°．
(1)互余关系：，；
(2)平方关系：；
(3)倒数关系：或；
(4)商数关系：．

注意：
锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．
题型5：锐角三角函数之间的关系
5.已知α为一锐角，sinα=45，求csα，tanα．
【答案】解：由sinα=ac=45，设a=4x，c=5x，
则b=c2−a2=3x，
故csα=bc​=35，tanα=ab=43．
【解析】【分析】根据sinα=45，设出关于两边的代数表达式，再根据勾股定理求出第三边长的表达式即可推出csα的值，同理可得tanα的值．
【变式5-1】已知tanα=25，α是锐角，求tan（90°﹣α），sinα，csα的值．
【答案】解：∵如图所示：tanB=tanα=25，
∴设AC=2x，BC=5x，则AB=29x，
∴tan（9O°﹣α）=5x2x=52，
sinα=ACAB=2x29x=22929，
csα=BCAB=5x29x=52929．
【解析】【分析】根据题意表示出AC，BC，AB的长，再利用锐角三角函数定义得出即可．
【变式5-2】在Rt△ABC中，∠C=90°，sinB= 35 ，求csA的值．
【答案】解：在△ABC中，∵∠C=90°，
∴∠A+∠B=90°，
∴csA=sinB= 35 ．
故答案为 35
【解析】【分析】先根据三角形内角和定理得出∠A+∠B=90°，再根据互余两角的三角函数的关系求解．
【变式5-3】已知α+β=90°，且sinα+csβ=3，求锐角α．
【答案】解：由α+β=90°，得sinα=csβ．
sinα+csβ=2sinα=3，
sinα=32，
α=60°．
【解析】【分析】根据一个角的余弦等于它余角的正弦，可得sinα=csβ，根据特殊角三角函数值，可得答案．
题型6：锐角三角函数与圆综合
6.如图，AB是圆O的直径，PB，PC是圆O的两条切线，切点分别为B，C．延长BA，PC相交于点D．
（1）求证：∠CPB=2∠ABC．
（2）设圆O的半径为2，sin ∠PBC= 23 ，求PC的长．
【答案】（1）证明：如图，连接OC
∵PB，PC 是OO的两条切线 ∴PC=PB，∠PCO =∠PBO=90°， ∴∠CPB+ㄥBOC=180° ∵∠DOC+∠BOC=180° ∴∠CPB =∠COD ∵OC=OB， ∴∠OCB=∠OBC ∴∠COD=2∠ABC ∴∠CPB=2∠ABC.
（2）解：∵PC 是圆O的切线，
∴OC⊥CD，
∴∠OCD=90°，
∵圆O 的半径为2，sin∠PDB=23，
∴sin∠CDO=OCOD=23，
∴OD=3，
∴DC= DO2−OC2=32−22=5
设 PC=x，
∴BD2+PB2=PD2
∴(x+ 5 )2=x2+52，
解得 x= 25 ，
∴PC= 25 .
【解析】【分析】（1）根据切线性质可得PC=PB，∠PCO =∠PBO=90°，再结合∠DOC+∠BOC=180°，从而得到∠CPB =∠COD，再通过∠COD=2∠ABC等量代换即可求证∠CPB=2∠ABC成立；
（2）由切线性质及sin ∠PDB= 23，可得出sin∠CDO＝OCOD，求出OD＝3，设PC＝x，利用勾股定理列出关于x的一元二次方程，解得x即可求出PC.
【变式6-1】如图，AB是⊙O的直径，AC切⊙O于点A，连接BC交⊙O于点D，点E是 BD 的中点，连接AE交BC于点F．
（1）求证：AC=CF；
（2）若AB=4，AC=3，求∠BAE的正切值．
【答案】（1）证明：连接AD,BE，
∵CA是⊙O的切线，
∴∠CAB=90°，
∵AB是直径，
∴∠AEB=90°，
∵E是弧BD的中点，
∴∠BAE=∠DAE．
∵AB是⊙O的直径，
∴∠ADB=90°．
∵∠CAD+∠DAB=∠DAB+∠B=90°，
∴∠CAD=∠B．
∵∠CAD+∠DAE =∠B+∠BAE，
∴∠CAF=∠CFA．
∴AC=CF．
（2）解：∵AB=4，AC=3，
∴BC=5．
∵AC=CF=3，
∴BF=2．
∵csB=BDAB=ABBC=45 ，
∴BD= 165 ．
∴AD= 125 ，DF= 65 ．
∴tan∠BAE= tan∠DAE = 12 .
【解析】【分析】（1）连接AD,BE，若要证明AC=CF，则只要证明∠CAE=∠EFB=∠AFC即可；
（2）易证得BF=2，根据cs∠ABC= BDAB = ABBC = 45 ，可求出BD的长，进而得到AD和DF的长，然后根据tan∠BAE=tan∠DAE求得即可．
【变式6-2】如图，AB为⊙O的直径，C为BA延长线上一点，CD与⊙O相切于点D．
（1）求证：△CAD∽△CDB；
（2）若sinC＝13，BD＝6，求⊙O的半径．
【答案】（1）证明：连接OD，
∵CD与⊙O相切于点D，
∴OD⊥CD，
∴∠CDO=90°，
∴∠ADO+∠CDA=90°，
∵AB为⊙O的直径，
∴∠ADB=90°，
∴∠ADO+∠BDO=90°，
∴∠CDA=∠BDO，
∵OB=OD，
∴∠B=∠BDO，
∴∠B=∠CDA，
∵∠C=∠C，
∴△CAD∽△CDB．
（2）解：设圆的半径为r，
∵sinC=ODCO，
即rCO=13，
∴CO=3r，
∴AC=CO−AO=3r−r=2r，
CB=CO+BO=3r+r=4r，
∵△CAD∽△CDB，
∴ADBD=CDBC=ACCD，
∴CD2=AC⋅BC=2r⋅4r=8r2，
∴CD=8r2=22r，
∴AD6=22r4r，
∴AD=32，
∴AB=AD2+BD2=(32)2+62=36，
∴r=12AB=362．
【解析】【分析】（1）连接OD，根据切线的性质可得∠CDO=90°，根据圆周角定理可得∠ADB=90°，由同角的余角相等可得∠CDA=∠BDO，由等腰三角形的性质可得∠B=∠BDO，则∠B=∠CDA，然后根据有两组角对应相等的两个三角形相似进行证明；
（2）设圆的半径为r，根据三角函数的概念可得CO=3r，则AC=CO-AO=2r，CB=CO+BO=4r，根据相似三角形的性质可得CD、AD，利用勾股定理可得AB，据此求解.
题型7：锐角三角函数与平面直角坐标系
7.如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（ ）
A．B．C．D．2
【答案】C
【解析】【解答】解: 设（2，1）点是B，作BC⊥x轴于点C．
则OC=2，BC=1，
则tanα= BCOC = 12 ．
故答案为：C．
【分析】根据勾股定理求出OB，再由tanα=BCOC代入求解.
【变式7-1】点P关于y轴对称的点的坐标是（-sin60°，cs60°），则点P关于x轴的对称点的坐标为（ ）
A．（32，-12）B．（-32，12）
C．（-32，-12）D．（-12，-32）
【答案】A
【解析】【分析】利用关于y轴对称点的性质，关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变．即点P（x，y)关于y轴的对称点P′的坐标是（-x，y)，得出P点坐标，进而得出P关于x轴的对称点的坐标即可．
【解答】∵点P关于y轴对称的点的坐标是（-sin60°，cs60°)，
∴P点坐标为：（32，12)，
则点P关于x轴的对称点的坐标为（32，-12)，
故选：A．
【点评】此题主要考查了关于坐标轴对称点的性质，正确把握横纵坐标关系是解题关键．
【变式7-2】如图，在平面直角坐标系中，已知点A（3，0），点B（0，-4），则tan∠OAB的值为（ ）
A．−43B．34C．43D．−34
【答案】C
【解析】【解答】由点A（3，0)，点B（0，-4)，
∴tan∠OAB=OBOA=43．
故选C．
【分析】根据点A，B的坐标，利用锐角三角函数的定义求解即可得出答案．本题考查了锐角三角函数的定义及坐标与图形的性质，属于基础题，关键是掌握正切值的求法．
【变式7-3】如图，已知A点坐标为（5，0），直线y=x+b（b＞0）与y轴交于点B，连接AB，∠α=75°，则b的值为（ ）
A．3B．533C．4D．534
【答案】B
【解析】【分析】设直线y=x+b与x轴交于点C，则点B的坐标是（0，b)，点C的坐标是（-b，0)，所以OB=OC，∠ACB=45°，因为∠α=75°，所以∠BAC=30°，因为OA=5，根据正切函数tan∠BAC=OBOA=33，所以OB=533，即b=533，故选B.
题型8：锐角三角函数与一元二次方程综合
8.在Rt△ABC中,∠C=90°,sin A的值是方程2x2-5x+2=0的一个根,求sin A的值.
【答案】解:2x2-5x+2=0得:x1= 12 ,x2=2,因为∠A为锐角,所以0【解析】【分析】可运用因式分解法解2x2-5x+2=0，得出两个解，但0【变式8-1】已知α为锐角，且tanα是方程x2+2x﹣3=0的一个根，求2sin2α+cs2α﹣3tan（α+15°）的值．
【答案】解：解方程x2+2x﹣3=0得：x1=1，x2=﹣3，∵tanα＞0，∴tanα=1，∴α=45°，∴2sin2α+cs2α﹣3tan（α+15°）=2sin245°+cs245°﹣3tan60°=2•（22）2+（22）2﹣3•3=1+12﹣3=−32．
【解析】【分析】先求出tanα的值，求出α的度数，然后将特殊角的三角函数值代入求解即可．
【变式8-2】已知α为锐角且csα是方程2x2﹣7x+3=0的一个根，求 1−2sinαcsα 的值．
【答案】解：∵csα是方程2x2﹣7x+3=0的一个根，
∴由求根公式有，csα= −(−7)±(−7)2−4×2×32×2 ，
∴csα= 12 （csα=3不符合题意，舍去），
∵sin2α+cs2α=1，
∴sin2α=1﹣（ 12 ）2= 34 ，
∴sinα= 32 ，
∴1−2sinαcsα = sin2α+cs2α−2sinαcsα = (sinα−csα)2 =sinα﹣csα= 3−12
【解析】【分析】首先求出已知一元二次方程的根，然后根据csα是方程的一个根可求出csα的值或α的度数，则代数式的值可求。
题型9：利用三角函数值确定三角形类型
9.△ABC中，∠A、∠B均为锐角，且|2sinA﹣|+（1﹣tanB）2＝0，请判断△ABC的形状．
【分析】根据非负数的性质列出关系式，根据特殊角的三角函数值求出∠A、∠B的度数，根据三角形内角和定理求出∠C的度数，判断即可．
【解答】解：由题意得，2sinA﹣＝0，1﹣tanB＝0，
即2sinA＝，tanB＝1，
解得∠A＝60°，∠B＝45°，
则∠C＝180°﹣60°﹣45°＝75°，
故△ABC是锐角三角形．
【点评】本题考查的是特殊角的三角函数值和非负数的性质，熟记特殊角的三角函数值是解题的关键．
【变式9-1】在△ABC中，csA＝，tanC＝，试判断△ABC的形状．
【分析】根据特殊角的三角函数值求出∠A、∠B的度数，根据三角形内角和定理求出∠B的度数，判断即可．
【解答】解：∵csA＝，
∴∠A＝45°，
∵tanC＝，
∴∠C＝30°，
∴∠B＝180°﹣30°﹣45°＝105°，
∴△ABC是钝角三角形．
【点评】本题考查的是特殊角的三角函数值，熟记特殊角的三角函数值、掌握三角形内角和定理是解题的关键．
【变式9-2】在△ABC中，若（2csA﹣1）2+|﹣tanB|＝0，试判断△ABC的形状．
【分析】根据非负数的和为零，可得每个非负数同时为零，根据特殊角三角函数值，可得答案．
【解答】解：由（2csA﹣1）2+|﹣tanB|＝0，得
2csA﹣1＝0，﹣tanB＝0，
解得csA＝，tanB＝，
A＝60°，B＝60°，
△ABC是等边三角形．
【点评】本题考查了特殊角三角函数值，利用非负数的和为零得出每个非负数同时为零是解题关键，要熟记特殊角三角函数值．
题型10：锐角三角函数阅读理解
10.如图，根据图中数据完成填空，再按要求答题：
sin2A1+sin2B1＝ ；
sin2A2+sin2B2＝ ；
sin2A3+sin2B3＝ ．
（1）观察上述等式，猜想：在Rt△ABC中，∠C＝90°，都有sin2A+sin2B＝ ．
（2）如图4，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别是a，b，c，利用三角函数的定义和勾股定理，证明你的猜想．
【分析】（1）根据三角函数的定义和所给信息可完成前面三个空，根据前面的三个等式的值，猜想出在Rt△ABC中，∠C＝90°，sin2A+sin2B的值；
（2）在Rt△ABC中，∠C＝90°，利用锐角三角函数的定义得出sinA＝，sinB＝，则sin2A+sin2B＝，再根据勾股定理得到a2+b2＝c2，从而证明结论．
【解答】解：（1）由图可知：sin2A1+sin2B1＝（）2+（）2＝1，
sin2A2+sin2B2＝（）2+（）2＝1，
sin2A3+sin2B3＝（）2+（）2＝1，
观察上述等式，可猜想：sin2A+sin2B＝1．
（2）如图，在Rt△ABC中，∠C＝90°．
∵sinA＝，sinB＝，
∴sin2A+sin2B＝．
∵∠C＝90°，
∴a2+b2＝c2，
∴sin2A+sin2B＝1．
【点评】本题考查了三角函数，掌握用勾股定理证明三角函数之间的关系是解答本题的关键．
【变式10-1】如图，定义：在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα＝＝，根据上述角的余切定义，解下列问题：
（1）ctan30°＝ ；
（2）如图，已知tanA＝，其中∠A为锐角，试求ctanA的值．
【分析】（1）根据直角三角形的性质用AC表示出AB及AC的值，再根据锐角三角函数的定义进行解答即可；
（2）由于tanA＝，所以可设BC＝3x，AC＝4x，则AB＝5x，再根据锐角三角函数的定义进行解答即可．
【解答】解：（1）∵Rt△ABC中，α＝30°，
∴BC＝AB，
∴AC＝＝＝AB，
∴ctan30°＝＝．
故答案为：；
（2）∵tanA＝，
∴设BC＝3x，AC＝4x，
∴ctanA＝＝＝．
【点评】本题考查的是锐角三角函数的定义及直角三角形的性质，熟知锐角三角函数的定义是解答此题的关键．
【变式10-2】在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，∠C＝90°．若定义ctA＝，则称它为锐角A的余切，根据这个定义解答下列问题：
（1）ct30°＝ ；
（2）已知tanA＝，其中∠A为锐角，试求ctA的值；
（3）求证：tanA＝ct（90°﹣∠A）．
【分析】（1）在Rt△ABC中，∠C＝90°，设∠A＝30°，根据直角三角形的性质用BC表示出AC的值，再根据余切的定义进行解答即可；
（2）在Rt△ABC中，∠C＝90°，设BC＝3k，则AC＝4k，再根据余切的定义进行解答即可；
（3）在Rt△ABC中，∠C＝90°，根据三角形内角和定理得出∠A+∠B＝90°，∠B＝90°﹣∠A，再根据三角函数的定义得出tanA＝，ctB＝，进而得到tanA＝ct（90°﹣∠A）．
【解答】解：（1）如图，在Rt△ABC中，∠C＝90°，
设∠A＝30°，则AB＝2BC，AC＝BC，
所以ct30°＝＝＝．
故答案为；
（2）在Rt△ABC中，∠C＝90°，
∵tanA＝＝，
∴可设BC＝3k，则AC＝4k，
∴ctA＝＝＝；
（3）在Rt△ABC中，∠C＝90°，
则∠A+∠B＝90°，
即∠B＝90°﹣∠A，
∵tanA＝，ctB＝，
∴tanA＝ctB，
即tanA＝ct（90°﹣∠A）．
【点评】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．也考查了直角三角形的性质及学生的阅读理解能力．