苏科版九年级下册7.5 解直角三角形习题

这是一份苏科版九年级下册7.5 解直角三角形习题，文件包含专项训练解直角三角形及应用40题原卷版docx、专项训练解直角三角形及应用40题解析版docx等2份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。
一、解答题
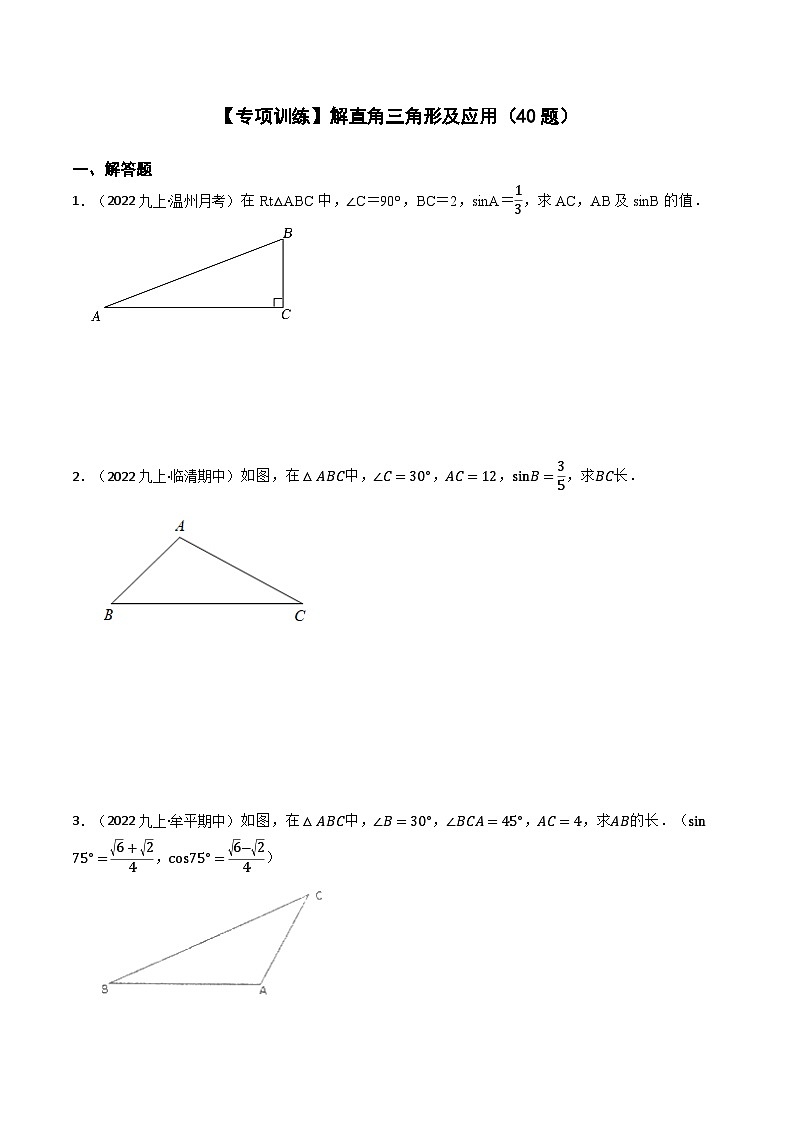
1．（2022九上·温州月考）在Rt△ABC中，∠C＝90°，BC＝2，sinA＝13，求AC，AB及sinB的值．
【答案】解：在Rt△ABC中，∠C＝90°，BC＝2，sinA＝13，
∴sinA＝BCAB＝13，即2AB＝13，
∴AB＝6，
∴AC＝AB2−BC2=62−22=42，
∴sinB＝ACAB=426=223.
【解析】【分析】先根据正弦函数的定义求出AB，再利用勾股定理求出AC，最后根据正弦函数的定义，即可求出sinB的值．
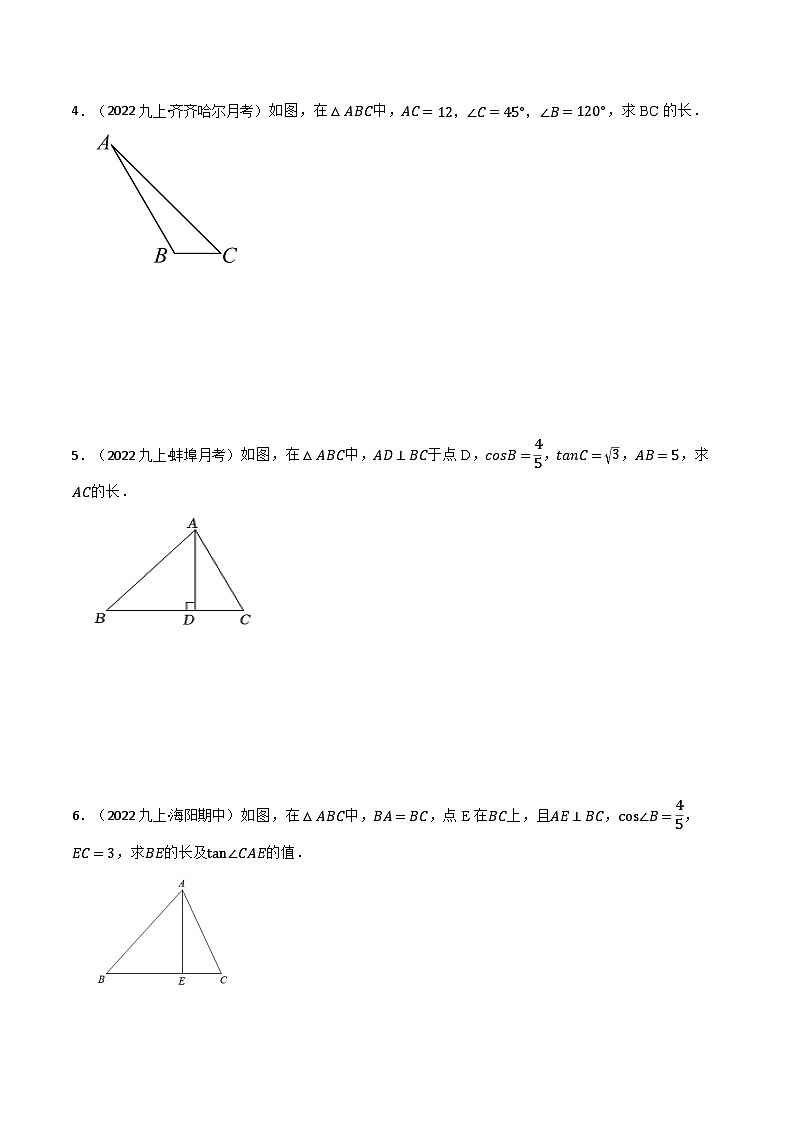
2．（2022九上·临清期中）如图，在△ABC中，∠C=30°，AC=12，sinB=35，求BC长．
【答案】解：过点A作AD⊥BC，垂足为D
在Rt△ADC中，AC=12，∠C=30°
∴AD=12AC=6，CD=3AD=63
在Rt△ABD中，sinB=35
∴AB=10
∴BD=8
∴BC=BD+CD=8+63
∴BC长为8+63
【解析】【分析】过点A作AD⊥BC，垂足为D，先利用含30°角的直角三角形的性质求出AD=12AC=6，CD=3AD=63，再解直角三角形求出AB和BD，最后利用线段的和差求出BC的长即可。
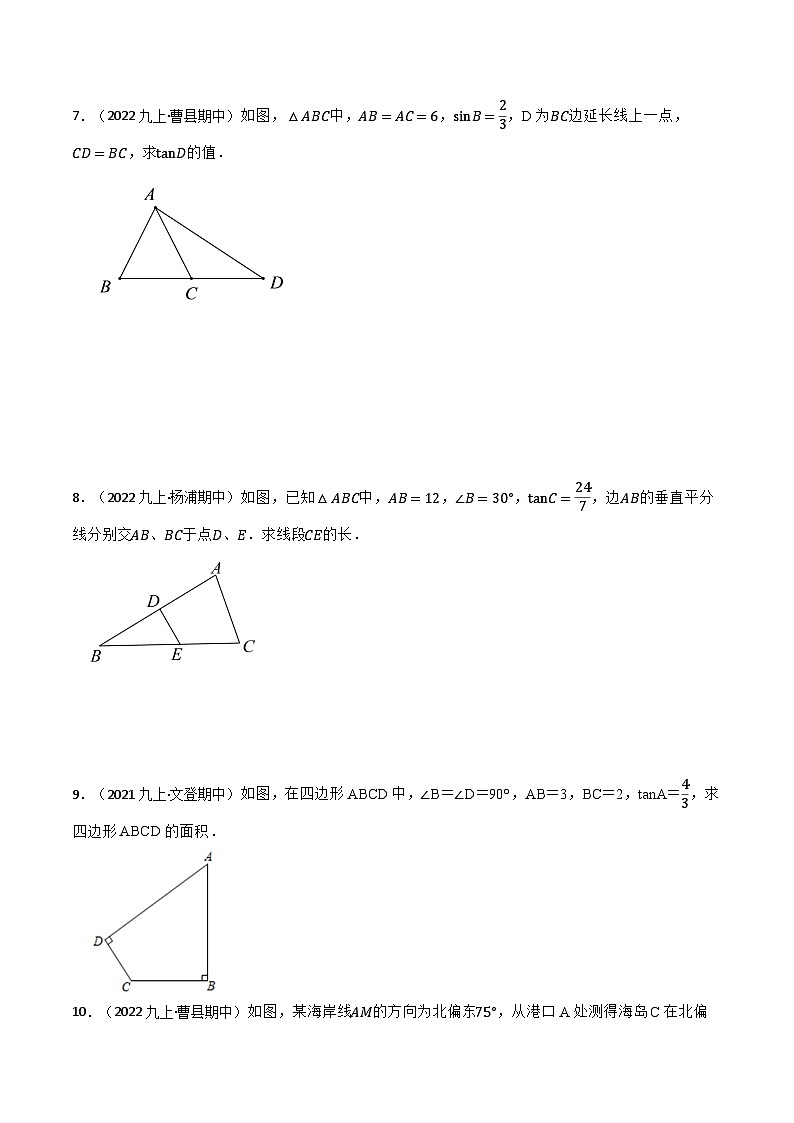
3．（2022九上·牟平期中）如图，在△ABC中，∠B=30°，∠BCA=45°，AC=4，求AB的长．（sin75°=6+24，cs75°=6−24）
【答案】解：过C作CD⊥AB，交BA的延长线于点D．
∵∠B=30°，∠BCA=45°，
∴∠CAD=∠B+∠BCA=75°，
在Rt△ACD中，AC=4，∠CAD=75°，
∴AD=AC⋅cs∠CAD=4cs75°=6−2
CD=AC⋅sin∠CAD=4sin75°=6+2
在Rt△BCD中，∠B=30°，
∴BD=CDtanB=6+2tan30°=32+6
∴AB=BD−AD=32+6−6+2=42．
【解析】【分析】
过C作CD⊥AB，交BA的延长线于点D ， 根据三角形外角的性质求出∠CAD.在Rt△ACD中，求出AD， CD，在Rt△BCD中，求出BD，再利用AB= BD- AD即可求解。
4．（2022九上·齐齐哈尔月考）如图，在△ABC中，AC=12，∠C=45°，∠B=120°，求BC的长．
【答案】解：过点A作AD⊥BC，交BC的延长线于点D，则∠ADC=90°，
在Rt△ADC中，∠C=45°，
∴AD=DC，
根据勾股定理可得：AD2+DC2=AC2，
即 2AD2=AC2=122，
解得AD=DC=62，
∵∠ABC=120° ，
∴∠ABD=60°，
在Rt△ABD中，
设BD=x，则AB=2x，
根据勾股定理可得：AD2+DB2=AB2，
即(62)2+x2=(2x)2，
解得x=26，
即BD=26，
∴BC=DC−DB=62−26．
【解析】【分析】过点A作AD⊥BC，交BC的延长线于点D，则∠ADC=90°，设BD=x，则AB=2x，根据勾股定理可得(62)2+x2=(2x)2，求出x=26，再利用线段的和差求出BC=DC−DB=62−26即可。
5．（2022九上·蚌埠月考）如图，在△ABC中，AD⊥BC于点D，csB=45，tanC=3，AB=5，求AC的长．
【答案】解：∵AD⊥BC，
∴∠ADB=∠ADC=90°，
∵csB=45，AB=5，
∴BD=AB·csB=5×45=4，
∴AD=AB2−BD2=52−42=3，
∵tanC=3，
∴CD=ADtanC=33=3
∴AC=AD2+CD2=32+(3)2=23
【解析】【分析】根据csB=45，AB=5，求出BD=AB·csB=5×45=4，再利用tanC=3求出CD=ADtanC=33=3，最后利用勾股定理求出AC的长即可。
6．（2022九上·海阳期中）如图，在△ABC中，BA=BC，点E在BC上，且AE⊥BC，cs∠B=45，EC=3，求BE的长及tan∠CAE的值．
【答案】解：∵AE⊥BC，cs∠B=45，
∴BEAB=45，设BE=4x，则AB=5x，
∵BA=BC，则BC=5x，
∵EC=3，EC=BC−BE，
∴5x−4x=3，即x=3，
∴BE=4x=12，BA=BC=5x=15，
∴AE=AB2−AE2=152−122=9，
∴tan∠CAE=CEAE=39=13.
【解析】【分析】由题意得出BEAB=45，设BE=4x，则AB=5x，根据EC=3，EC=BC−BE，列出方程得出x的值，利用勾股定理得出AE的值，再利用正切性质即可得解。
7．（2022九上·曹县期中）如图，△ABC中，AB=AC=6，sinB=23，D为BC边延长线上一点，CD=BC，求tanD的值．
【答案】解：如图，过点A作AE⊥BD于点E．
∴sinB=AEAB=23．
∵AB=AC=6，
∴AE=4，
∴BE=AB2−AE2=25．
∵AE⊥BD，AB=AC=6，
∴CE=BE=25，
∴CD=BC=BE+CE=45，
∴DE=CD+CE=65，
∴tanD=AEDE=465=2515
【解析】【分析】过点A作AE⊥BD于点E，根据勾股定理得出BE的值，由AE⊥BD，AB=AC=6，得出CE的值，从而得出CD、DE的值，由此得出答案。
8．（2022九上·杨浦期中）如图，已知△ABC中，AB=12，∠B=30°，tanC=247，边AB的垂直平分线分别交AB、BC于点D、E．求线段CE的长．
【答案】解：过A作AH⊥BC，垂足为点H，如图所示：
在Rt△ABH中，∠B=30°，AB=12，
∴AH=6，BH=63，
在Rt△ACH中，tanC=AHCH=247，
∴CH=74，
∴BC=BH+CH=63+74，
∵DE垂直平分AB，
∴BD=12AB=6，DE⊥AB，
在Rt△BDE中，csB=BDBE=32，
∴BE=43，
∴CE=BC−BE=63+74−43=23+74．
【解析】【分析】过A作AH⊥BC，垂足为点H，在Rt△ABH中，∠B=30°，AB=12，得出AH=6，BH=63，在Rt△ACH中，tanC=AHCH=247，得出CH的值，代入得出BC，在Rt△BDE中，csB=BDBE=32，得出BE的值，代入求解即可。
9．（2021九上·文登期中）如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3，BC＝2，tanA＝43，求四边形ABCD的面积．
【答案】解：如图，延长AD、BC相交于点E，
∵∠B=90°，
∴tanA=BEAB=43，
∴BE=43AB=4，
∴CE=BE-BC=2， AE=AB2+BE2=5，
∴sinE=ABAE=35，
又∵∠CDE=∠CDA=90°，
∴在Rt△CDE中，sinE=CDCE，
∴CD=CE⋅sinE=2×35=65，
∴DE=CE2−CE2=85，
∴S四边形ABCD=S△ABE−S△EDC
=12AB⋅BE−12CD⋅BE
=12×3×4−12×65×85
=12625．
【解析】【分析】延长AD、BC相交于点E，先求出CD=CE⋅sinE=2×35=65，利用勾股定理求出DE的长，再利用割补法可得S四边形ABCD=S△ABE−S△EDC，最后将数据代入计算即可。
10．（2022九上·曹县期中）如图，某海岸线AM的方向为北偏东75°，从港口A处测得海岛C在北偏东45°方向，从港口B处测得海岛C在北偏东30°方向，已知港口A与海岛C的距离为36海里，求港口B与海岛C的距离．
【答案】解：过点C作CD⊥AM，垂足为D，
由题意得，∠CAD=75°−45°=30°，∠CBD=75°−30°=45°，
∵港口A与海岛C的距离为36海里，即AC=36(海里)，
∴CD=12AC=18(海里)，
∵∠CBD=75°−30°=45°，
∴CD=BD=18(海里)，
∴BC=182+182=182(海里)，
答：港口B与海岛C的距离为182海里．
【解析】【分析】过点C作CD⊥AM，垂足为D，构造直角三角形得出∠CAD=75°−45°=30°，∠CBD=75°−30°=45°，由港口A与海岛C的距离为36海里，即AC=36(海里)，得出CD的值，利用勾股定理即可得解。
11．（2022九上·即墨期末）自开展“全民健身运动”以来，喜欢户外步行健身的人越来越多，为方便群众步行健身，某地政府决定对一段如图（1）所示的坡路进行改造．如图（2）所示，改造前的斜坡的高度AE=100米，坡角∠ABE=30°；将斜坡AB的高度AE降低20米后，斜坡AB改造为斜坡CD，其坡度为1：4，改造后的斜坡多占多长一段地面？（结果保留根号）
【答案】解：∵∠AEB=90°，AE=100米，∠ABE=30°，
∴AB=AEsin30°=10012=200米，
∴BE=AB⋅cs30°=200×32=1003米，
∵AC=20米，
∴CE=100−20=80米，
∵斜坡CD的坡度为1∶4，即tan∠CDE=14，
∴CEED=14，即80ED=14，
∴DE=320米，
∴BD=DE−BE=320−1003（米），
答：改造后的斜坡多占的地面为(320−1003)米．
【解析】【分析】先利用解直角三角形的方法求出BE=AB⋅cs30°=200×32=1003，DE=320，再利用线段的和差求出BD=DE−BE=320−1003即可。
12．（2022九上·胶州期末）如图是旗杆AB竖直放置在矩形平台EFMC上的示意图，在某一时刻旗杆AB形成的影子的顶端恰好落在斜坡CD的D处，点F，M，D在一条直线上，现测得BC=10m，CD=8m，∠CDF=30°，∠ADF=45°，求旗杆AB的高度．
【答案】解：如图：延长AB交FM于点 N，则∠BNM=90°
又∵∠CMN=∠BCM=90°
∴四边形BNMC为矩形
∴NM=BC=10m，BN=CM
在Rt△CMD中，
∵sin∠CDM=CMCD，cs∠CDM=MDCD
∴CM=CD×sin∠CDM=8×12=4m
DM=DC×cs∠CDM=8×32=43m
∴ND=NM+MD=10+43m
在 Rt△ADN 中，
∵tan∠ADN=ANDN
∴AN=DN×tan∠ADN=10+43m
∴AB=AN−BN=10+43−4=6+43m
答：旗杆AB的高度为(6+43)m．
【解析】【分析】延长AB交FM于点 N，先利用解直角三角形的方法求出AN=DN×tan∠ADN=10+43，再利用线段的和差求出AB=AN−BN=10+43−4=6+43即可。
13．（2022九上·栖霞期中）某型号飞机的机翼形状如图所示，根据图中数据计算AC，BD和AB的长度（结果保留小数点后两位）．
【答案】解：如图，过点D作DF⊥AB，交AB的延长线于点F，过点C作CE⊥AB交AB的延长线于点E，
∴四边形CDFE是矩形，
∴EF=CD=3.40m，CE=DF=5.00m，
在Rt△ACE中，cs∠ECA=CECA，
∴CA=5cs45°=52≈7.07m，
在Rt△BDF中，cs∠BDF=DFDB，
∴DB=5.00cs30°=1033≈5.77m，
∵∠FDB=30°，
∴BF=12DB=12×5.77=2.89m，
∵AB+AE=EF+BF，
∴AB=EF+BF−AE=3.4+2.89−5=1.29m，
∴AC≈7.07m，BD≈5.77m， AB≈1.29m．
【解析】【分析】在Rt∆CEA中，利用45°的余弦可计算出CA，在Rt∆BDF中利用30°的余弦可计算出DB进而求出 BF的值，然后利用AB+AE=EF+BF计算AB的长．
14．（2022九上·柯城月考）一个长方体木箱沿斜面下滑，当木箱滑至如图所示位置时，AB=2m.已知木箱高度BE=1m，斜面坡角∠BAC为30°，求木箱端点E距地面AC的高度.
【答案】解：过E作EH⊥AC交AC于H，交AB于G，如图，
由题意可得，
∠BAC+∠AGH=90°，∠BEG+∠BGE=90°，∠AGH=∠BGE，且∠BAC为30°，
∴∠BAC=∠BEG=30°，
∵cs∠BEG=cs30°=BEEG ，tan∠BEG=tan30°=BGBE ，BE=1m，
∴GE=BEcs30°=233 ，BG=BE×tan30°=33 ，
∵AB=2m，
∴AG=AB−BG=2−33
∵cs∠BAC=cs30°=GHGA，
∴GH=AG×cs30°=(2−33)×32=3−12，
EH=EG+GH=233+3−12=533−12 .
【解析】【分析】 过E作EH⊥AC交AC于H，交AB于G， 根据等角的余角相等得∠BAC=∠BEG=30°，根据锐角三角函数的定义及特殊锐角三角函数值可得GE、BG的长，根据线段的和差得AG的长，最后再根据正切函数的定义及特殊锐角三角函数值算出GH的长，从而就不难求出EH的长了.
15．（2022九上·义乌月考）如图，小明站在斜坡AB上的点A处，看到坡下一棵大树顶端的影子刚好落在山脚下的B处（点A与大树及其影子在同一平面内），此时太阳光与地面成60°角，在点A处测得大树顶端的俯角为15°.已知山坡AB的坡比为3：1，AB为10米，请帮助小明计算这棵大树的高度.（结果精确到0.1米，参考数据：3≈1.732）
【答案】解：过D作DM⊥AB于M，过A作AF⊥BC于F，
∵山坡AB的坡比为3：1，
∴tan∠ABF=AFBF=3，
∴∠ABF=60°，
∴∠ABD=180°-∠ABF-∠DBC=60°，
∴在Rt△MBD中，
tan∠MBD=MDBM=3，
设MB=x，则MD=3x，
∵AE∥CB，
∴∠EAB=∠ABF=60°，
∴∠DAM=∠EAM-∠EAD=45°，
在Rt△AMD中，
tan∠MAD=MDMA=1，
∴AM=MD=3x，
∴3x+x=10，
∴x=53-5，
在Rt△MBD中，cs∠MBD=MBBD=12，
∴BD=2x=103-10，
∵sin∠DBC=DCBD=32，
∴DC=15-53≈6.3(米)，
答：这棵大树的高度约为6.3米.
【解析】【分析】 过D作DM⊥AB于M，过A作AF⊥BC于F， 根据坡比的定义及特殊锐角三角函数值可得∠ABF=60°，根据平角的定义得∠ABD=60°，在Rt△MBD及 Rt△AMD中，根据正切函数的定义及特殊锐角三角函数值可设 MB=x，则MD=3x ， AM=MD=3x， 进而根据AM+BM=AB=10建立方程，求解得出x的值， 在Rt△MBD中 ，根据余弦函数的定义可得 BD=2x=103-10， 最后根据 sin∠DBC=DCBD=32， 即可算出DC的长得出答案.
16．（2022九上·闵行期中）如图，在电线杆上的C处引拉线CE和CF固定电线杆．在离电线杆6米的B处安置测角仪（点B、E、D在同一直线上），在点A处测得电线杆上C处的仰角为30°．已知测角仪的高AB为3米，拉线CE的长为6米，求测角仪底端（点B）与拉线固定点（E）之间的距离．
【答案】解：如图：
过A作AM垂直于CD，垂足为点M，
则AM=BD=6米，MD=AB=3米，∠AMC=90°，
∵∠CAM=30°，
∴CM=12AC，
∵AC2−CM2=AM2，
∴3CM2=36，
∴CM=23（米），
∴CD=33（米），
∵CE=6米，
利用勾股定理得DE=CE2−CD2=62−（33）2=9=3（米），
∴BE=6−3=3（米）．
答：测角仪底端（点B）与拉线固定点（E）之间的距离是3米．
【解析】【分析】过A作AM垂直于CD，垂足为点M，利用含30°角的直角三角形的性质可得CM=12AC，再结合AC2−CM2=AM2，求出CM=23，利用勾股定理求出DE的长，再利用线段的和差求出BE的长即可。
17．（2022·淮安）如图，湖边A、B两点由两段笔直的观景栈道AC和CB相连.为了计算A、B两点之间的距离，经测量得：∠BAC=37°，∠ABC=58°，AC=80米，求A、B两点之间的距离.（参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75，sin58°≈0.85，cs58°≈0.53，tan58°≈1.60）
【答案】解：如图，过点C作CD⊥AB，垂足为点D，
在Rt△ACD中，
∵∠DAC=37°，AC=80米，
∴sin∠DAC=CDAC，cs∠DAC=ADAC，
∴CD=AC⋅sin37°≈80×0.60=48（米），
AD=AC⋅cs37°≈80×0.80=64（米），
在Rt△BCD中，
∵∠CBD=58°，CD=48米，
∴tan∠CBD=CDBD，
∴BD=CDtan58°≈481.60=30（米），
∴AB=AD+BD=64+30=94（米）.
答：A、B两点之间的距离约为94米.
【解析】【分析】 过C作CD⊥AB于D，在Rt△ACD中，用三角函数定义得CD=AC×sin37°，AD=AC×cs37°，在Rt△BCD中，用三角函数定义得 BD=CDtan58°，代入求值可分别算出CD、AD，BD的长，最后根据AB=AD+BD算出答案.
18．如图，甲乙两艘渔船从港口A同时出发前往某海域捕鱼，甲船以16海里/时的速度向南偏东50°航行，乙船向北偏东40°航行，3小时后，甲船到达B岛，乙船到达C岛，若C、B两岛相距60海里，问乙船的航速是多少？
【答案】解：根据题意，得 ∠CAB=180°−40°−50°=90° ，
∵AC=16×3=48( 海里 ) ， BC=60 海里，
∴ 在直角三角形 ABC 中，根据勾股定理得： AB=602−482=36( 海里 ) .
则乙船的速度是 36÷3=12 海里 / 时.
【解析】【分析】根据题意得 ∠CAB=90°，AC=16×3=48海里，BC=60海里，利用勾股定理求出AB，然后除以时间就可求出乙船的速度.
19．（2022九上·乳山期中）一次数学活动课上，老师带领学生去测一条东西流向的河宽，如图所示，小明在河北岸点A处观测到河对岸有一点C在A的南偏西60°的方向上，沿河岸向西前行20m到达B处，又测得C在B的南偏西45°的方向上，请你根据以上数据，帮助小明计算出这条河的宽度．（结果保留根号）
【答案】解：过点C作CD⊥AB于D．
设CD=xm．
∵在Rt△BCD 中，∠CBD=45°，
∴BD=CD=xm．
在Rt△ACD中，∠ACD=60°，
AD=AB+BD=(20+x)m，CD=xm，
∴tan∠ACD=ADCD．
即20+xx=3．
解得x=103+10．
∴这条河的宽度为(103+10)m．
【解析】【分析】过点C作CD⊥AB于D，设CD=xm，则AD=AB+BD=(20+x)m，CD=xm，再根据tan∠ACD=ADCD，可得20+xx=3，求出x的值即可。
20．（2022九上·莱西期中）某学校升气球庆祝党的二十大胜利召开．如图，一气球到达离地面高度为12米的A处时，仪器显示正前方一高楼顶部B的仰角是37°，底部C的俯角是60°．气球要飞到楼顶，应至少再上升多少米？（结果精确到0.1米）（参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75，3≈1.73）
【答案】解：过A作AD⊥BC，垂足为点D，过A作AE⊥EC，垂足为点E，
根据题意，楼BC⊥EC，
∴四边形AECD是矩形，
∴CD=AE，△ADC和△ADB都是直角三角形，
∵气球到达离地面高度为12米的A处时，仪器显示正前方高楼顶部B的仰角是37°，底部C的俯角是60°，
∴CD=AE=12，∠CAD=60°，∠BAD=37°，
在Rt△ADC中，
∵CD=12，∠CAD=60°．
∴AD=CDtan60°=123≈6.94，
在Rt△ADB中，
∵AD≈6.94，∠BAD=37°．
∴BD=AD×tan37°≈6.94×0.75=5.205≈5.2（米）．
答：气球应至少再上升5.2米．
【解析】【分析】过A作AD⊥BC，垂足为点D，过A作AE⊥EC，垂足为点E，根据解直角三角形的方法可得AD=CDtan60°=123≈6.94，再求出BD=AD×tan37°≈6.94×0.75=5.205≈5.2即可。
21．（2022八上·宝鸡月考）如图，某港口O位于南北延伸的海岸线上，东面是大海．远洋号、长峰号两艘轮船同时离开港O，“远洋”号沿着北偏东60°方向航行，“长峰”号沿着南偏东30°方向匀速航行，“远洋”号每小时航行12海里，“长峰”号每小时航行16海里，它们离开港口1小时后，分别到达A，B两个位置，求1小时后远洋号、长峰号两艘轮船相距多少海里．
【答案】解：∵“远洋”号沿着北偏东60°方向航行，“长峰”号沿着南偏东30°方向匀速航行，
∴∠AOB=180°−60°−30°=90°，
∵“远洋”号每小时航行12海里，“长峰”号每小时航行16海里，
∴OA=12海里，OB=16海里，
∴AB=OA2+OB2=122+162=20（海里），
答：1小时后远洋号、长峰号两艘轮船相距20海里．
【解析】【分析】由题意可得∠AOB=90°，OA=12海里，OB=16海里，然后利用勾股定理计算即可.
22．（2022·西藏）某班同学在一次综合实践课上，测量校园内一棵树的高度．如图，测量仪在A处测得树顶D的仰角为45°，C处测得树顶D的仰角为37°（点A，B，C在一条水平直线上），已知测量仪高度AE＝CF＝1.6米，AC＝28米，求树BD的高度（结果保留小数点后一位．参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75）．
【答案】解：连接EF，交BD于点M，
则EF⊥BD，AE＝BM＝CF＝1.6米，
在Rt△DEM中，∠DEM＝45°，
∴EM＝DM，
设DM＝x米，则EM＝AB＝x米，FM＝BC＝AC﹣AB＝（28﹣x）米，
在Rt△DFM中，tan37°＝DMFM，
即x28−x≈0.75，
解得x＝12，
经检验，x＝12是原方程的根，
即DM＝12米，
∴DB＝12+1.6＝13.6（米），
答：树BD的高度为13.6米．
【解析】【分析】连接EF，交BD于点M，则EF⊥BD，AE＝BM＝CF＝1.6米，EM＝DM，设DM＝x米，则EM＝AB＝x米，FM＝BC＝(28-x)米，根据正切三角函数的概念可得x的值，然后根据DB=DM+BM进行计算.
23．（2021九上·牟平期中）某区域平面示意图如图所示，点D在河的右侧，人民路AB与桥BC垂直．某校数学小组进行研学活动时，在C处测得点D位于西北方向，又在A处测得点D位于南偏东65°方向，另测得BC＝628m，AB＝400m，求出点D到AB的距离，（结果保留整数，参考数据sin65°≈0.91，cs65°≈0.42，tan65°≈2.14）
【答案】解：如图，过点D作DE⊥AB于点E，过D作DF⊥BC于点F，则四边形EBFD是矩形，
设DE＝x m，
在Rt△ADE中，∠AED＝90°，
∵tan∠DAE＝DEAE，
∴AE＝DEtan∠DAE≈x2.14，
∴BE＝400－x2.14，
又BF＝DE＝x m，
∴CF＝(628−x)m，
在Rt△CDF中，∠DFC＝90°，∠DCF＝45°，
∴DF＝CF＝(628−x)m，
又BE＝DF，即400－x2.14＝628﹣x，
解得x＝428，
答：点D到AB的距离约是428m．
【解析】【分析】利用锐角三角函数计算求解即可。
24．（2021九上·福山期中）如图，甲楼高40m，在甲楼楼顶D处、楼底A处分别测得乙楼楼顶B处的仰角为30°，60°．DE⊥BC，垂足为点E．求乙楼的高度BC．
【答案】解：设BE=x．
在Rt△BED中，
∵∠BDE=30°，
∴∠DBE=60°．
∴DE=BEtan60°=3x．
在Rt△ACB中，
∵∠BAC=60°，
∴∠ABC=30°．
∴AC=BCtan30°=33(40+x)．
∵DE=AC，
∴3x=33(40+x)，
∴x=20．
∴BC=BE+CE=20+40=60(m)．
答：乙楼的高度BC为60米．
【解析】【分析】利用锐角三角函数计算求解即可。
25．（2022七下·新城期末）如图，某天数学活动课上，王婷想利用所学知识测量学校旗杆AB的高度，她在距离旗杆底端B处3米高的点C处做好标记（即BC=3米），用测角仪在地面上的点E处测得点C的仰角∠1的度数，然后沿EB到达点D处，测得旗杆顶端A的仰角∠2的度数，发现∠1+∠2=90°，经测量BE=10米，BD=3米，已知点B、D、E在同一水平直线上，AB⊥ED，求旗杆AB的高度．
【答案】解：∵AB⊥ED，
∴∠CBE=∠ABD=90°，
∴∠2+∠A=90°，
∵∠1+∠2=90°，
∴∠1=∠A，
∵BC=BD=3，
∴△EBC≌△ABD，
∴BE=AB，
∵BE=10，
∴AB=10，
答：旗杆的高度AB为10米．
【解析】【分析】 根据垂直的概念得∠CBE=∠ABD=90°，则∠2+∠A=90°，结合∠1+∠2=90°，得∠1=∠A，结合BC=BD可证明△EBC≌△ABD，得到BE=AB，据此解答.
26．（2022·菏泽）荷泽某超市计划更换安全性更高的手扶电梯，如图，把电梯坡面的坡角由原来的37°减至30°，已知原电梯坡面AB的长为8米，更换后的电梯坡面为AD，点B延伸至点D，求BD的长．（结果精确到0.1米．参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0，75，3≈1.73）
【答案】解：在Rt△ABC中，AB=8米，∠ABC=37°，
则AC=AB•sin∠ABC≈8×0.60=4.8（米），
BC=AB•cs∠ABC≈8×0.80=6.40（米），
在Rt△ADC中，∠ADC=30°，
则CD=ACtan∠ADC=4.8tan30°=4.833≈8.30（米），
∴BD=CD-BC=8.30-6.40≈1.9（米），
答：BD的长约为1.9米．
【解析】【分析】利用锐角三角函数计算求解即可。
27．（2022八下·交口期末）某校秉承“学会生活，学会学习，学会做人”的办学理念，将本校的办学理念做成宣传牌（AB），放置在教室的黑板上面（如图所示）．在三月雷锋活动中小明搬来一架梯子（AE＝5米）靠在宣传牌（AB）A处，底端落在地板E处，然后移动的梯子使顶端落在宣传牌（AB）的B处，而底端E向外移到了1米到C处（CE＝1米）．测量得BM＝4米．求宣传牌（AB）的高度（结果用根号表示）．
【答案】解：由题意可得：AE＝BC＝5米，BM＝4米，EC＝1米，
在Rt△MBC中，MC=BC2−BM2=52−42=3（米），
则EM＝3﹣1＝2（米），
在Rt△AEM中，AM=AE2−EM2=52−22=21（米），
则AB=AM−BM=(21−4)米，
即宣传牌（AB）的高度为(21−4)米．
【解析】【分析】 由题意可得：AE＝BC＝5米，BM＝4米，EC＝1米，在Rt△MBC中，根据勾股定理可得MC=BC2−BM2=3（米），则EM＝3﹣1＝2（米），在Rt△AEM中，根据勾股定理可得AM=AE2−EM2=21（米），则AB=AM−BM=(21−4)米。
28．（2022·郴州）如图是某水库大坝的横截面，坝高 CD=20m ，背水坡BC的坡度为 i1=1：1 .为了对水库大坝进行升级加固，降低背水坡的倾斜程度，设计人员准备把背水坡的坡度改为 i2=1：3 ，求背水坡新起点A与原起点B之间的距离.（参考数据： 2≈1.41 ， 3≈1.73 .结果精确到0.1m）
【答案】解：在 Rt△BCD 中，∵背水坡BC的坡度 i1=1：1 ，
∴CDBD=1 ，
∴BD=CD=20(m) .
在 RtΔACD 中，∵背水坡AC的坡度 i2=1：3 ，
∴CDAD=13 ，
∴AD=3CD=203(m) ，
∴AB=AD−BD=203−20≈14.6(m) .
答：背水坡新起点A与原起点B之间的距离约为14.6m.
【解析】【分析】根据背水坡BC的坡度可得BD=CD=20m，根据背水坡AC的坡度可得AD=3CD=203m，然后根据AB=AD-BD进行计算.
29．（2022·通辽）某型号飞机的机翼形状如图所示，根据图中数据计算AB的长度（结果保留小数点后一位，3≈1.7）.
【答案】解：如图，延长BA交CE的垂线DG于点F，AC，DF交于点G，则四边形DFBE是矩形，
∵∠FDB=45°，
∴DF=FB，
∴四边形DFBE是正方形，
∴BF=EB=14，
∵∠DCG=90°−60°=30°，AF∥CD，
∴∠FAG=∠DCG=30°，
Rt△CDG中，DG=tan∠DCG⋅CD=33×20=2033，
∴GF=DF−DG=14−2033，
Rt△AFG中，AF=FGtan∠FAG=FGtan30°=14−203333=143−20，
∴AB=BF−AF=14−143+20=34−143≈9.8米．
【解析】【分析】在Rt△CDG中，求出DG的值，在Rt△AFG中，得出AF的值，由此得解。
30．（2022·锦州）如图，一艘货轮在海面上航行，准备要停靠到码头C，货轮航行到A处时，测得码头C在北偏东60°方向上．为了躲避A，C之间的暗礁，这艘货轮调整航向，沿着北偏东30°方向继续航行，当它航行到B处后，又沿着南偏东70°方向航行20海里到达码头C．求货轮从A到B航行的距离（结果精确到0.1海里．参考数据：sin50°≈0.766，cs50°≈0.643，tan50°≈1.192）．
【答案】解：过B作BD⊥AC于D，
由题意可知∠ABE=30°，∠BAC=30°，则∠C=180°-30°-30°-70°=50°，
在Rt△BCD中，∠C=50°，BC=20(海里)，
∴BD= BCsin50°≈20×0.766=15.32(海里)，
在Rt△ABD中，∠BAD=30°，BD=15.32(海里)，
∴AB=2BD=30.64≈30.6(海里)，
答：货轮从A到B航行的距离约为30.6海里．
【解析】【分析】先利用解直角三角形求出BD的长，再利用含30°角的直角三角形的性质可得AB的长。
31．（2022·呼和浩特）“一去紫台连朔漠，独留青冢向黄昏”，美丽的昭君博物院作为著名景区现已成为外地游客到呼和浩特市旅游的打卡地．如图，为测量景区中一座雕像AB的高度，某数学兴趣小组在D处用测角仪测得雕像顶部A的仰角为30°，测得底部B的俯角为10°．已知测角仪CD与水平地面垂直且高度为1米，求雕像AB的高．（用非特殊角的三角函数及根式表示即可）
【答案】解：如图，过点C作CE⊥AB于E，则四边形CDBE是矩形，
∴CD=BE=1，
Rt△ACE中，tan∠ACE=AECE=tan30°=33，
∴AE=33CE，
Rt△EBC中，tan∠ECB=EBEC=tan10°，
∵EB=CD=1
∴EC=EBtan10°=1tan10°，
∴AB=AE+EB=33⋅tan10°+1tan10°=3+33⋅tan10°米
答：雕像AB的高为3+33⋅tan10°米
【解析】【分析】过点C作CE⊥AB于E，则四边形CDBE是矩形， CD=BE=1，在Rt△ACE中，tan∠ACE=AECE=tan30°=33，AE=33CE，利用锐角三角函数的定义，在Rt△EBC中，tan∠ECB=EBEC=tan10°，由EB=CD=1可得EC=EBtan10°=1tan10°，则AB=AE+EB=33⋅tan10°+1tan10°=3+33⋅tan10°米。
32．（2022·绥化）如图所示，为了测量百货大楼CD顶部广告牌ED的高度，在距离百货大楼30m的A处用仪器测得∠DAC=30°；向百货大楼的方向走10m，到达B处时，测得∠EBC=48°，仪器高度忽略不计，求广告牌ED的高度．（结果保留小数点后一位）
（参考数据：3≈1.732，sin48°≈0.743，cs48°≈0.669，tan48°≈1.111）
【答案】解：根据题意有AC=30m，AB=10m，∠C=90°，
则BC=AC-AB=30-10=20，
在Rt△ADC中，DC=AC×tan∠A=30×tan30∘=103，
在Rt△BEC中，EC=BC×tan∠EBC=20×tan48∘，
∴DE=EC−DC=20×tan48∘−103，
即DE=20×tan48∘−103≈20×1.111−10×1.732=4.9
故广告牌DE的高度为4.9m．
【解析】【分析】先利用锐角三角函数求出DC=AC×tan∠A=30×tan30∘=103，EC=BC×tan∠EBC=20×tan48∘，再利用线段的和差可得DE=EC−DC=20×tan48∘−103，最后计算即可。
33．（2022·泸州）如图，海中有两小岛C，D，某渔船在海中的A处测得小岛C位于东北方向，小岛D位于南偏东30°方向，且A，D相距10 nmile.该渔船自西向东航行一段时间后到达点B，此时测得小岛C位于西北方向且与点B相距82 nmile.求B，D间的距离（计算过程中的数据不取近似值）.
【答案】解：如图，过点D作DE⊥AB于点E，
根据题意可得，∠BAC=∠ABC=45°，∠BAD=60°，AD=10 nmile，BC=82 nmile.
在Rt△ABC中，AC=BC=82，
∴AB=2BC=16(nmile)，
在Rt△ADE中，AD=10 nmile，∠EAD=60°，
∴DE=AD•sin60°=10×32=53(nmile)，
AE=12AD=5 (nmile)，
∴BE=AB-AE=11(nmile)，
∴BD=DE2+BE2=14(nmile)，
答：B，D间的距离为14nmile.
【解析】【分析】过点D作DE⊥AB于点E，根据题意可得：∠BAC=∠ABC=45°，∠BAD=60°，AD=10 nmile，BC=82nmile，则AB=2BC=16(nmile)，根据三角函数的概念可得DE、AE，由BE=AB-AE可得BE，然后根据勾股定理计算即可.
34．（2022·泗洪模拟）如图所示，玫瑰家园小区有甲、乙两栋居民楼，小明在甲居民楼的楼顶B处观测乙居民楼楼底D处的俯角是30°，观测乙居民楼楼顶C处的仰角为15°，已知甲居民楼的高为10m，求乙居民楼的高.（参考数据：2=1.414，3=1.732，结果精确到0.1m）
【答案】解：如图：分别过C、B作CF⊥BD，BE⊥DC，垂足分别为E、F，则DE=AB=10，
∵在Rt△BDE中，∠DBE=30°，AB=10
∴BD=20，AD=103
∵在Rt△CFB中，∠CBF=∠DBE+∠CBE=45°，
∴CF=BF
∵在Rt△CFD中，∠DCF=30°，
∴tan∠DCF=DFCF=tan30°=33，CF=BF=3DF
∴BD=BF+DF=3DF+DF=20，即DF=10(3−1)
∴CD=2DF=20(3−1)
解得CD=20(3−1)≈14.6m
∴乙居民楼的高14.6m.
【解析】【分析】 分别过C、B作CF⊥BD，BE⊥DC，垂足分别为E、F，则DE=AB=10， 根据含30°的直角三角形的性质可得BD=20 ，易得∠CBF=∠BCF=45°，可得CF=BF，根据解直角三角形可求出 CF=BF=3DF ，由BD=DF+BF可求出DF的长，从而由CD=2DF求出答案.
35．（2022·邵阳）如图，一艘轮船从点A处以30km/ℎ的速度向正东方向航行，在A处测得灯塔C在北偏东60°方向上，继续航行1ℎ到达B处，这时测得灯塔C在北偏东45°方向上，已知在灯塔C的四周40km内有暗礁，问这艘轮船继续向正东方向航行是否安全？并说明理由.（提示：2≈1.414，3≈1.732）
【答案】解：过点C作CD⊥AB，垂足为D.如图所示：
根据题意可知∠BAC=90°−60°=30°，∠DBC=90°-45°=45°，AB=30×1=30（km），
在Rt△BCD中，∠CDB=90°，∠DBC=45°，
tan∠DBC=CDBD，即CDBD=1
∴CD=BD
设BD=CD=xkm，
在Rt△ACD中，∠CDA=90°，∠DAC=30°，
∴tan∠DAC=CDAD，即x30+x=33
解得x=153+15≈40.98，
∵40.98km>40km
∴这艘船继续向东航行安全.
【解析】【分析】过点C作CD⊥AB，垂足为D，易知∠BAC=30°，∠DBC=45°，AB=30×1=30km，利用 ∠DBC 的正切三角函数的概念可得CD=BD，设BD=CD=xkm，根据 ∠DAC 的正切三角函数的概念并结合特殊锐角三角函数值可得x，然后与40km进行比较即可判断.
36．（2022·达州）某老年活动中心欲在一房前3m高的前墙（ AB ）上安装一遮阳篷 BC ，使正午时刻房前能有2m宽的阴影处（ AD ）以供纳凉，假设此地某日正午时刻太阳光与水平地面的夹角为63.4°，遮阳篷 BC 与水平面的夹角为10°，下图为侧面示意图，请你求出此遮阳篷 BC 的长度（结果精确到0.1m）.（参考数据： sin10°≈0.17 ， cs10°≈0.98 ， tan10°≈0.18 ； sin63.4°≈0.89 ， cs63.4°≈0.45 ， tan63.4°≈2.00 ）
【答案】解：如图，过点C作CF⊥AD的延长线于点F，
∵∠A=90°，∠BEC=90°，
∴四边形AECF为矩形，
∴AF=EC，AE=FC，
设AE=FC=a米，
∴在Rt△CFD中，∠CDF=63.4°，
∴DF=CFtan63.4°=a2米，
∵AD=2米，AB=3米
∴AF=EC=（a2+2）米，BE=（3-a）米，
∴在Rt△CEB中，∠BCE=10°，
∴tan10°=BEEC=3−aa2+2=0.18，
整理，解得：a≈2.4，
∴BE=3-2.4=0.6，
∴BC=BEsin10°=≈3.5.
答：遮阳棚BC的长度约为3.5米.
【解析】【分析】过点C作CF⊥AD的延长线于点F，易得四边形AECF为矩形，则AF=EC，AE=FC，设AE=FC=a米，在Rt△CFD中，∠CDF=63.4°，求得DF=a2米，继而得AF=EC=（a2+2）米，BE=（3-a）米，在Rt△CEB中，∠BCE=10°，由正切函数关系得3−aa2+2=0.18，整理，解得：a≈2.4，则BE=3-2.4=0.6，再由正弦函数关系求出BC的长即可.
37．（2022·四川）去年，我国南方菜地一处山坡上一座输电铁塔因受雪灾影响，被冰雪从C处压折，塔尖恰好落在坡面上的点B处，造成局部地区供电中断，为尽快抢通供电线路，专业维修人员迅速奔赴现场进行处理在B处测得BC与水平线的夹角为45°，塔基A所在斜坡与水平线的夹角为30°，A、B两点间的距离为16米，求压折前该输电铁塔的高度（结果保留根号）．
【答案】解：如图，
∵BD∥EF，
∴∠ABD=∠E=30°，
在Rt△ADB中，
∴AD=12AB=8米，BD=ABcs∠ABD=83米，
∵∠CBD=45°，
在Rt△BDC中，
∴CD=BD=83米，BC=BDcs45°=86米，
∴AD+CD+BC=（8+83+86）米，
答： 压折前该输电铁塔的高度为 （8+83+86）米.
【解析】【分析】过点B作BD⊥AC于点D，在Rt△ABD和Rt△BCD中，分别解直角三角形求出AD、BD、CD、BC的长，根据线段和差即可求出结果.
38．（2022·和平模拟）如图，斜立于地面的木杆AB，从点C处折断后，上半部分BC倒在地上，杆的顶部B恰好接触到地面D处，测得∠ACD=60°，∠ADC=37°，折断部分CD长5.73米，求木杆AB的长度（结果保留整数）．参考数据：sin37°≈0.6，cs37°≈0.8，tan37°≈0.75，3≈1.73．
【答案】解：如图，过点A作AE⊥CD于点E，
∴∠AEC=∠AED=90°，
由题意可知∠ACD=60°，∠ADC=37°，CD=5.73，
在Rt△AED中，tan∠ADC=AEDE=tan37°，
∴DE=AEtan37°，
∵在Rt△AEC中，tan∠ACD=AECE=tan60°，sin∠ACD=AEAC=sin60°，
∴CE=AEtan60°=AE3=33AE，AC=AEsin60°=AE32=233AE，
∵DC=CE+DE=5.73，
∴33AE+AEtan37°=5.73，
∴解得AE≈3，
∴AB=AC+CD=233AE+CD=23+5.73≈9m．
答：木杆AB的长度约是9米．
【解析】【分析】过点A作AE⊥CD于点E，在Rt△AEC中，tan∠ACD=AECE=tan60°，sin∠ACD=AEAC=sin60°，得出CE、AC的值，从而求出DC的长，再得出AE的值，代入求解即可。
39．（2022·郯城模拟）如图所示，某人通过定滑轮拉动静止在水平面上的箱子，开始时与物体相连的绳和水平面间的夹角为37°，拉动一段距离后，绳与水平面间的夹角为53°，绳子的自由端竖直向下移动了3米，求箱子移动的距离．（绳子伸缩不计）（参考数据：sin37°=35，sin53°=45，tan37°=34，tan53°=43）
【答案】解：由题意得：OA比OB长3米．
设：OB=x米，则OA=(x+3)米，
∵AB⊥OC，
∴在Rt△AOC中：
∴sin∠OAC=sin37°=OCOA=35，
∴OC=35OA=35(x+3)，
同理：OC=45OB=45x，
∴35(x+3)=45x，
∴x=9，OA=12，
∴OB=9，OA=12．tan∠OAC=tan37°=OCAC=34=45xAC，
∴AC=16x15，
∴AC=9.6，
同理：BC=5.4．
∴AB=AC−BC=9.6−5.4=4.2米．
答：箱子移动了4.2米．
【解析】【分析】 设OB=x米，则OA=(x+3)米，在Rt△AOC中，由sin∠OAC=sin37°=OCOA=35可得 OC=35OA=35(x+3)，同理可得OC=45OB=45x，据此建立关于x方程并解之即得OB、OA的长，然后再求出AC、BC的长，由AB=AC-BC即可求解.
40．（2022·温江模拟）如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，求河流的宽度BC.（结果精确到1m；参考数据：sin67°≈0.92，cs67°≈0.39，tan67°≈2.30，3≈1.73）
【答案】解：如图，AD⊥BC，垂足为点D，
在Rt△ACD中，∠C=30°，AD=46，
∴tan30°=46CD，
∴CD=4633=463≈79.58，
在Rt△ABD中，∠ABD=67°，AD=46，
∴tan67°=46BD，
∴BD=46tan67°≈462.30=20，
∴BC=CD-BD=79.58-20≈60.
答：河流的宽度BC约为60m.
【解析】【分析】根据AD⊥BC，垂足为点D，分别在Rt△ACD、Rt△ABD中利用三角函数的定义求出CD、BD的长，则可得出BC长，即河流在B、C两地的宽度.