数学九年级下册第24章 圆24.3 圆周角24.3.2 圆内接四边形作业课件ppt

这是一份数学九年级下册第24章 圆24.3 圆周角24.3.2 圆内接四边形作业课件ppt，共36页。PPT课件主要包含了答案呈现，答案B，答案D，点易错等内容，欢迎下载使用。

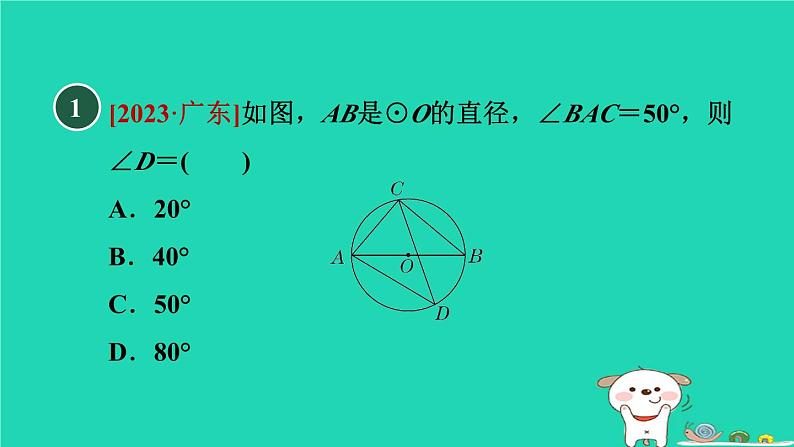
[2023·广东]如图，AB是⊙O的直径，∠BAC＝50°，则∠D＝(　　)A．20° B．40° C．50° D．80°
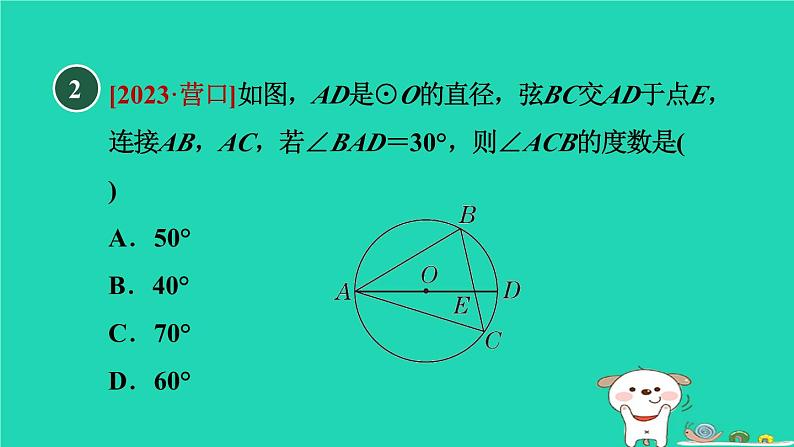
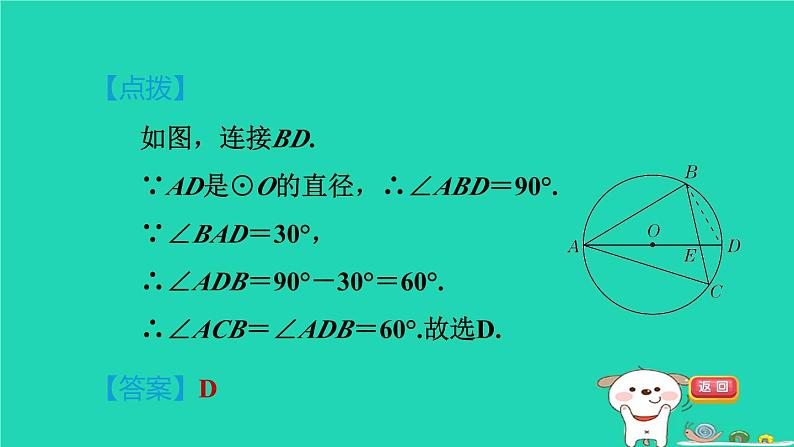
[2023·营口]如图，AD是⊙O的直径，弦BC交AD于点E，连接AB，AC，若∠BAD＝30°，则∠ACB的度数是(　　)A．50° B．40° C．70° D．60°
如图，连接BD. ∵AD是⊙O的直径，∴∠ABD＝90°.∵∠BAD＝30°，∴∠ADB＝90°－30°＝60°.∴∠ACB＝∠ADB＝60°.故选D.
[2023·黄冈]如图，在⊙O中，直径AB与弦CD相交于点P，连接AC，AD，BD，若∠C＝20°，∠BPC＝70°，则∠ADC＝(　　)A．70° B．60° C．50° D．40°
连接AB.∵∠AOB＝90°，∴AB是⊙P的直径，∴∠ACB＝90°.
[2022·日照]一圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工人师傅用直角尺作如图所示的测量，测得AB＝12 cm，BC＝5 cm，则圆形镜面的半径为________．
∴AD＝OD＝OA，即△OAD为等边三角形．∴∠OAD＝60°.∴∠CAD＝∠CAB＋∠OAD＝30°＋60°＝90°.②当AD(D′)与AC在直径AB的同侧时，易知△OAD′为等边三角形，则∠OAD′＝60°，∴∠CAD′＝∠OAD′－∠CAB＝60°－30°＝30°.综上，∠CAD＝30°或90°.故选D.
在圆中根据已知弦长和弦的一个端点作这条弦时，往往有两条，分别位于已知的两侧，本题易对弦的位置未分类讨论而致错．
[2022·广东]如图，四边形ABCD内接于⊙O，AC为⊙O的直径，∠ADB＝∠CDB.
(1)试判断△ABC的形状，并给出证明；
(1)求线段AB的长及∠ABO的大小．
(2)在⊙C上是否存在一点P，使得△POB是等腰三角形？若存在，求∠BOP的度数；若不存在，请说明理由．
【解】存在．如图，作OB的垂直平分线MN，交⊙C于点M，N，交OB于点D，连接OM，BM，ON，BN.
易得MN必过点C，即MN是⊙C的直径．∵MN垂直平分OB，∴△OBM，△OBN都是等腰三角形．∴点M，N均符合点P的要求．∵MN是⊙C的直径，∴∠MON＝90°.∵∠BMO＝∠BAO＝90°－30°＝60°，∴△OBM是等边三角形．∴∠BOM＝60°.∴∠BON＝∠MON－∠BOM＝90°－60°＝30°.故存在符合条件的点P，∠BOP的度数为60°或30°.
如图，已知ED为⊙O的直径且ED＝4，A(不与E，D重合)为⊙O上一个动点，线段AB经过点E，且EA＝EB，F为⊙O上一点，∠FEB＝90°，BF的延长线与AD的延长线交于点C.
(1)求证：△EFB≌△ADE；
【证明】如图，连接FA.∵∠FEB＝90°，∴EF⊥AB.∴∠FEA＝90°. ∵BE＝AE，∴BF＝AF.∵∠FEA＝90°，∴AF是⊙O的直径．∴AF＝DE.∴BF＝ED.∵DE是⊙O的直径，∴∠EAD＝90°.∴Rt△EFB≌Rt△ADE(HL)．
(2)当点A在⊙O上移动时，直接写出四边形FCDE的最大面积为多少．
【解】四边形FCDE的最大面积为8.
如图，以△ABC的边AC为直径作⊙O，交BC边于点D，过点C作CE∥AB交⊙O于点E，连接AD，DE，∠B＝∠ADE.
(1)求证：AC＝BC；
【证明】∵∠ADE＝∠ACE，∠ADE＝∠B，∴∠B＝∠ACE.∵CE∥AB，∴∠BAC＝∠ACE.∴∠B＝∠BAC.∴AC＝BC.
(2)若tan B＝2，CD＝3，求AB和DE的长．