初中数学沪科版九年级下册25.2.2 由三视图确定几何体及计算作业课件ppt

这是一份初中数学沪科版九年级下册25.2.2 由三视图确定几何体及计算作业课件ppt，共30页。PPT课件主要包含了答案呈现，答案B，正六棱柱，∶27等内容，欢迎下载使用。

[2023·仙桃]如图是一个立体图形的三视图，该立体图形是(　　)A．三棱柱 B．圆柱 C．三棱锥 D．圆锥
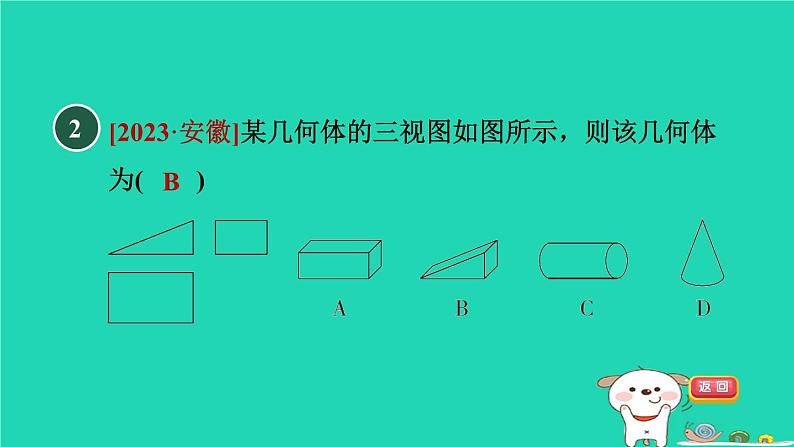
[2023·安徽]某几何体的三视图如图所示，则该几何体为(　　)
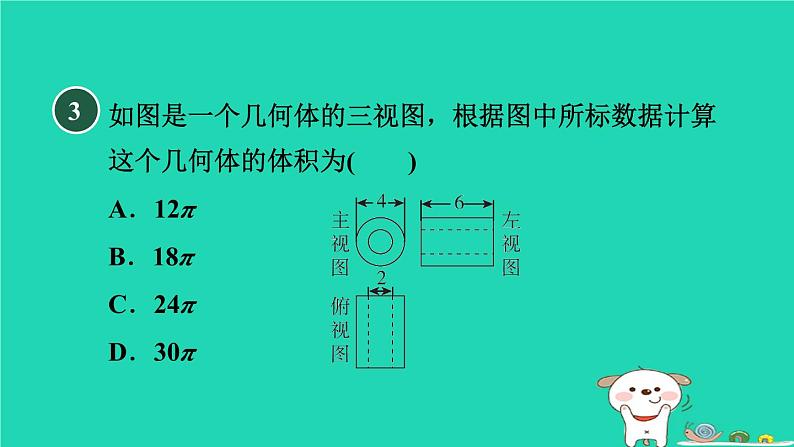
如图是一个几何体的三视图，根据图中所标数据计算这个几何体的体积为(　　)A．12π B．18π C．24π D．30π
由三视图可得该几何体是空心圆柱，其小圆半径是1，大圆半径是2，则大圆面积为π×22＝4π，小圆面积为π×12＝π，故这个几何体的体积为6×4π－6×π＝24π－6π＝18π.故选B.
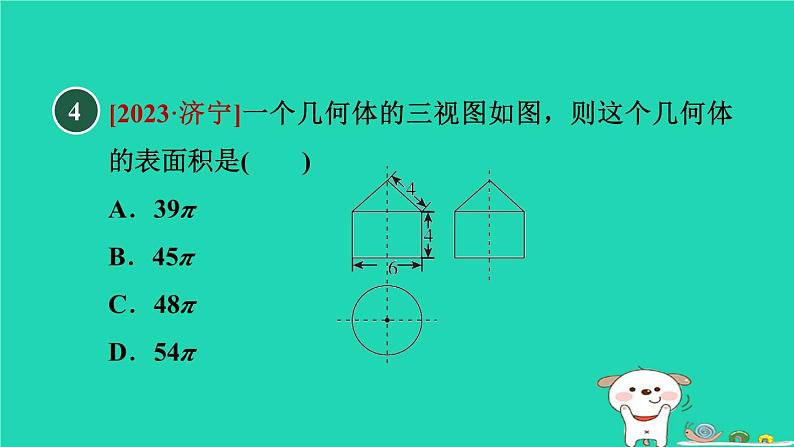
[2023·济宁]一个几何体的三视图如图，则这个几何体的表面积是(　　)A．39π B．45π C．48π D．54π
[2023·河北]如图①，一个2×2的平台上已经放了一个棱长为1的正方体，要得到一个几何体，其主视图和左视图如图②，平台上至少还需再放这样的正方体(　　)A．1个 B．2个 C．3个 D．4个
[2022·黑龙江]如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是(　　)A．7 B．8 C．9 D．10
一个几何体是由若干个棱长为3 cm的小正方体搭成的，从左面和上面看到的几何体的形状如图所示．(1)该几何体最少由________个小正方体搭成，最多由________个小正方体搭成．
该几何体最少(如图①)由2＋1＋3＋1＋1＋1＝9(个)小正方体搭成，最多(如图②)由2＋2＋3＋3＋3＋1＝14(个)小正方体搭成．
(2)将该几何体的形状固定好．①求该几何体体积的最大值；
【解】该几何体体积的最大值为33×14＝378(cm3)．
【解】所涂油漆的面积有两种情形：如图③，涂油漆的面有2×[5＋6＋(6＋1)]＝36(个)，所涂油漆的面积为36×32＝324(cm2)．如图④，涂油漆的面有2×[6＋6＋(6＋1)]＝38(个)，所涂油漆的面积为38×32＝342(cm2)．
②若要给体积最小时的几何体的表面涂上油漆，求所涂油漆的面积．
如图是一个包装纸盒的三视图(单位：cm)．(1)该包装纸盒的几何形状是___________；
(2)画出该纸盒的平面展开图；
【解】如图所示．(答案不唯一)
(3)计算制作一个这样的纸盒所需纸板的面积．(精确到1 cm2)
[2023·徐州]两汉文化看徐州，桐桐在徐州博物馆“天工汉玉”展厅参观时了解到：玉璧、玉环为我国的传统玉器，通常为正中带圆孔的扁圆形器物，据《尔雅·释器》记载：“肉倍好，谓之璧；肉好若一，谓之环. ”如图①，“肉”指边(阴影部分) ，“好”指孔，其比例关系见图示，以考古发现来看，这两种玉器的“肉”与“好”未必符合该比例关系．
(1)若图①中两个大圆的直径相等，则璧与环的“肉”的面积之比为________；
由题图①可知璧的“肉”的面积为π×(32－12)＝8π；环的“肉”的面积为π×(32－1.52)＝6.75π，∴它们的面积之比为8π∶6.75π＝32∶27.
(2)利用圆规与无刻度的直尺，解决下列问题(保留作图痕迹，不写作法)：①图②为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图，试判断该件玉器的比例关系是否符合“肉好若一” ?
【解】如图①所示，由作图可知该件玉器的比例关系符合“肉好若一”．
②图③表示一件圆形玉坯，若将其加工成玉璧，且比例关系符合“肉倍好”，请画出内孔．
已知一个模型的三视图如图所示(单位：m)．(1)请描述这个模型的形状．
【解】此模型由两个长方体组成：上面是一个小长方体，下面是一个大长方体．
(2)制作这个模型的木料密度为360 kg/m3，则这个模型的质量是多少千克？
【解】此模型的体积为5×6×10＋2×3×1.5＝309(m3)，则该模型的质量为309×360＝111 240(kg)．
(3)如果要给这个模型刷油漆，每千克油漆可以刷4 m2，需要油漆多少千克？
【解】此模型的表面积为2×3×2＋2×1.5×2＋10×5×2＋5×6×2＋6×10×2＝298(m2)，需要油漆298÷4＝74.5(kg)．
学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如下表：
(1)当桌子上放有x个碟子时(x为正整数)，请写出此时碟子的高度(用含x的式子表示)；
【解】由题意，得x个碟子的高度为2＋1.5(x－1)＝(1.5x＋0.5)cm.
(2)分别从三个方向上看，其三视图如图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度．
【解】由三视图可知共有12个碟子，∴叠成一摞后的高度为1.5×12＋0.5＝18.5(cm)．