初中数学苏科版八年级下册10.1 分式学案

这是一份初中数学苏科版八年级下册10.1 分式学案，文件包含第10章分式教师版苏科版docx、第10章分式学生版苏科版docx等2份学案配套教学资源，其中学案共25页， 欢迎下载使用。

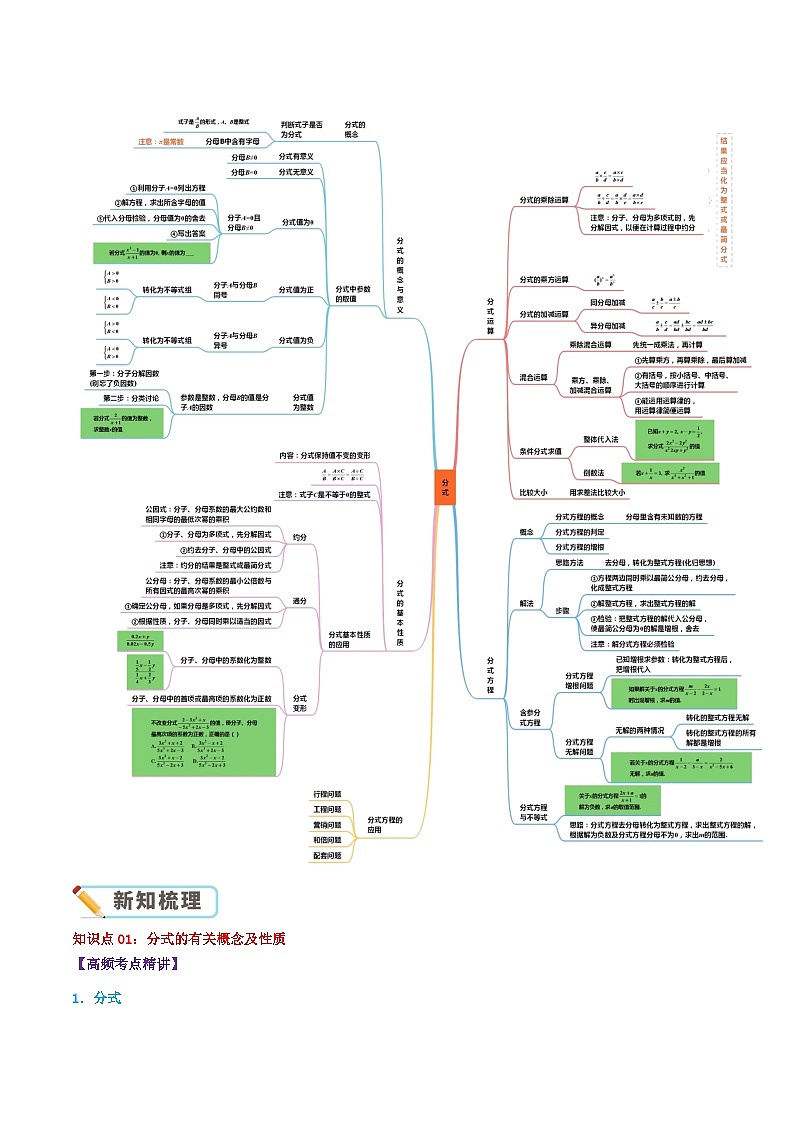
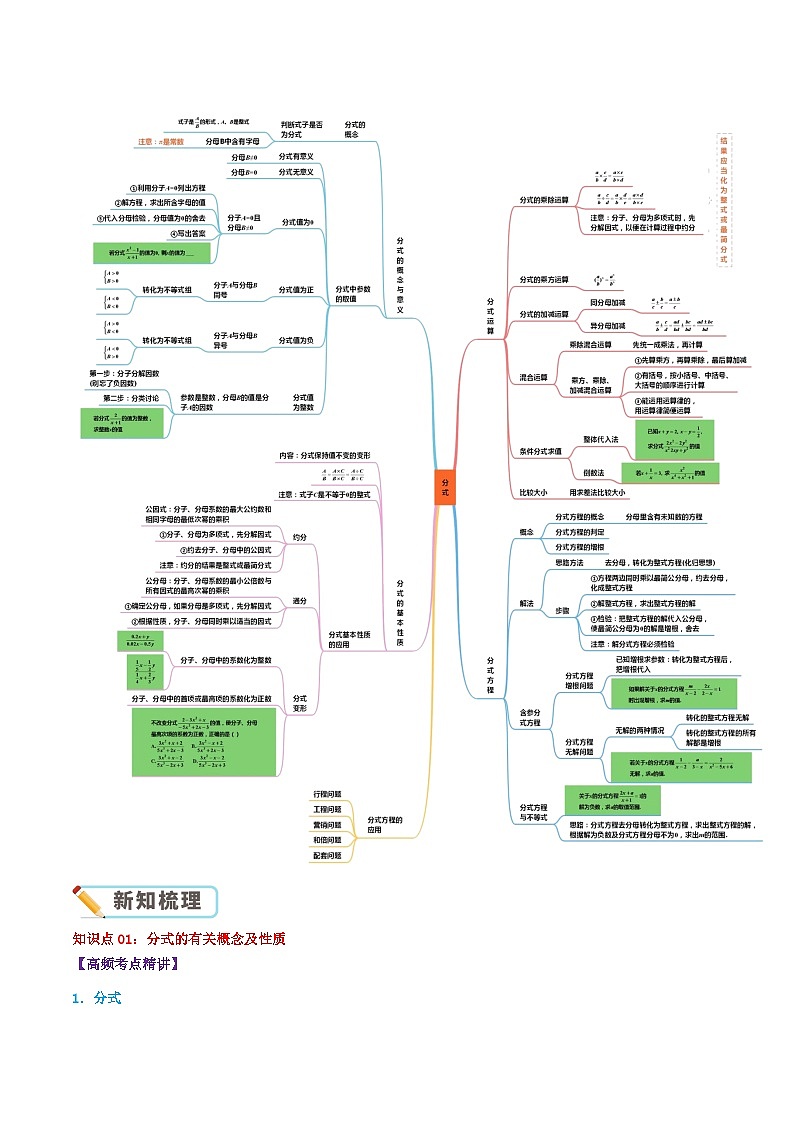
1. 理解分式的概念，能求出使分式有意义、分式无意义、分式值为0的条件.
2．了解分式的基本性质，掌握分式的约分和通分法则．
3．掌握分式的四则运算．
4．结合分析和解决实际问题，讨论可以化为一元一次方程的分式方程，掌握这种方程的解法，体会解方程中的化归思想．
知识点01：分式的有关概念及性质
【高频考点精讲】
1．分式
一般地，如果A、B表示两个整式，并且B中含有字母，那么式子叫做分式.其中A叫做分子，B叫做分母.
【易错点剖析】分式中的分母表示除数，由于除数不能为0，所以分式的分母不能为0，即当B≠0时，分式才有意义.
2.分式的基本性质
（M为不等于0的整式）.
3．最简分式
分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式，要进行约分化简.
知识点02：分式的运算
【高频考点精讲】
1．约分
利用分式的基本性质，把一个分式的分子和分母的公因式约去，不改变分式的值，这样的分式变形叫做分式的约分.
2．通分
利用分式的基本性质，使分子和分母同乘适当的整式，不改变分式的值，把异分母的分式化为同分母的分式，这样的分式变形叫做分式的通分．
3．基本运算法则
分式的运算法则与分数的运算法则类似,具体运算法则如下:
（1）加减运算
；同分母的分式相加减，分母不变，把分子相加减.
；异分母的分式相加减，先通分，变为同分母的分式，再加减.
（2）乘法运算 ，其中是整式，.
两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母.
（3）除法运算 ，其中是整式，.
两个分式相除，把除式的分子和分母颠倒位置后，与被除式相乘.
（4）乘方运算
分式的乘方，把分子、分母分别乘方.
4.分式的混合运算顺序
先算乘方，再算乘除，最后加减，有括号先算括号里面的.
知识点03：分式方程
【高频考点精讲】
1．分式方程的概念
分母中含有未知数的方程叫做分式方程．
2．分式方程的解法
解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程．
3．分式方程的增根问题
增根的产生：分式方程本身隐含着分母不为0的条件，当把分式方程转化为整式方程后，方程中未知数允许取值的范围扩大了，如果转化后的整式方程的根恰好使原方程中分母的值为0，那么就会出现不适合原方程的根－－－增根.
【易错点剖析】因为解分式方程可能出现增根，所以解分式方程必须验根．验根的方法是将所得的根带入到最简公分母中，看它是否为0，如果为0，即为增根，不为0，就是原方程的解.
知识点04：分式方程的应用
列分式方程解应用题与列一元一次方程解应用题类似，但要稍复杂一些．解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节，从而正确列出方程，并进行求解.
检测时间：120分钟 试题满分：100分 难度系数：0.53
一．选择题（共10小题，满分20分，每小题2分）
1．（2分）（2023秋•汉阳区期末）已知分式（a，b为常数）满足表格中的信息，则下列结论中错误的是（ ）
A．b＝﹣4B．a＝2C．m＝﹣10D．a＝﹣2
解：当x＝2时，＝0，
∴4+b＝0，
解得b＝﹣4，
故A不符合题意；
当x＝﹣2时，无解，
∴﹣2﹣a＝0，
解得a＝﹣2，
故B符合题意；D不符合题意；
∴分式为，
当x＝m时，＝3，
解得m＝﹣10，
故C不符合题意；
故选：B．
2．（2分）（2023秋•如皋市期末）我们把形如（a，b不为零），且两个解分别为x1＝a，x2＝b的方程称为“十字分式方程”．如，为“十字分式方程”，其可转化为，则x1＝1，x2＝3．若k＞2时，关于x的“十字分式方程”的两个解分别为x1，x2，且x1＜x2，则的值为（ ）
A．B．C．﹣2D．2
解：原方程变为x+1+＝（k+1）+（k﹣1），
∴x1+1＝k﹣1，x2+1＝k+1，
∴x1＝k﹣2，x2＝k，
∴＝＝．
故选：A．
3．（2分）（2023秋•江汉区期末）绿化队原来用漫灌方式浇绿地，a天用水m吨，现改用喷灌方式，可使这些水多用3天，则现在比原来每天节约用水吨数是（ ）吨．
A．B．C．D．
解：由题意得，原来每天用水的吨数为（吨），现在每天用水的吨数为（吨），
∴现在比原来每天节约用水吨数是（）吨．
故选：A．
4．（2分）（2023秋•大连期末）甲乙两地相距400千米，一辆汽车从甲地开往乙地，实际每小时比原计划多行驶12km，结果提前1小时到达．设这辆汽车原计划的速度为x千米/时，根据题意可列方程为（ ）
A．＝+1B．＝+1
C．+1＝D．+1＝
解：设原来的平均速度为x千米/时，
由题意得，＝+1，
故选：A．
5．（2分）（2023秋•惠州期末）已知，则的值为（ ）
A．B．C．D．
解：∵，
∴设a＝2k，b＝5k，
∴
＝
＝
＝
＝．
故选：A．
6．（2分）（2023秋•商丘期末）下列各分式中，是最简分式的是（ ）
A．B．
C．D．
解：A．是最简分式；
B．＝＝x﹣y，不符合题意；
C．＝＝，不符合题意；
D．＝，不符合题意；
故选：A．
7．（2分）（2023秋•昌黎县期末）关于x的分式方程有增根，则m的值是（ ）
A．﹣2B．3C．﹣3D．2
解：
去分母，得x﹣3＝m，
移项，得x＝m+3．
∵关于x的分式方程有增根，
∴m+3﹣1＝0，
∴m＝﹣2．
故选：A．
8．（2分）（2023秋•纳溪区期末）已知关于x的分式方程＝1的解是非负数，则m的取值范围是（ ）
A．m≥1B．m≤1C．m≥﹣1且m≠0D．m≥﹣1
解：分式方程去分母得：m＝x﹣1，
即x＝m+1，
由分式方程的解为非负数，得到
m+1≥0，且m+1≠1，
解得：m≥﹣1且m≠0，
故选：C．
9．（2分）（2023春•宣汉县校级期末）已知关于x的分式方程的解为正数，关于y的不等式组，恰好有三个整数解，则所有满足条件的整数a的和是（ ）
A．1B．3C．4D．6
解：关于x的分式方程解为x＝2a﹣1，
∵x解为正数，
∴2a﹣1＞0，
∴a＞，
关于y的不等式组解为，
∵y恰有三个整数解，
∴0＜≤1，
∴﹣1＜a≤3，
分式方程中，x≠3，
∴2a﹣1≠3，
∴a≠2，
综上所述：＜a≤3，
∴满足条件的整数a为：1、3，
则所有满足条件的整数a的和是4．
故选：C．
10．（2分）（2022秋•河间市校级期末）已知关于x的一元一次不等式组的解集为x＞2，且关于y的分式方程的解为正整数，则所有满足条件的所有整数a的和为（ ）
A．2B．5C．6D．9
解：∵不等式组的解集为x＞2，
∴a﹣2≤2．
∴a≤4．
关于y的分式方程＝1﹣的解为y＝．
∵y＝3是原分式方程的增根，
∴≠3．
∴a≠3．
∵关于y的分式方程＝1﹣的解为正整数，
∴为正整数．
∴a＝2，4，7．
∵a≤4，
∴a＝2，4．
∴所有满足条件的所有整数a的和为：2+4＝6．
故选：C．
二．填空题（共10小题，满分20分，每小题2分）
11．（2分）（2023秋•崇川区期末）若关于x的方程+＝5的解为正数，则m的取值范围是 m＜且m≠ ．
解：+＝5，
去分母，得x﹣m﹣2m＝5（x﹣1），
∴x﹣3m＝5x﹣5，
∴﹣4x＝﹣5+3m．
∴x＝．
∵方程的解为正数，且x≠1．
∴＞0，且≠1．
∴m＜且m≠．
故答案为：m＜且m≠．
12．（2分）（2023秋•海淀区校级期末）若关于x的方程＝8的解为x＝，则m＝ 4 ．
解：分式方程去分母得：mx+1＝8x，
根据题意将x＝代入方程得：m+1＝2，
解得：m＝4．
故答案为：4
13．（2分）（2023秋•柘城县期末）若三角形的三边为4、7、x且x是关于x的方程的解，则a的范围为 4＜a＜36，且a≠24． ．
解：由题意得3＜x＜11，
解方程，
得x＝，
∴3＜＜11，且≠8，
解得4＜a＜36，且a≠24，
故答案为：4＜a＜36，且a≠24．
14．（2分）（2023秋•川汇区期末）分式与的最简公分母是 2a2b2c ．
解：题中两分式的最简公分母即求两分式分母的最小公倍数，即为2a2b2c．故答案为2a2b2c．
15．（2分）（2023秋•渝中区校级期末）若整数a使关于x的不等式组无解，且使关于y的分式方程有非负整数解，则满足条件的a的值之和为 0 ．
解：，解得：
，
由不等式组无解可知，﹣2+3a≤a+2，
解得：a≤2，
∵，
∴ay+5＝﹣3y+15，
∴（a+3）y＝10，
∴当a+3≠0时，即a≠﹣3时，y＝，
∵y≠5，
∴y＝≠5，
解得：a+3≠2，
∵分式方程有非负整数解，即a+3＝1或a+3＝5或a+3＝10，
解得：a＝﹣2或a＝2或a＝7，
∵a≤2，
∴a＝﹣2或a＝2，
∴﹣2+2＝0．
故答案为：0．
16．（2分）（2023秋•长沙期末）已知关于x的分式方程，则该分式方程的解为 x＝3 ．
解：方程两边都乘以x（x﹣1）得：2x＝3（x﹣1），
解得：x＝3，
检验：∵当x＝3时，x（x﹣1）≠0，
∴x＝3是原方程的解，
故答案为：x＝3．
17．（2分）（2023秋•旌阳区期末）若分式的值为零，则x的值为 3 ．
解：依题意得：3﹣|x|＝0且x+3≠0，
解得x＝3．
故答案为：3．
18．（2分）（2023秋•綦江区期末）若整数m既能使关于x的不等式组有解，也能使关于y的分式方程 有整数解，则整数m的值为 ﹣1 ．
解：解关于x的不等式组得：，
∵不等式组有解，
∴m﹣3＜﹣1，
解得：m＜2，
解关于y的分式方程 得：y＝，
∵y≠3，m≠2，
∴≠3，m≠2，
∴m≠1且m≠2，
∵为整数，且m为整数，
∴m＝﹣1，
∴整数m的值为﹣1．
故答案为：﹣1．
19．（2分）（2023秋•江汉区期末）若关于x的分式方程﹣＝1无解，则m的值为 ﹣2或1 ．
解：去分母得：x2﹣mx﹣3x+3＝x2﹣x，
解得：（2+m）x＝3，
由分式方程无解，得到2+m＝0，即m＝﹣2或x＝＝1，即m＝1，
综上，m的值为﹣2或1．
故答案为：﹣2或1
20．（2分）（2022春•衡阳县期末）若关于x的一元一次不等式组的解集为x≥5，且关于y的分式方程+＝﹣1有非负整数解，则符合条件的所有整数a的和为 ﹣2 ．
解：，
解不等式①得：x≥5，
解不等式②得：x＞a+2，
∵解集为x≥5，
∴a+2＜5，
∴a＜3；
分式方程两边都乘以（y﹣2）得：y﹣a＝﹣（y﹣2），
解得：y＝，
∵分式方程有非负整数解，
∴≥0，为整数，
∴a≥﹣2，a为偶数，
∵≠2，
∴a≠2，
综上所述，﹣2≤a＜3且a≠2且a为偶数，
∴符合条件的所有整数a的数有：﹣2，0，
和为﹣2+0＝﹣2．
故答案为：﹣2．
三．解答题（共8小题，满分60分）
21．（6分）（2023秋•潮南区校级期末）计算：
（1）因式分解：5x2﹣45；
（2）解方程：．
解：（1）5x2﹣45；
＝5（x2﹣9）
＝5（x+3）（x﹣3）；
（2），
去分母，得12﹣3（x+3）＝x﹣3．
解这个方程，得x＝．
检验：当x＝时，（x+3）（x﹣3）≠0，
∴x＝是原方程的解．
22．（6分）（2023秋•南昌期末）先化简，再求值：，其中x＝3．
解：原式＝
＝•
＝，
当 x＝3时，
原式＝．
23．（8分）（2023秋•昆明期末）乡村振兴，交通先行．近年以来，某市高质量推进“四好”农村公路建设，着力打通农村交通基础设施．某村准备修一条5400米长的道路，在修建600米后，由于采用新的修建技术，这样每天修建长度是原来的2倍，结果共用15天完成了全部任务，求原来每天修建道路多少米．
解：设原来每天修建道路x米，则采用新的修建技术后每天修建道路2x米，
根据题意得：+＝15，
解得：x＝200，
经检验，x＝200是所列方程的解，且符合题意．
答：原来每天修建道路200米．
24．（8分）（2023秋•武都区期末）2023年第31届世界大学生夏季运动会将在成都举办，与吉祥物“蓉宝”有关的纪念品现已上市．某商店计划今年购进A，B两种“蓉宝”纪念品若干件，订购A种“蓉宝”纪念品花费6000元，订购B种“蓉宝”纪念品花费3200元，其中A种纪念品的订购单价比B种纪念品的订购单价多20元，并且订购A种纪念品的数量是B种纪念品数量的1.25倍．
（1）求商店订购A种纪念品和B种纪念品分别是多少件？
（2）若商店一次性购买A，B纪念品共60件，要使总费用不超过3000元，最少要购买多少件B种纪念品？
解：（1）设商店订购B种纪念品x件，则订购A种纪念品1.25x件，
根据题意，得，
解得x＝80，
经检验，x＝80是原方程的根，且符合题意，
1.25×80＝100（件），
答：商店订购A种纪念品100件，B种纪念品80件；
（2）设购买m件B种纪念品，
A种商品的单价为6000÷100＝60（元），B种商品的单价为60﹣20＝40（元），
根据题意，得60（60﹣m）+40m≤3000，
解得m≥30，
答：最少购买30件B种纪念品．
25．（8分）（2023秋•浏阳市期末）“春节”是我国最传统、最热闹的节日．计划由甲、乙两个工厂一起生产一批2024龙年春晚吉祥物形象“龙辰辰”．已知甲工厂每天生产的数量是乙工厂每天生产数量的1.5倍，两工厂各生产2400个该吉祥物时，甲工厂比乙工厂少用2天．
（1）求甲乙两工厂每天各生产多少个吉祥物？
（2）已知甲乙两工厂生产该吉祥物每天的费用分别是1800元和1000元，计划由两个工厂合作生产15000个这种吉祥物，由于时间的限制，甲乙两工厂同时开始生产，同时结束，那么一共需要支付多少资金？
解：（1）设乙工厂每天生产x个吉祥物，则甲工厂每天生产1.5x个吉祥物，
由题意得：﹣＝2，
解得：x＝400，
经检验，x＝400是原方程的解，且符合题意，
∴1.5x＝1.5×400＝600，
答：甲工厂每天生产600个吉祥物，乙工厂每天生产400个吉祥物；
（2）甲乙两工厂同时生产，一天可生产吉祥物：400+600＝1000（个），
甲乙两工厂同时生产的天数为：＝15（天），
∴一共需要支付的资金为：（1800+1000）×15＝42000（元），
答：一共需要支付42000元资金．
26．（8分）（2023秋•滨海新区期末）小刚到离家1200米的电影院看电影，到电影院时发现钱包丢在家里，此时距电影放映还有25分钟，于是他立即步行（匀速）回家，在家拿钱包用了2分钟，然后骑自行车（匀速）返回电影院，已知小刚骑自行车的速度是步行速度的2.5倍，小刚骑自行车到电影院比他从电影院步行到家少用了9分钟．
（1）小刚步行的速度是每分钟多少米？
（2）小刚能否在电影放映前赶到电影院？
解：（1）设小刚步行的速度是x米/分钟，
由题意得：，
解得：x＝80，
经检验，x＝80是原分式方程的解，且符合题意，
答：小刚步行的速度是每分钟80米．
（2）∵，
∴小刚能在电影放映开始前赶到电影院．
27．（8分）（2023秋•乌拉特前旗期末）八年级学生去距离学校10km的博物馆参观，一部分学生骑自行车先走，过了20min后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度．
解：设骑车学生的速度为xkm/h，则汽车的速度为2xkm/h，
由题意得：﹣＝，
解得：x＝15，
经检验：x＝15是原方程的解，且符合题意，
答：骑车学生的速度为15km/h．
28．（8分）（2023•乌鲁木齐一模）某商店五月份销售A型电脑的总利润为4320元，销售B型电脑的总利润为3060元，且销售A型电脑数量是销售B型电脑的2倍，已知销售一台B型电脑比销售一台A型电脑多获利50元．
（1）求每台A型电脑和B型电脑的利润；
（2）该商店计划一次购进两种型号的电脑共100台且全部售出，其中B型电脑的进货量不超过A型电脑的2倍，该商店购进A型、B型电脑各多少台，才能使销售总利润最大？最大利润是多少？
解：（1）设每台A型电脑的利润为x元，则每台B型电脑的利润为（x+50）元，
根据题意得＝×2，
解得x＝120．
经检验，x＝120是原方程的解，
则x+50＝170．
答：每台A型电脑的利润为120元，每台B型电脑的利润为170元；
（2）设购进A型电脑a台，这100台电脑的销售总利润为y元，
据题意得，y＝120a+170（100﹣a），
即y＝﹣50a+17000，
100﹣a≤2a，
解得a≥33，
∵y＝﹣50a+17000，
∴y随a的增大而减小，
∵a为正整数，
∴当a＝34时，y取最大值，此时y＝﹣50×34+17000＝15300．
即商店购进34台A型电脑和66台B型电脑，才能使销售总利润最大，最大利润是15300x的取值
2
m
﹣2
分式的值
0
3
无解