

2024年陕西省安高新第一中学中考第二次模拟考试数学试题(无答案)
展开1.的绝对值是( )
A.B.2024C.D.
2.如图,一块直角三角板的直角顶点放在直尺的一边上,如果,那么的度数是( )
A.20°B.25°C.30°D.45°
3.党的二十大报告指出,我国建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系,教育普及水平实现历史性跨越,基本养老保险覆盖十亿四千万人,基本医疗保险参保率稳定在百分之九十五,将数据1040000000用科学记数法表示为( )
A.B.C.D.
4.下列运算正确的是( )
A.B.
C.D.
5.在下列条件中,能够判定为菱形的是( )
A.B.C.D.
6.在平面直角坐标系中,将直线沿轴向右平移2个单位后恰好经过原点,则的值为( )
A.B.2C.D.3
7.如图,内接于是的直径,若,则的度数是( )
A.B.C.D.
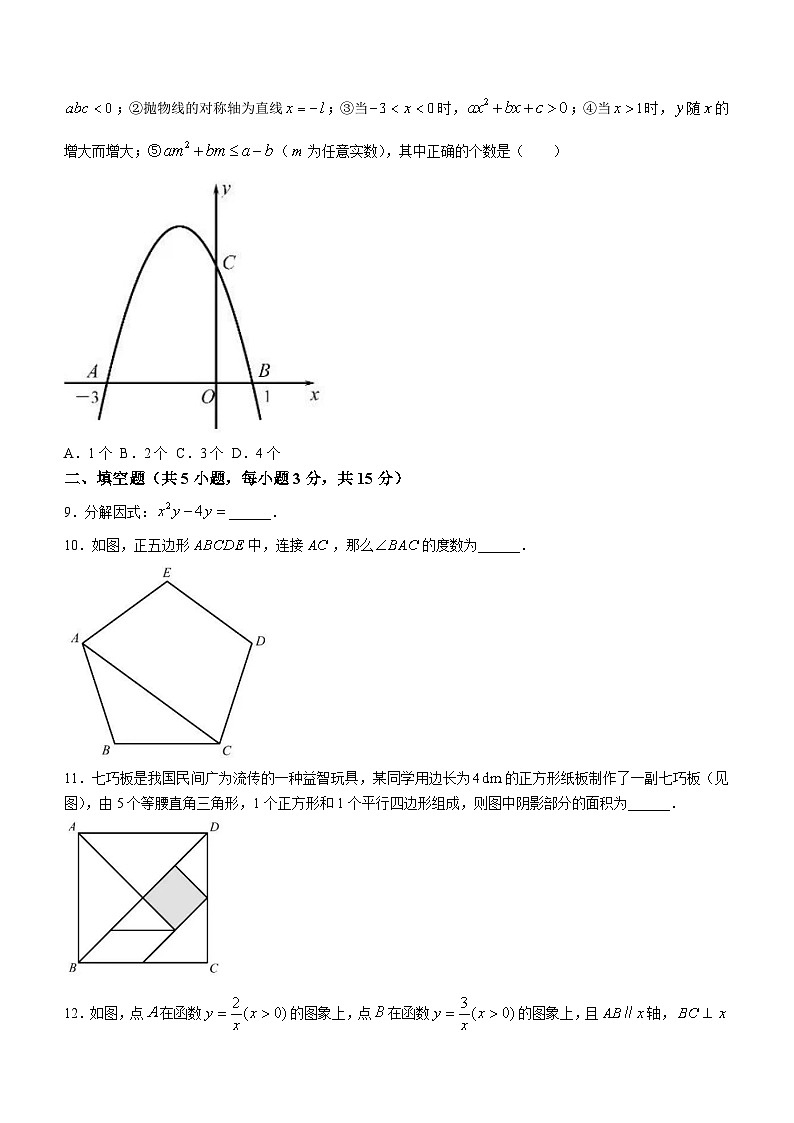
8.如图,抛物线与轴交于点和点,与轴交于点.下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,随的增大而增大;⑤(为任意实数),其中正确的个数是( )
A.1个B.2个C.3个D.4个
二、填空题(共5小题,每小题3分,共15分)
9.分解因式:______.
10.如图,正五边形中,连接,那么的度数为______.
11.七巧板是我国民间广为流传的一种益智玩具,某同学用边长为的正方形纸板制作了一副七巧板(见图),由5个等腰直角三角形,1个正方形和1个平行四边形组成,则图中阴影部分的面积为______.
12.如图,点在函数的图象上,点在函数的图象上,且轴,轴丁点,则四边形的面积为______.
13.在中,为上动点,连接,以为邻边作平行四边形,连接,则的最小值为______.
三、解答题(共13小题,共81分,解答题应写出过程)
14.(本题满分5分)
计算:;
15.(本题满分5分)
解不等式组:
16.(本题满分5分)
化简:.
17.(本题满分5分)
如图,在锐角中,,请在边上找一点,使.(尺规作图,保留作图痕迹,不写作法)
18.(本题满分5分)
如图,,垂足分别为.求证:.
19.(本题满分5分)
如图,在平面直角坐标系中,已知的三个顶点坐标分别是.
(1)请画出关于轴对称的;
(2)若与关于原点成中心对称,请直接写出点的对应点的坐标______.
20.(本题满分5分)
二十四节气是中国古代一种用来指导农事的补充历法,在国际气象界被誉为“中国的第五大发明”,并位列联合国教科文组织人类非物质文化遗产代表作名录,小明和小亮对二十四节气非常感兴趣,在课间玩游戏时,准备了四张完全相同的不透明卡片,卡片正面分别写有“A.惊蛰”“B.夏至”“C.白露”“D.霜降”四个节气,两人商量将卡片背面朝上洗匀后,从中随机抽取一张,并讲述所抽卡片上的节气的由来与习俗.
(1)小明从四张卡片中随机抽取一张卡片,抽到“A.惊蛰”的概率是______.
(2)小明先从四张卡片中随机抽取一张,小亮再从剩下的卡片中随机抽取一张,请用列表或画树状图的方法,求两人都没有抽到“B.夏至”的概率.
21.(本题满分6分)
某食用油的沸点温度远高于水的沸点温度,小聪想用刻度不超过100℃的温度计测算出这种食用油沸点的温度,在老师的指导下,他在锅中倒入一些这种食用油均匀加热,并每隔10s测量一次锅中油温,得到的数据记录如下:
(1)小聪在直角坐标系中描出了表中数据对应的点,经老师介绍,在这种食用油达到沸点前,锅中油温y(单位:℃)与加热的时间t(单位:s)符合初中学习过的某种函数关系,可能是______函数关系(请选填“正比例”、“一次”、“二次”、“反比例”);
(2)根据以上判断,求y关于t的函数表达式;
(3)当加热110s时,油沸腾了,请推算沸点的温度.
22.(本题满分5分)
4月23日是世界读书日,为了解学生的阅读喜好,丰富学校图书资源,某校将课外书籍设置了四类:文学类、科技类、艺术类、其他类,随机抽查了部分学生,要求每名学生从中选择自己最喜欢的一类,将抽查结果绘制成如图统计图(不完整),请根据图中信息解答下列问题:
(1)直接写出扇形统计图中m的值为______;
(2)请将条形统计图补充完整;
(3)若该校共有1200名学生,根据抽查结果,试估计全校最喜欢“文学类”书籍的学生人数.
23.(本题满分7分)
2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达4点时,从位于地面C处的雷达站测得AC的距离是8km,仰角为30°;10s后飞船到达B处,此时测得仰角为45°,求飞船从A处到B处的平均速度.(结果精确到0.1km/s,参考数据:)
24.(本题满分8分)
如图,是的直径,与相切于点,点在上,连接,且,点在线段的延长线上.
(1)求证:;
(2)若,求的长.
25.(本题满分8分)
已知抛物线经过点,与轴的交点为.
(1)求该抛物线的函数表达式;
(2)若点是该抛物线上一点,且位于其对称轴右侧,对称轴与轴交于点,过点作轴,垂足为.若,求出点的坐标.
26.(本题满分12分)
问题提出
(1)如图1,已知是面积为的等边三角形,是的平分线,则的长为问题探究
(2)如图2,在中,为的中点,点分別在边上,且,证明:.
问题解决
(3)如图3,李叔叔准备在一块空地上修建一个矩形花园,然后将其分割种植三种不同的花卉.按照他的分割方案,点分别在上,连接分别在上,连接,其中四边形种植玫瑰,和种植那余香,剩下的区域种植康乃馨,根据实际需要,要求种植玫瑰的四边形的面积为,为了节约成本,矩形花园的面积是否存在最小值?若存在,请求出矩形的最小面积,若不存在,请说明理由.
图1 图2 图3
时间
0
10
20
30
40
油温
10
30
50
70
90
陕西省西安高新第一中学2023-2024学年九年级上学期月考数学试题(无答案): 这是一份陕西省西安高新第一中学2023-2024学年九年级上学期月考数学试题(无答案),共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024年陕西省西安高新第一中学中考第一次模拟考试数学试卷: 这是一份2024年陕西省西安高新第一中学中考第一次模拟考试数学试卷,共7页。
2024年陕西省西安市西安高新第一中学中考二模数学试题: 这是一份2024年陕西省西安市西安高新第一中学中考二模数学试题,共4页。












