江苏省连云港市灌云县西片2023-2024学年七年级下学期3月月考数学试题(含答案)

这是一份江苏省连云港市灌云县西片2023-2024学年七年级下学期3月月考数学试题(含答案)，共7页。试卷主要包含了如图所示，∠1和∠2是，下列运算正确的是，若2n×2m＝26，则m+n＝等内容，欢迎下载使用。

一．选择题（共8小题）
1．如图所示，∠1和∠2是（ ）
A．同位角B．内错角C．同旁内角D．邻补角
2．下列三条线段的长度，能组成三角形的是（ ）
A．3，3，6B．5，6，12C．2，5，7D．6，7，8
（第1题图） （第3题图）
3．如图，下列能判定AB∥CD的条件有（ ）
①∠B+∠BCD＝180°；②∠1＝∠2；③∠3＝∠4；④∠B＝∠5．
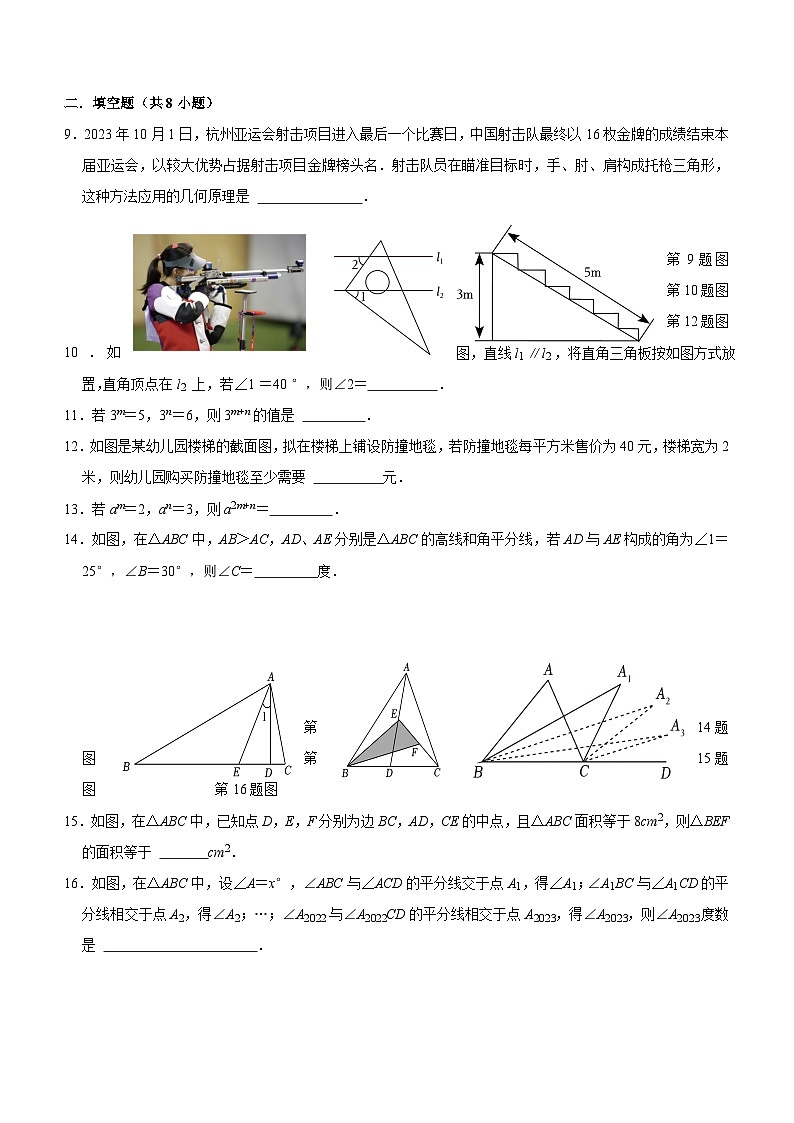
A．1个B．2个C．3个D．4个
4．下列运算正确的是（ ）
A．x3+x3＝2x6 B．（x2）4＝x6 C．x2•x4＝x6 D．（﹣2x）3＝﹣6x3
5．一个n边形的每个外角都是45°，则这个n边形的内角和是（ ）
A．1260°B．1080°C．900°D．720°
6．若2n×2m＝26，则m+n＝（ ）
A．3B．4C．5D．6
7．如图，△ABC平移到△DEF的位置，则下列说法：①AB∥DE，AD＝CF＝BE；②∠ACB＝∠DEF；③平移的方向是点C到点F的方向；④平移距离为线段BD的长．其中说法正确的有（ ）A．①②B．①③C．①④D．②④
（第7题图） （第8题图）
8．如图，AB∥EF，设∠C＝90°，那么x、y和z的关系是（ ）
A．y＝x+z B．x+y﹣z＝90° C．x+y+z＝180° D．y+z﹣x＝90°
二．填空题（共8小题）
9．2023年10月1日，杭州亚运会射击项目进入最后一个比赛日，中国射击队最终以16枚金牌的成绩结束本届亚运会，以较大优势占据射击项目金牌榜头名．射击队员在瞄准目标时，手、肘、肩构成托枪三角形，这种方法应用的几何原理是 ．
第9题图 第10题图 第12题图
10．如图，直线l1∥l2，将直角三角板按如图方式放置，直角顶点在l2上，若∠1＝40°，则∠2＝ ．
11．若3m＝5，3n＝6，则3m+n的值是 ．
12．如图是某幼儿园楼梯的截面图，拟在楼梯上铺设防撞地毯，若防撞地毯每平方米售价为40元，楼梯宽为2米，则幼儿园购买防撞地毯至少需要 元．
13．若am＝2，an＝3，则a2m+n＝ ．
14．如图，在△ABC中，AB＞AC，AD、AE分别是△ABC的高线和角平分线，若AD与AE构成的角为∠1＝25°，∠B＝30°，则∠C＝ 度．
第14题图 第15题图 第16题图
15．如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且△ABC面积等于8cm2，则△BEF的面积等于 cm2．
16．如图，在△ABC中，设∠A＝x°，∠ABC与∠ACD的平分线交于点A1，得∠A1；∠A1BC与∠A1CD的平分线相交于点A2，得∠A2；…；∠A2022与∠A2022CD的平分线相交于点A2023，得∠A2023，则∠A2023度数是 ．
三．解答题（共10小题）
17．计算：（1）x7•x5+（﹣2x3）4．（2）（b﹣a）2•（a﹣b）3+2（a﹣b）5．
18．画图并填空：如图，三角形ABC的顶点都在方格纸的格点上，每个格子的边长为1个单位长度，将三角形ABC向上平移3个单位长度，得到三角形A′B′C′．
（1）在图中作出三角形ABC边AB上的高CD；
（2）在图中画出平移后的三角形A′B′C′；
（3）三角形ABC的面积为 ；
（4）若连接AA′，CC′，则这两条线段的关系是 ．
19．将如图所示的长为1.5×102cm，宽为1.2×102cm，高为0.8×102cm的大理石运往某地用以建设革命历史博物馆．
（1）求每块大理石的体积；（结果用科学记数法表示）
（2）如果一列火车总共运送了3×104块大理石，共约重1.2×108千克，求每块大理石约重多少千克？（结果用科学记数法表示）
20．下图是东东同学完成的一道作业题，请你参考东东的方法解答下列问题．
（1）计算：①82022×（﹣0.125）2022；②（）11×（）13×（）12；
（2）若3×9n×81n＝325，请求出n的值．
21．在下面的解答中，填上适当的理由或数学式．
（一）（1）∵∠1＝ ． ∴AD∥BC ．
（2）∵∠1＝ ． ∴AB∥CD ．
（二）（1）∵a∥b ∴∠3＝ ．
（2）∵a∥b ∴∠2+∠4＝ ．
22．如图，将Rt△ABC沿BC方向平移得到Rt△DEF，其中AB＝8，BE＝8，DM＝5，求阴影部分的面积．
23．一个多边形的内角和是它外角和的2倍，求这个多边形的边数．
24．将下面的推理过程及依据补充完整．
已知：如图，AB∥CD，点E在AB上，点F在CD上，∠1＝∠2，求证：∠B＝∠C．
证明：∵∠1＝∠2（已知）∠1＝∠4（ ① ）
∴∠2＝∠4（等量代换）
∴CE∥BF（② ）
∴∠3＝∠③ （两直线平行，同位角相等）
又∵AB∥CD（已知）
∴∠3＝∠B（④ ）
∴∠B＝∠C（等量代换）
25．规定两数a，b之间的一种运算，记作（a，b）：如果ac＝b，那么（a，b）＝c．
例如：因为23＝8，所以（2，8）＝3．
（1）根据上述规定，填空：（5，25）＝ ，（﹣2，4）＝ ，（﹣3，81）＝ ；
（2）小明在研究这种运算时发现一个现象：（3n，4n）＝（3，4），他给出了如下的证明：
设（3n，4n）＝x，则（3n）x＝4n，即（3x）n＝4n．∴3x＝4，即（3，4）＝x，
∴（3n，4n）＝（3，4）．
请你尝试运用上述这种方法说明下面这个等式成立的理由．（4，7）+（4，8）＝（4，56）．
26．如图，A，B分别是∠MON两边OM，ON上的动点（均不与点O重合）．
（1）如图1，当∠MON＝58°时，△AOB的外角∠NBA，∠MAB的平分线交于点C，则∠ACB＝ °；
（2）如图2，当∠MON＝n°时，∠OAB，∠OBA的平分线交于点D，则∠ADB＝ °（用含n的式子表示）；
（3）如图3，当∠MON＝α（α为定值，0°＜α＜90°）时，BE是∠NBA的平分线，BE的反向延长线与∠OAB的平分线交于点F．随着点A，B的运动，∠F的大小会改变吗？如果不会，求出∠F的度数（用含α的式子表示）；如果会，请说明理由．
参考答案
一．选择题（共8小题）
1．C．2．D．3．C．4．C．5．B．6．D．7．B．8．B．
二．填空题（共8小题）
9．三角形具有稳定性． 10．50°． 11．30． 12．560．
13．12． 14．80． 15．2． 16．x°．
三．解答题（共10小题）
17．（1）17x12；（2）（a﹣b）5．
18．解：（1）（2）（3）8；
（4）AA′＝CC′，AA′∥CC′．
19．解：（1）1.5×102×1.2×102×0.8×102＝（1.5×1.2×0.8）×（102×102×102）
＝1.44×106（cm3）．所以每块大理石的体积为1.44×106cm3；
（2）1.2×108）÷（3×104）＝（1.2÷3）×（108÷104）＝0.4×104
＝4×103（千克）．所以每块大理石约重4×103千克．
20．解：（1）①82022×（﹣0.125）2022＝82022×0.1252022＝（8×0.125）2022＝12022＝1；
②（）11×（）13×（）12＝（）11×（）11×（）2×（）11×
＝（××）11××＝111×＝1×＝；
（2）∵3×9n×81n＝325，∴3×（32）n×（34）n＝325．∴3×32n×34n＝325．
∴31+2n+4n＝325．∴1+2n+4n＝25．∴n＝4．
21．（一）（1）解：∵∠1＝∠B，∴AD∥BC（同位角相等，两直线平行）．
故答案为：∠B；同位角相等，两直线平行．
（2）解：∵∠1＝∠D，∴AB∥CD（内错角相等，两直线平行）．
故答案为：∠D；内错角相等，两直线平行．
（二）（1）解：∵a∥b，∴∠3＝∠2．故答案为：∠2，
（2）解：∵a∥b，∴∠2+∠4＝180°．故答案为：180°．
22．解：∵直角△ABC沿BC方向平移得到直角△DEF，∴DE＝AB＝8，
∵DM＝5，∴ME＝DE﹣DM＝8﹣5＝3，
由平移可得：S阴影＝S△DEF﹣S△MEC＝S△ABC﹣S△MEC＝S梯形ABEM＝×（3+8）×8，＝44．
23．解：设这个多边形的边数是n，
根据题意得，（n﹣2）•180°＝2×360°，解得n＝6．答：这个多边形的边数是6．
24．证明：∵∠1＝∠2（已知），
∠1＝∠4（①对顶角相等），
∴∠2＝∠4，
∴CE∥BF（②同位角相等，两直线平行）．
∴∠3＝③∠C（④两直线平行，同位角相等）．
又∵AB∥CD（已知），
∴∠3＝⑤∠B（⑥两直线平行，内错角相等），
∴∠B＝∠C．
故答案为：对顶角相等；同位角相等，两直线平行；∠C，两直线平行，同位角相等；∠B；两直线平行，内错角相等．
25．解；（1）∵52＝25，（﹣2）2＝4，（﹣3）4＝81，
∴（5，25）＝2，（﹣2，4）＝2，（﹣3，81）＝4，
故答案为：2，2，4；
（2）设4x＝7，4y＝8，则4x•4y＝4x+y＝56，
∴（4，7）＝x，（4，8）＝y，（4，56）＝x+y，
∴（4，7）+（4，8）＝（4，56）．
26．解：（1）∵∠MON＝58°，
∴∠OBA+∠OAB＝122°．
∴∠NBA+∠MAB＝238°．
∵BD、AD分别为∠NBA、∠MAB的平分线，
∴∠DBA＝NBA，∠DAB＝∠MAB．
∴∠DBA+∠DAB＝×（∠NBA+∠MAB）＝90°+58°．
∴∠ADB＝180°﹣（90°+58°）＝90°﹣58°＝61°．
故答案为：61．
（2）∵∠MON＝n°，
∴∠OBA+∠OAB＝180°﹣n°．
∵BC、AC分别为∠OBA、∠OAB的平分线，
∴∠ABC＝∠OBA，∠BAC＝∠OAB，
∴∠ABC+∠BAC＝×（∠OBA+∠OAB）＝（180°﹣n°）．
∴∠ACB＝180°﹣（180°﹣n°）＝90°+n°．
故答案为：（90+n）．
（3）∠F的大小不变，∠F＝α．
理由如下：∵∠NBA﹣∠BAO＝∠MON＝α，
又BE是∠ABN的平分线，AF是∠OAB的平分线，
∴∠EBA＝∠NBA，∠BAF＝∠BAO，
∴∠F＝∠EBA﹣∠BAF＝（∠NBA﹣∠BAO）＝α．
东东的作业
计算：45×（﹣0.25）5．解：原式＝（﹣4×0.25）5＝（﹣1）5＝﹣1．