
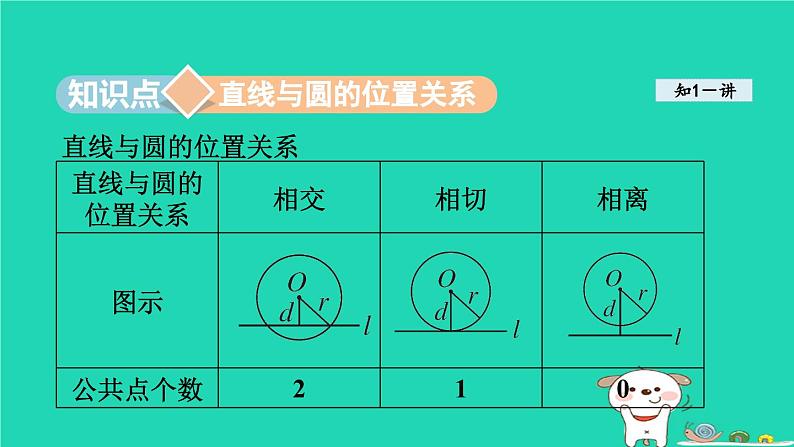
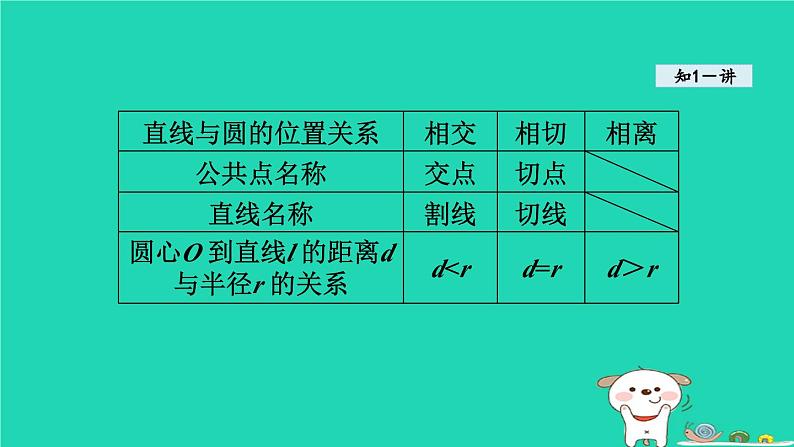



沪科版九年级下册24.4.1 直线与圆的位置关系教课ppt课件
展开直线与圆的位置关系切线性质定理切线判定定理切线长定理
易错警示1. 理解切线的定义时,要抓住关键字眼“只有一个”,避免出现“有公共点时,直线和圆相切”的错误,用动态的观点及数形结合思想来准确理解切线的定义.2. 射线、线段和圆的位置关系不能像直线一样依据交点的个数判断,要具体情况具体分析.
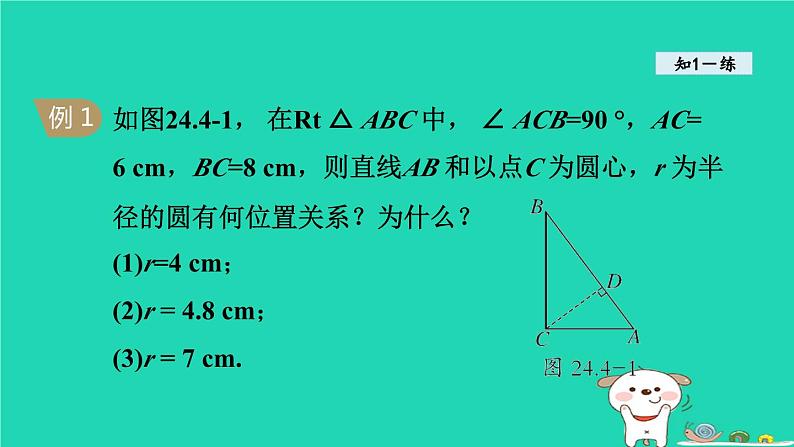
如图24.4-1, 在Rt △ ABC 中, ∠ ACB=90 °,AC=6 cm,BC=8 cm,则直线AB 和以点C 为圆心,r 为半径的圆有何位置关系?为什么?(1)r=4 cm;(2)r = 4.8 cm;(3)r = 7 cm.
解题秘方:先求出点C 到直线AB 的距离,再将其与圆的半径进行比较判断即可.
解法提醒判断直线与圆的位置关系的两种方法:1. 根据直线与圆的公共点的个数判断;2. 将圆心到直线的距离d与圆的半径r 相比较,在没有给出d 与r的具体数值的情况下,可先利用图形条件及性质求出d与r的值,再通过比较大小判断其位置关系.
1. 切线性质定理 圆的切线垂直于经过切点的半径.2. 切线的性质 (1)切线和圆只有一个公共点.(2)圆心到切线的距离等于半径.(3)圆的切线垂直于过切点的半径.(4)经过圆心且垂直于切线的直线必过切点(找切点用).(5)经过切点且垂直于切线的直线必过圆心(找圆心用).
以上(3)(4)(5)可归纳为:如果直线满足过圆心、过切点、垂直于切线这三个条件中的任意两个,那么第三个也成立.
特别提醒切线必须同时具备两个条件:1. 直线过半径的外端;2. 直线垂直于这条半径.
解题秘方:本题主要考查切线的性质、圆周角定理、勾股定理、直角三角形中30°角的性质. 得出∠ A=30°是解题关键.
解法提醒已知圆的切线时,常连接圆心和切点,得到半径垂直于切线,通过构造直角三角形来解决问题,即“见切线,连半径,得垂线”.
1. 判定定理 经过半径外端点并且垂直于这条半径的直线是圆的切线.
2. 判定方法(1)定义法:与圆有唯一公共点的直线是圆的切线;(2)数量法:圆心到直线的距离等于半径的直线是圆的切线;(3)判定定理法:经过半径外端点并且垂直于这条半径的直线是圆的切线.
特别提醒切线的判定定理与性质定理的区别:切线的判定定理是在未知相切而要证明相切的情况下使用;切线的性质定理是在已知相切而要推得其他的结论时使用,它们是一个互逆的过程,不要混淆.
[中考·湖州]如图24.4-3,已知BC 是⊙ O 的直径,AC切⊙ O 于点C,AB 交⊙ O 于点D,E 为AC 的中点,连接DE.
解法提醒看到切线,就想作过切点的半径;看到直径,就想直径所对的圆周角是直角;看到切线的判定,就想:(1)若已知直线与圆的公共点,则采用判定定理法,其基本思路是:当已知点在圆上时,连接过这点的半径,证明这条半径与直线垂直即可,即有切点,连半径,证垂直;(2)若未知直线与圆有公共点,则采用数量关系法,其基本思路是:过圆心作直线的垂线段,证明垂线段的长等于圆的半径,即无切点,作垂直,证半径.
(1)若AD=DB,OC=5,求切线AC 的长;
解题秘方:构造直径所对的圆周角,利用直径所对的圆周角是直角求解;
解:如图24.4-3,连接CD.∵ BC 是⊙ O 的直径,∴∠ BDC=90°,即CD ⊥ AB.∵ AD=DB,∴ AC=BC=2OC=10.
(2)求证:DE 是⊙ O 的切线.
解题秘方:利用“有切点,连半径,证垂直”求解.
如图24.4-4,在Rt △ ABC 中,∠ B=90°,∠ BAC的平分线交BC 于点D,以点D 为圆心,DB 长为半径作⊙ D.求证:AC 与⊙ D 相切.
解题秘方:利用“无切点,作垂线,证半径”判定圆的切线.
证明:如图24.4-4,过点D 作DF ⊥ AC 于点F.∵∠ B=90°,∴ DB ⊥ AB.又∵ AD 平分∠ BAC,∴ DF=DB.∴ AC 与⊙ D 相切.
1. 切线长切线上一点到切点之间的线段长叫做这点到圆的切线长.2. 切线长定理过圆外一点作圆的两条切线,两条切线长相等,圆心与这一点的连线平分两条切线的夹角.
3. 示例 如图24.4-5 是切线长定理的一个基本图形,可以直接得到结论:(1)PO ⊥ AB;(2)OA ⊥ AP,OB ⊥ BP;(3)AP=BP;(4)∠ 1= ∠ 2= ∠ 3= ∠ 4;(5)AD=BD;(6)AC = BC等.
特别提醒经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点所连的两条线段相等.
如图24.4-6,PA,PB,DE 分别切⊙ O 于点A,B,C,点D 在PA 上,点E 在PB 上.
解题秘方:根据切线长的定义,判断出PA,PB,DA,DC,EC,EB 的长都是切线长,再利用切线长定理,找到相等关系.
(1)若PA=10,求△ PDE 的周长;
解: ∵ PA,PB,DE 分别切⊙ O 于点A,B,C,∴ PA=PB,DA=DC,EC=EB.∴ PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20,即△ PDE 的周长为20.
(2)若∠ P=50°,求∠ DOE 的度数.
解:如图24.4-6,连接OA,OC,OB.∵ PA,PB,DE 分别切⊙ O 于点A,B,C,∴ OA ⊥ PA,OB ⊥ PB,OC ⊥ DE.∴∠ DAO= ∠ EBO=90°.∴∠ P+ ∠ AOB=180°.∴∠ AOB=180°-50°=130°.
图解如图24.4-7, 利用切线长定理,可将求△ PDE 的周长转化为求PA 与PB 的和.
初中数学沪科版九年级下册24.4.2 切线的判定与性质教案配套ppt课件: 这是一份初中数学沪科版九年级下册<a href="/sx/tb_c102905_t3/?tag_id=26" target="_blank">24.4.2 切线的判定与性质教案配套ppt课件</a>,共20页。PPT课件主要包含了没有公共点,个公共点,d5cm,二切线的性质定理,于是可得,应用格式,解得m≤2,又∵⊙O的半径为2等内容,欢迎下载使用。
初中沪科版24.4.2 切线的判定与性质课文配套ppt课件: 这是一份初中沪科版<a href="/sx/tb_c102905_t3/?tag_id=26" target="_blank">24.4.2 切线的判定与性质课文配套ppt课件</a>,共18页。PPT课件主要包含了1什么叫做切线,一切线的判定定理,①连接OP,几何语言,切线的判定方法,已知半径证垂直,已知垂直证半径等内容,欢迎下载使用。
沪科版九年级下册24.4.3 切线长定理备课课件ppt: 这是一份沪科版九年级下册<a href="/sx/tb_c102906_t3/?tag_id=26" target="_blank">24.4.3 切线长定理备课课件ppt</a>,共19页。PPT课件主要包含了一切线长定理,连接OP,PAPB,∠OPA∠OPB,几何语言,拓展延伸等内容,欢迎下载使用。













