第7章 平面图形的认识（二）（章末复习）-2023-2024学年七年级数学下册同步精品课件+分层练习（苏科版）

这是一份第7章 平面图形的认识（二）（章末复习）-2023-2024学年七年级数学下册同步精品课件+分层练习（苏科版），共48页。

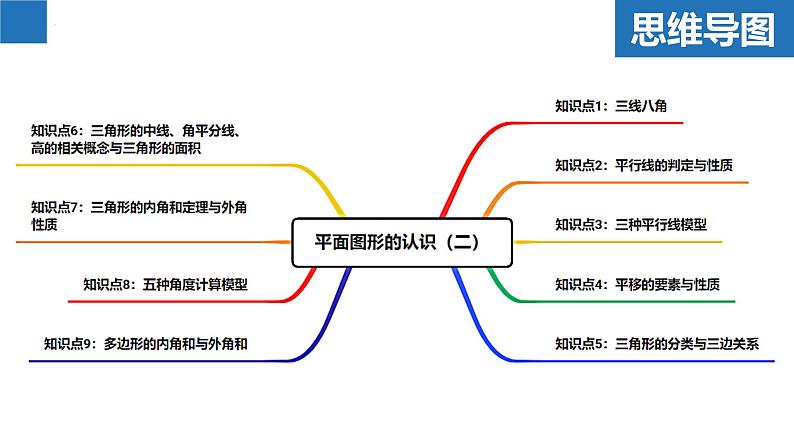
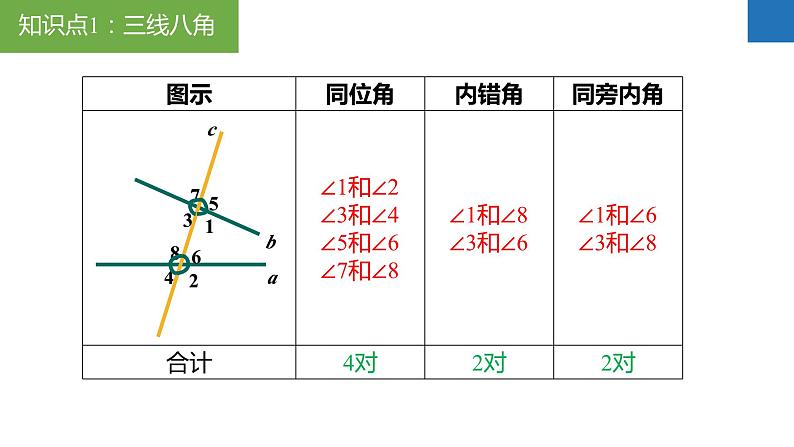
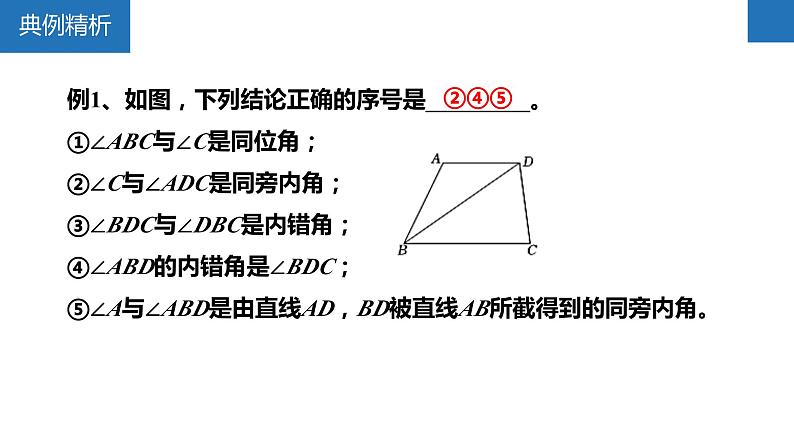
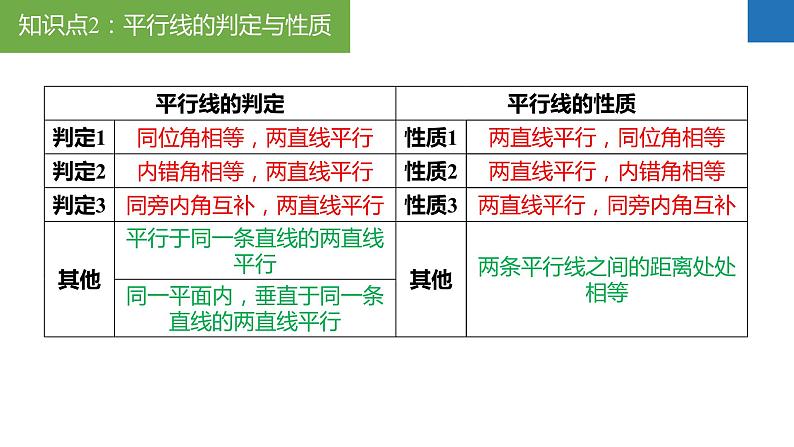
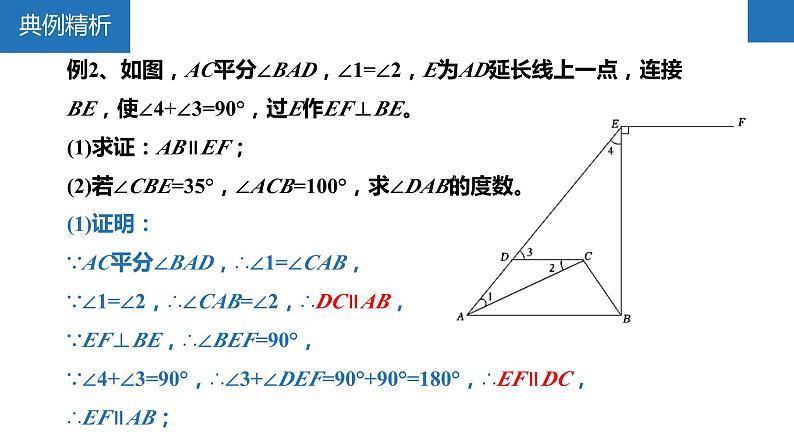
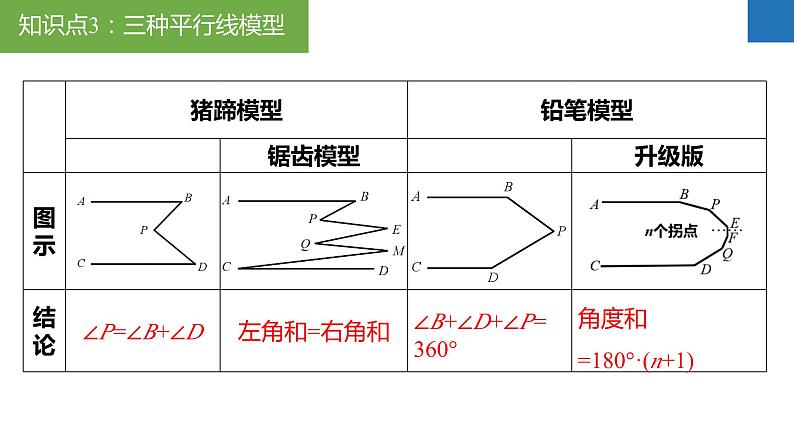
第7章平面图形的认识（二）章末复习思维导图例1、如图，下列结论正确的序号是_________。①∠ABC与∠C是同位角；②∠C与∠ADC是同旁内角；③∠BDC与∠DBC是内错角；④∠ABD的内错角是∠BDC；⑤∠A与∠ABD是由直线AD，BD被直线AB所截得到的同旁内角。②④⑤例2、如图，AC平分∠BAD，∠1=∠2，E为AD延长线上一点，连接BE，使∠4+∠3=90°，过E作EF⊥BE。(1)求证：AB∥EF；(2)若∠CBE=35°，∠ACB=100°，求∠DAB的度数。(1)证明：∵AC平分∠BAD，∴∠1=∠CAB，∵∠1=∠2，∴∠CAB=∠2，∴DC∥AB，∵EF⊥BE，∴∠BEF=90°，∵∠4+∠3=90°，∴∠3+∠DEF=90°+90°=180°，∴EF∥DC，∴EF∥AB；例2、如图，AC平分∠BAD，∠1=∠2，E为AD延长线上一点，连接BE，使∠4+∠3=90°，过E作EF⊥BE。(1)求证：AB∥EF；(2)若∠CBE=35°，∠ACB=100°，求∠DAB的度数。(2)解：∵EF∥AB，∴∠ABE=∠BEF=90°，∵∠CBE=35°，∴∠ABC=55°，∵∠ACB=100°，∴∠CAB=180°-100°-55°=25°，∵AC平分∠BAD，∴∠DAB=50°。例3、【问题背景】：同学们，观察小猪的猪蹄，你会发现一个熟悉的几何图形，我们就把这个图形的形象称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系。【问题探究】：(1)如图1，AB∥CD，E为AB、CD之间一点，连接BE、DE，得到∠BED与∠B、∠D之间的数量关系，并说明理由；【类比迁移】：(2)请你利用上述“猪蹄模型”得到的结论或解题方法，完成下面的问题：如图2，直线AB∥CD，若∠B=23°，∠G=35°，∠D=25°，求∠BEG+∠GFD的度数；【灵活应用】：(3)如图3，直线AB∥CD，若∠E=∠B=60°，∠F=85°，求∠D的度数。【问题探究】：(1)如图1，AB∥CD，E为AB、CD之间一点，连接BE、DE，得到∠BED与∠B、∠D之间的数量关系，并说明理由；解：(1)∠BED=∠B+∠D，理由如下：如图，过点E作EP∥AB，∴∠B=∠BEP，∵AB∥CD，∴CD∥EP，∴∠D=∠DEP，∵∠BED=∠BEP+∠DEP，∴∠BED=∠B+∠D；【类比迁移】：(2)请你利用上述“猪蹄模型”得到的结论或解题方法，完成下面的问题：如图2，直线AB∥CD，若∠B=23°，∠G=35°，∠D=25°，求∠BEG+∠GFD的度数；(2)如图，过点G作GM∥AB，由(1)可得：∠BEG=∠B+∠EGM，∵AB∥CD，∴GM∥CD，由(1)可得：∠GFD=∠FGM+∠D，∵∠B=23°，∠EGF=35°，∠D=25°，∴∠BEG+∠GFD=∠B+EGM+∠FGM+∠D=∠B+∠D+∠EGF=23°+25°+35°=83°；【灵活应用】：(3)如图3，直线AB∥CD，若∠E=∠B=60°，∠F=85°，求∠D的度数。(3)如图，设AB与EF相交于点N，∵∠B=60°，∠F=85°，∴∠BNF=180°-∠B-∠F=35°，∴∠ANE=∠BNF=35°，∵AB∥CD，∴由(1)可得：∠DEN=∠ANE+∠D，∴∠D=∠DEN-∠ANE=60°-35°=25°。N平移的方向与距离例4-1、如图，在三角形ABC中，BC=8cm。将三角形ABC沿BC所在直线向右平移，所得图形对应为三角形DEF，若要使AD=3CE成立，则平移的距离是________cm。6或12解：①当点E在点B、点C之间时，∵AD=BE=BC-CE=3CE，∴CE=2cm，∴AD=6cm，即平移的距离是6cm；②当点E移点C右侧时，∵AD=BE=BC+CE=3CE，∴CE=4cm，∴AD=12cm，即平移的距离是12cm。例4-2、如图，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的小路（图中阴影部分），余下部分为绿化，小路的宽为2m，则绿化的总面积是________cm。560解：由题意可得：(30-2)(22-2)=560(m2)。如果任意两条线段的长度之和大于第三条线段的长度，那么这三条线段能围成三角形；精简版——只要，那么这三条线段能围成三角形。例5、如图，将四根长度分别为3cm，5cm，7cm，8cm的木条钉成一个四边形木架，扭动它，它的形状会发生改变，在变化过程中，点B和点D之间的距离可能是（　　）A．1cm B．4cm C．9cm D．12cmC解：如图，连接BD，在△ABD中，7cm-5cm∠B。(1)如图1，若AD⊥BC于点D，∠B=40°，∠C=60°，求∠EAD的度数；(2)如图1，根据(1)的解答过程，猜想并写出∠B、∠C、∠EAD之间的数量关系且说明理由；(3)小明继续探究，如图2在线段AE上任取一点P，过点P作PD⊥BC于点D，请直接写出∠B、∠C、∠EPD之间的数量关系。在△ABC中，AE平分∠BAC，∠C>∠B。(1)如图1，若AD⊥BC于点D，∠B=40°，∠C=60°，求∠EAD的度数；在△ABC中，AE平分∠BAC，∠C>∠B。(2)如图1，根据(1)的解答过程，猜想并写出∠B、∠C、∠EAD之间的数量关系且说明理由；在△ABC中，AE平分∠BAC，∠C>∠B。(3)小明继续探究，如图2在线段AE上任取一点P，过点P作PD⊥BC于点D，请直接写出∠B、∠C、∠EPD之间的数量关系。例8-1、如图1的图形我们把它称为“8字形”。(1)如图1，求证：∠A+∠B=∠C+∠D；(2)如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC=36°，∠ADC=16°，求∠P的度数；(3)如图3，直线AP平分∠BAD，CP平分∠BCD的外角∠BCE，请直接写出∠P与∠B、∠D的数量关系。(1)如图1，求证：∠A+∠B=∠C+∠D；(1)证明：∵∠A+∠B+∠AOB=180°，∠C+∠D+∠COD=180°，又∠AOB=∠COD，∴∠A+∠B=∠C+∠D；(2)如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC=36°，∠ADC=16°，求∠P的度数；(2)解：∵AP、CP分别平分∠BAD、∠BCD，∴∠BAP=∠DAP，∠BCP=∠DCP，由(1)的结论可得：∠P+∠BCP=∠B+∠BAP①，∠P+∠DAP=∠ADC+∠DCP②，①+②得：2∠P+∠BCP+∠DAP=∠B+∠BAP+∠DCP+∠ADC，∴2∠P=∠ABC+∠ADC，∴2∠P=36°+16°=52°，解得：∠P=26°；(3)如图3，直线AP平分∠BAD，CP平分∠BCD的外角∠BCE，请直接写出∠P与∠B、∠D的数量关系。例8-2、如图1所示的图形，像我们常见的学习用品——圆规。我们不妨把这样图形叫做“规形图”，请发挥你的聪明才智，解决以下问题：(1)观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；(2)请你直接利用以上结论，解决以下三个问题：①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A=50°，直接写出∠ABX+∠ACX的结果；②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE=50°，∠DBE=130°，求∠DCE的度数；③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2、…、G9，若∠BDC=140°，∠BG1C=77°，求∠A的度数。(1)观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；解：(1)∠BDC=∠A+∠B+∠C，理由如下；如图，连接AD并延长至点F，由外角定理可得：∠BDF=∠B+∠BAD①，∠CDF=∠CAD+∠C②，①+②得：∠BDF+∠CDF=∠B+∠BAD+∠CAD+∠C，即∠BDC=∠B+∠A+∠C；(2)请你直接利用以上结论，解决以下三个问题：①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A=50°，直接写出∠ABX+∠ACX的结果；(2)①由(1)可知：∠ABX+∠A+∠ACX=∠BXC，∴∠ABX+50°+∠ACX=90°，∴∠ABX+∠ACX=40°；②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE=50°，∠DBE=130°，求∠DCE的度数；③如图4，∠ABD、∠ACD的10等分线相交于点G1、G2、…、G9，若∠BDC=140°，∠BG1C=77°，求∠A的度数。例8-3、如图，A、B分别是∠MON两边OM、ON上的动点（均不与点O重合）。(1)如图1，当∠MON=58°时，△AOB的外角∠NBA、∠MAB的平分线交于点C，求∠ACB的度数；(2)如图2，当∠MON=n°时，∠OAB，∠OBA的平分线交于点D，求∠ADB的度数（用含n的式子表示）；(3)如图3，当∠MON=α（α为定值，0°<α<90°）时，BE是∠NBA的平分线，BE的反向延长线与∠OAB的平分线交于点F。随着点A、B的运动，∠F的大小会改变吗？如果不会，求出∠F的度数（用含α的式子表示）；如果会，请说明理由。(1)如图1，当∠MON=58°时，△AOB的外角∠NBA、∠MAB的平分线交于点C，求∠ACB的度数；(2)如图2，当∠MON=n°时，∠OAB，∠OBA的平分线交于点D，求∠ADB的度数（用含n的式子表示）；(3)如图3，当∠MON=α（α为定值，0°<α<90°）时，BE是∠NBA的平分线，BE的反向延长线与∠OAB的平分线交于点F。随着点A、B的运动，∠F的大小会改变吗？如果不会，求出∠F的度数（用含α的式子表示）；如果会，请说明理由。例9-1、一个多边形的内角和是它的外角和的4倍，求：(1)这个多边形是几边形？(2)这个多边形共有多少条对角线？解：(1)设这个多边形是n边形，由题意可知：(n-2)·180°=4×360°，解得：n=10；例9-2、如图，七边形ABCDEFG中，EF、BA的延长线相交于点P，若∠ABC、∠BCD、∠CDE、∠DEF的外角的度数和为230°，求∠P的度数。解：如图，由题意可得：∠1+∠2+∠3+∠4=230°，∴∠5+∠6+∠7=360°-230°=130°，∵∠8=∠6+∠7，∴∠5+∠8=130°，∴∠P=180°-(∠5+∠8)=180°-130°=50°。章末复习