初中数学9.5 多项式的因式分解优质课件ppt

这是一份初中数学9.5 多项式的因式分解优质课件ppt，共28页。PPT课件主要包含了教学目标，公因式，最大公约数，ac2，x-1，因式分解与提公因式法，ma+mb+mc，x3+x2，abx-aby，整式乘法等内容，欢迎下载使用。

理解公因式的概念，掌握提取公因式的方法
理解因式分解的概念，明确因式分解与整式乘法的联系与区别
会用提公因式法进行因式分解
Q1：巧算：29×7+29×2.1+29×0.9。
【分析】原式=29×(7+2.1+0.9)=29×10=290
Q1：巧算：29×7+29×2.1+29×0.9
Q2：完成下列填空：(1) ma+mb+mc=( )(a+b+c) ；(2) x3+x2=( )(x+1) ；(3) abx-aby=( )(x-y) 。
【分析】(1)~(3)中提取的公因式分别为____，____，____。
m x2 ab
【公因式】多项式各项都含有的因式，称为这个多项式各项的公因式。
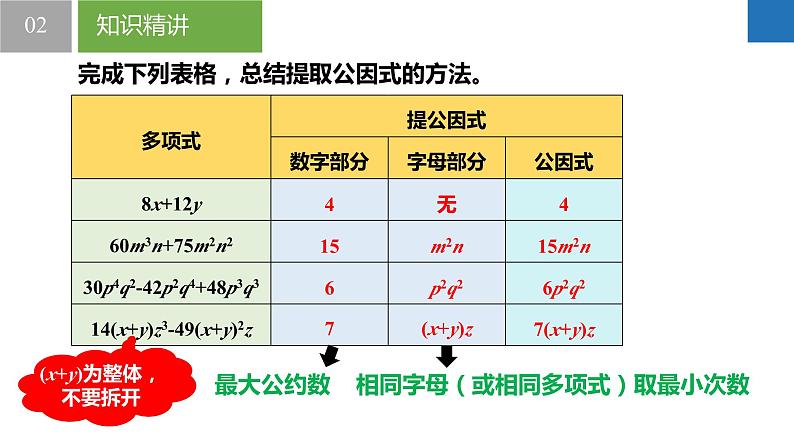
完成下列表格，总结提取公因式的方法。
(x+y)为整体，不要拆开
相同字母（或相同多项式）取最小次数
【提取公因式的方法】三“定”：①定系数，确定各项系数的最大公约数；②定字母，确定各项的相同字母（或相同多项式）因式；③定指数，确定各项相同字母（或相同多项式）因式的指数的最低次幂。
例1、多项式18abc2-12a2c6+8abc4的公因式是__________。
【分析】①定系数，最大公约数：2；②定字母，相同字母因式：a、c；③定指数，相同字母因式的指数的最低次幂：ac2。
例2、多项式a(x2-2x+1)与多项式(x-1)(x+1)的公因式是__________。
【分析】a(x2-2x+1)=a(x-1)2，
①定系数，最大公约数：1；②定字母，相同多项式因式：(x-1)；③定指数，相同字母因式的指数的最低次幂：(x-1)。
完成下列填空：(1) ma+mb+mc=( )(a+b+c) ，(2) x3+x2=( )(x+1) ，(3) abx-aby=( )(x-y) ，
(4) m(a+b+c)=____________； (5) x2(x+1)=____________ ； (6) ab(x-y)=____________。
【分析】(4)~(6)为________运算，运算的结果为______式；(1)~(3)的等号左侧为______式，右侧为______式之积，此运算为________。
【因式分解】把一个多项式写成几个整式的积的形式，叫做多项式的因式分解。
你能说出因式分解与整式乘法的联系与区别吗？
【总结】①联系：因式分解与整式乘法是互逆运算，因此因式分解可以用整式乘法来检验；
②区别：因式分解的结果是几个整式的积的形式，整式乘法的结果是多项式的形式。
ma+mb+mc=(m)(a+b+c) x3+x2=(x2)(x+1) abx-aby=(ab)(x-y)
【提公因式法】把多项式的公因式提到括号外，把多项式写成公因式与另一个多项式的积的形式，这种分解因式的方法叫做提公因式法。
因式分解+提公因式=提公因式法
分解因式：(1)-2x+4x2-6x3+8x4；
=-(2x·1-2x·2x+2x·3x2-2x·4x3)=-2x(1-2x+3x2-4x3)
【分析】(1)若多项式第一项是负的，一般要提出“-”号，使括号内的第一项的系数成为正数；提“-”号时，多项式的各项要变号，
原式=-(2x-4x2+6x3-8x4)
分解因式： (2)6a(m+2n)-4b(m+2n)；
(2)原式=2(m+2n)·3a-2(m+2n)·2b=2(m+2n)(3a-2b)
(m+2n)为整体，不要拆开
分解因式： (3)9(m+n)2-3(m-n)(m+n)。
(3)原式=3(m+n)·3(m+n)-3(m+n)·(m-n)=3(m+n)[3(m+n)-(m-n)]=3(m+n)(2m+4n)
=3(m+n)(2·m+2×2n)=6(m+n)(m+2n)
【注意点】①若多项式第一项是负的，一般要提出“-”号，使括号内的第一项的系数成为正数；提出“-”号时，多项式的各项要变号；②提的公因式有可能是单项式，也有可能是多项式，要有整体思想；③因式分解要彻底！！！
例1、式子从左到右的变形中，属于因式分解的是（　　）A．x2-1=x·x-1 B．x2+2xy+1=x(x+2y)+1C．a2b+ab3=ab(a+b2)D．x(x+y)=x2+xy
【分析】因式分解应是几个整式的积的形式。
例2、已知多项式2x2+bx+c分解因式为2(x-3)(x+1)，则b、c的值为（　　）A．b=3，c=-1B．b=-6，c=2C．b=-6，c=-4D．b=-4，c=-6
【分析】因式分解与整式乘法是互逆运算，因此因式分解可以用整式乘法来检验；
∵2x2+bx+c=2(x-3)(x+1)=2x2-4x-6，∴b=-4，c=-6。
例3、分解因式：(1)9x3y3-21x3y2+12x2y2； (2)y(2a-b)+x(b-2a)。
【分析】(1)原式=3x2y2·3xy-3x2y2·7x+3x2y2·4)=3x2y2(3xy-7x+4)
(2)原式=y·(2a-b)-x·(2a-b)=(2a-b)(y-x)
例4、分解因式：(1)(2x-y)(x+3y)-(2x+3y)(y-2x)；
【分析】(1)原式=(2x-y)·(x+3y)+(2x-y)·(2x+3y)=(2x-y)[(x+3y)+(2x+3y)]=(2x-y)(3x+6y)
=(2x-y)(3·x+3×2y)=3(2x-y)(x+2y)
例5、计算：(-5)2023+(-5)2024。
【分析】原式=1×(-5)2023+(-5)×(-5)2023=(1-5)×(-5)2023=-4×(-5)2023=4×52023。
例6、如图，某养鸡场老板准备用20米的篱笆围成一个边长为a、b的长方形场地，已知a2b+ab2=240，则这个长方形场地的面积为________平方米。
【分析】由题意可得：a+b=20÷2=10（米），这个长方形场地的面积为ab，∵a2b+ab2=240，∴ab(a+b)=240，解得：ab=24，∴这个长方形场地的面积为24平方米。
【公因式】多项式各项都含有的因式，称为这个多项式各项的公因式。【提取公因式的方法】三“定”：①定系数，确定各项系数的最大公约数；②定字母，确定各项的相同字母（或相同多项式）因式；③定指数，确定各项相同字母（或相同多项式）因式的指数的最低次幂。
【因式分解】把一个多项式写成几个整式的积的形式，叫做多项式的因式分解。【因式分解与整式乘法的联系与区别】①联系：因式分解与整式乘法是互逆运算，因此因式分解可以用整式乘法来检验；②区别：因式分解的结果是几个整式的积的形式，整式乘法的结果是多项式的形式。
【提公因式法】把多项式的公因式提到括号外，把多项式写成公因式与另一个多项式的积的形式，这种分解因式的方法叫做提公因式法。【注意点】①若多项式第一项是负的，一般要提出“-”号，使括号内的第一项的系数成为正数；提出“-”号时，多项式的各项要变号；②提的公因式有可能是单项式，也有可能是多项式，要有整体思想；③因式分解要彻底！！！