


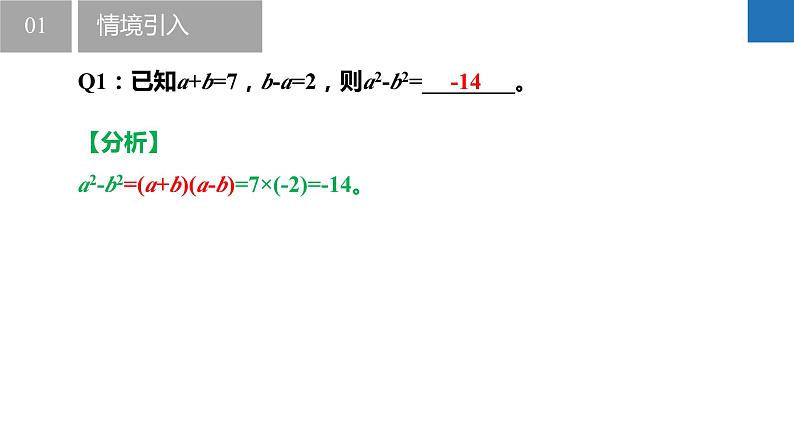




- 9.5.2多项式的因式分解-公式法(分层练习,5大题型)-2023-2024学年七年级数学下册同步精品课件+分层练习(苏科版) 课件 1 次下载
- 9.5.3多项式的因式分解-分组分解法(分层练习,3大题型)-2023-2024学年七年级数学下册同步精品课件+分层练习(苏科版) 课件 0 次下载
- 9.5.3多项式的因式分解-分组分解法(同步课件)-2023-2024学年七年级数学下册同步精品课件+分层练习(苏科版) 课件 0 次下载
- 9.5.4多项式的因式分解-二项式系数为1的十字相乘法(同步课件)-2023-2024学年七年级数学下册同步精品课件+分层练习(苏科版) 课件 0 次下载
- 9.5.4多项式的因式分解-十字相乘法(分层练习,4大题型)-2023-2024学年七年级数学下册同步精品课件+分层练习(苏科版) 课件 0 次下载
苏科版七年级下册9.5 多项式的因式分解优秀课件ppt
展开熟悉乘法公式的结构特征,能运用公式法进行因式分解
能在实数范围内分解因式
综合运用两个公式法因式分解;综合运用提公因式法与公式法因式分解,理解提公因式法的优先性
Q1:已知a+b=7,b-a=2,则a2-b2=________。
【分析】a2-b2=(a+b)(a-b)=7×(-2)=-14。
Q2:(1)a2-b2=(a+b)(a-b)与平方差公式有何关联?(2)a2-b2=(a+b)(a-b)是因式分解吗?
【分析】(1)a2-b2=(a+b)(a-b)即平方差公式的逆用;
(2)是,符合因式分解的定义:把一个多项式写成几个整式的积的形式,叫做多项式的因式分解。
【公式法——平方差公式】a2-b2=(a-b)(a+b)
请分析上述公式的结构特征:
【结构特征】公式的左边是两个数的平方差,右边是这两个数的和与这两个数的差的积。
【分析】(1)原式=(m+n)(m-n)
将2x、3y分别看作整体
(2)原式=(2x)2-(3y)2
=(2x+3y)(2x-3y)
分解因式:(4)x4-1;
(4)原式=(x2)2-12
=(x2+1)(x+1)(x-1)
=(x2+1)(x2-1)
分解因式:(5)(a+b+c)2-(a+b-c)2;
(5)原式=[a+b+c+(a+b-c) ][a+b+c+(a+b-c)]=(2a+2b)·2c
=2(a+b)·2c=4c(a+b)
分解因式:(6)49(x+y)2-16(x-y)2。
(6)原式=[7(x+y)]2-[4(x-y)]2=[7(x+y)+4(x-y)][7(x+y)-4(x-y)]=(11x+3y)(3x+11y)
【注意点】公式中的a和b可以是具体数,也可以是单项式或多项式。
议一议:x2-2能否分解因式?
【实数范围内分解因式】实数范围内分解因式是指可以把因式分解到实数的范围(可用无理数的形式来表示),一些式子在有理数的范围内无法分解因式,可是在实数范围内就可以继续分解因式。
PS:如无特别说明,因式分解的结果必须是每个因式在有理数范围内不能再分解为止。
分解因式(实数范围):(1)2x2-1; (2)a4-9。
例1、下列各式中,能用平方差公式分解因式的是( )A.x2+xy+y2B.4x2+4x-1C.9-3x+x2D.9x2-16y2
【分析】要用平方差公式分解因式,式子的结构应是两个数的平方差。
D.9x2-16y2=(3x)2-(4y)2=(3x+4y)(3x-4y)
【分析】(1)原式=52-(4x)2=(5+4x)(5-4x)
例2、分解因式:(1)25-16x2; (2)(4a+b)2-4(a+b)2。
(2)原式=(4a+b)2-(2a+2b)2=[4a+b+(2a+2b)][4a+b-(2a+2b)]=(6a+3b)(2a-b)=3(2a+b)(2a-b)
【分析】原式=(1034-34)(1034+34)=1000×1068=1068000
例3、巧算:10342-342。
例4、若x+y=2,则代数式x2-y2+4y的值等于_________。
【分析】x2-y2+4y=(x+y)(x-y)+4y=2(x-y)+4y=2x-2y+4y=2x+2y=2(x+y)=2×2=4。
例5、在实数范围内分解因式:x2y-19y。
Q1:(1)已知a+b=7,则a2+2ab+b2=________;(2)已知a-b=1,则a2-2ab+b2=________。
【分析】(1)a2+2ab+b2=(a+b)2=72=49;(2)a2-2ab+b2=(a-b)2=12=1。
Q2:(1)a2±2ab+b2=(a±b)2与完全平方公式有何关联?(2)a2±2ab+b2=(a±b)2是因式分解吗?
【分析】(1)a2±2ab+b2=(a±b)2即完全平方公式的逆用;
【公式法——完全平方公式】a2±2ab+b2=(a±b)2
【结构特征】公式的左边是两个数的平方和加上(或减去)这两个数乘积的2倍,右边是这两个数和(或差)的平方。
【运用公式法】运用平方差公式、完全平方公式,把一个多项式分解因式的方法叫做运用公式法。①a2-b2=(a+b)(a-b)②a2±2ab+b2=(a±b)2
【分析】(1)原式=a2-2·a·2+22=(a-2)2
分解因式:(3)4a2+4a+1; (4)4p2-20pq+25q2;
(3)原式=(2a)2+2×2a·1+12
(4)原式=(2p)2-2×2p·5q+(5q)2
分解因式:(5)4+12(x-y)+9(x-y)2。
(5)原式=22+2×2×3(x-y)+[3(x-y)]2
将3(x-y)看作整体
=[2+3(x-y)]2=(3x-3y+2)2
【分析】要用完全平方公式分解因式,式子的结构应是两个数的平方和加上(或减去)这两个数乘积的2倍。
【分析】(1)原式=x2y2-4xy+4=(xy)2-2·(xy)·2+22=(xy-2)2
例2、分解因式:(1)(xy-1)(xy-3)+1; (2)(a+b)2-12(a+b)+36。
(2)原式=(a+b)2-2·(a+b)·6+62=(a+b-6)2
例3、巧算:-101×190+1012+952。
【分析】原式=1012-2×101×95+952=(101-95)2=62=36。
例4、若4x2-kx+1能用完全平方公式分解因式,则k=( )A.-4 B.4 C.-4或4 D.-8或8
【分析】∵4x2-kx+1能用完全平方公式分解因式,∴4x2-4x+1=(2x-1)2或4x2+4x+1=(2x+1)2,∴k=4或-4。
公式法综合、提公因式法与公式法综合
【分析】(1)原式=(x2+4)2-(4x)2 =(x2+4x+4)(x2-4x+4)=(x+2)2(x-2)2
例1、综合运用两个公式分解因式:(1)(x2+4)2-16x2;
(2)原式=(a2-1)2-2·(a2-1)·3+32 =(a2-1-3)2 =(a2-4)2 =[(a+2)(a-2)]2=(a+2)2(a-2)2
例1、综合运用两个公式分解因式:(2)(a2-1)2+6(1-a2)+9;
(3)原式=(a+b)2-2(a+b)(a-b)+(a-b)2 =[(a+b)-(a-b)]2=(2b)2=4b2
例1、综合运用两个公式分解因式:(3)(a+b)2-2(a2-b2)+(a-b)2。
例2、综合运用提公因式法与公式法分解因式:(1)50a2-18b2; (2)a2(x-y)-4(x-y);
(1)原式=2(25a2-9b2)=2(5a+3b)(5a-3b)
(2)原式=(x-y)(a2-4)=(x-y)(a+2)(a-2)
例2、综合运用提公因式法与公式法分解因式:(3)3ax2+6axy+3ay2; (4)162x4-144x2y2+32y4。
(4)原式=2(81x4-72x2y2+16y4)=2(9x2-4y2)2=2[(3x+2y)(3x-2y)]2=2(3x+2y)2(3x-2y)2
(3)原式=3a(x2+2xy+y2)=3a(x+y)2
【因式分解的注意点】①通常,把一个多项式分解因式,应先提公因式,再运用公式,重点强调:因式分解的第一步永远都是提公因式;②进行多项式因式分解时,必须把每一个因式都分解到不能再分解为止。
【运用公式法】运用平方差公式、完全平方公式,把一个多项式分解因式的方法叫做运用公式法。①a2-b2=(a+b)(a-b)结构特征:公式的左边是两个数的平方差,右边是这两个数的和与这两个数的差的积。②a2±2ab+b2=(a±b)2结构特征:公式的左边是两个数的平方和加上(或减去)这两个数乘积的2倍,右边是这两个数和(或差)的平方。【注意点】公式中的a和b可以是具体数,也可以是单项式或多项式。
初中数学苏科版七年级下册9.5 多项式的因式分解获奖课件ppt: 这是一份初中数学苏科版七年级下册<a href="/sx/tb_c88675_t3/?tag_id=26" target="_blank">9.5 多项式的因式分解获奖课件ppt</a>,文件包含953多项式的因式分解-分组分解法三大题型原卷版docx、953多项式的因式分解-分组分解法三大题型解析版docx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
苏科版七年级下册9.5 多项式的因式分解精品课件ppt: 这是一份苏科版七年级下册<a href="/sx/tb_c88675_t3/?tag_id=26" target="_blank">9.5 多项式的因式分解精品课件ppt</a>,文件包含952多项式的因式分解-公式法五大题型原卷版docx、952多项式的因式分解-公式法五大题型解析版docx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
初中数学9.5 多项式的因式分解优质课件ppt: 这是一份初中数学<a href="/sx/tb_c88675_t3/?tag_id=26" target="_blank">9.5 多项式的因式分解优质课件ppt</a>,共28页。PPT课件主要包含了教学目标,公因式,最大公约数,ac2,x-1,因式分解与提公因式法,ma+mb+mc,x3+x2,abx-aby,整式乘法等内容,欢迎下载使用。













