2024海口中学高一下学期开学考试数学含解析

这是一份2024海口中学高一下学期开学考试数学含解析，共15页。试卷主要包含了 已知集合，则， 函数被称为狄利克雷函数，则， 函数的定义域为， 函数的大致图象是， 已知，则， 下列说法正确的是， 已知函数，则等内容，欢迎下载使用。
一､单选题（每小题5分）
1. 已知集合，则（ ）
A B.
C. D.
2. 函数被称为狄利克雷函数，则（ ）
A. 2B. C. 1D. 0
3. 函数的定义域为（ ）
A. B.
C D.
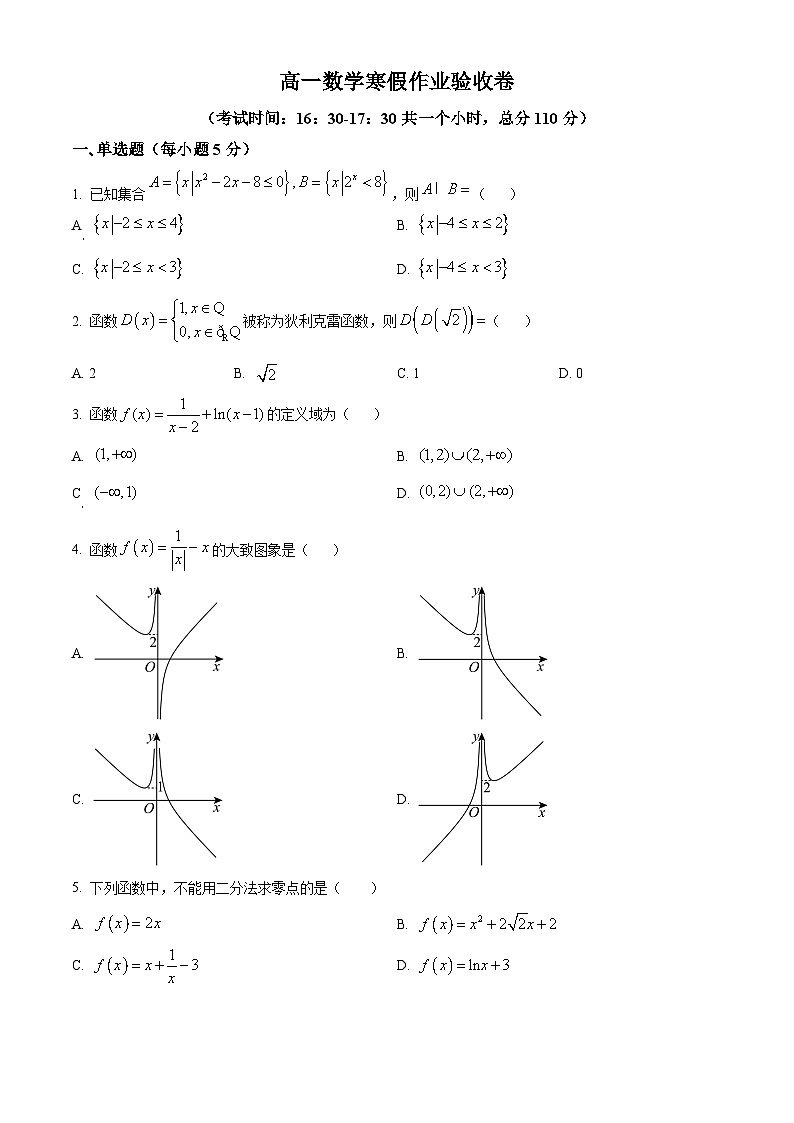
4. 函数的大致图象是（ ）
A. B.
C. D.
5. 下列函数中，不能用二分法求零点的是（ ）
A. B.
C. D.
6. 函数的定义域为，且对于任意均有成立，若，则正实数的取值范围为（ ）
A B.
C. D.
7. 已知，则（ ）
A. B. C. D.
8. 已知函数，若函数有四个不同零点，，，，且，则下列结论中正确的是（ ）
A. B.
C. D.
二､多选题（每小题6分）
9. 下列说法正确的是（ ）
A. “”是“”的必要不充分条件
B. “幂函数在上单调递减”的充要条件为“”
C. 命题的否定为：
D. 已知一扇形的圆心角，且其所在圆的半径，则扇形的弧长为
10. 已知函数，则（ ）
A. 的一个周期为2B. 的定义域是
C. 的图象关于点对称D. 在区间上单调递增
11. 已知关于的不等式的解集为，，，则（ ）
A.
B.
C. 的解集是
D. 的解集是或
三､填空题（每小题5分）
12. 已知，则__________.
13. 已知，且，则的最小值为________.
14. 已知函数在上有且仅有2个零点，则的取值范围为__________．
四､解答题
15. 已知函数．
（1）求函数的单调递增区间；
（2）将函数的图象向右平移个单位，再将所得图象上所有点的横坐标缩短为原来的倍，纵坐标不变，得到函数的图象，求函数在上的值域．
16. 已知函数奇函数．
（1）求实数的值；
（2）求关于的不等式的解集；
（3）设函数，若对任意的，总存在，使得成立，求实数的取值范围．
高一数学寒假作业验收卷
（考试时间：16：30-17：30共一个小时，总分110分）
一､单选题（每小题5分）
1. 已知集合，则（ ）
A. B.
C. D.
【答案】C
【解析】
分析】先求出集合中元素范围，再求交集即可.
【详解】，
，
则.
故选：C.
2. 函数被称为狄利克雷函数，则（ ）
A. 2B. C. 1D. 0
【答案】C
【解析】
【分析】利用定义结合分段函数性质计算即可.
【详解】由题意可知.
故选：C
3. 函数定义域为（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】由题可得，即可解出定义域.
【详解】因为，
所以要使函数有意义，
则，解得且，
所以的定义域为，
故选：B.
4. 函数的大致图象是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】利用单调性、最值结合图象可得答案.
【详解】当时，，减函数，排除AD；
当时，，
当且仅当时，取得最小值2，故排除C.
B选项的图象符合题意.
故选：B.
5. 下列函数中，不能用二分法求零点的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】利用二分法求零点的要求，逐一分析各选项即可得解.
【详解】不能用二分法求零点的函数，要么没有零点，要么零点两侧同号；
对于A，有唯一零点，且函数值在零点两侧异号，故可用二分法求零点；
对于B，有唯一零点，
但恒成立，故不可用二分法求零点；
对于C，有两个不同零点，且在每个零点左右两侧函数值异号，故可用二分法求零点；
对于D，有唯一零点，且函数值在零点两侧异号，故可用二分法求零点.
故选：B.
6. 函数的定义域为，且对于任意均有成立，若，则正实数的取值范围为（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】由题意，可知在上单调递减，又，所以,解不等式即可得解.
【详解】由题意,，不失一般性不妨假设，则，所以在上单调递减，
又，所以,
解不等式得,则正实数的取值范围为.
故选：B.
7. 已知，则（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据正弦的和差角公式展开可计算出，把转化成齐次式再运用弦化切的思想即可求解.
【详解】因为，所以，得，
显然，所以，而，
故选：B
8. 已知函数，若函数有四个不同的零点，，，，且，则下列结论中正确的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】由题意可得函数与有四个不同的交点，作出函数与的图象如图所示，然后结合图象逐个分析判断即可.
【详解】因为函数有四个不同的零点，
所以有四个不同的解，即函数与有四个不同的交点，
作出函数与的图象如图所示：
又时，，由图象可得，故B不正确，
由，得或，所以由图象可得，故A正确；
由图象可得，所以，即，
即，所以，故C错误；
又，关于对称，故，故D错误，
故选：A.
关键点点睛：此题考查对数函数图象的应用，考查函数与方程的综合应用，解题的关键是将问题转化为函数与有四个不同的交点，然后作出函数图象，结合图象分析判断，考查数形结合的思想，属于较难题.
二､多选题（每小题6分）
9. 下列说法正确的是（ ）
A. “”是“”的必要不充分条件
B. “幂函数在上单调递减”的充要条件为“”
C. 命题的否定为：
D. 已知一扇形的圆心角，且其所在圆的半径，则扇形的弧长为
【答案】AD
【解析】
【分析】由充分必要条件举例可得到A正确；由幂函数的单调性可得到B错误；由全称与特称命题的性质可得到C错误；由弧长公式可得到D正确.
【详解】A：，可以是，所以充分性不成立；若，则恒成立，所以必要性成立，故A正确；
B：由题意可知，又幂函数在上单调递减，则，故B错误；
C：命题的否定为：，故C错误；
D：扇形的圆心角，所以由弧长公式可知弧长为，故D正确.
故选：AD
10. 已知函数，则（ ）
A. 的一个周期为2B. 的定义域是
C. 的图象关于点对称D. 在区间上单调递增
【答案】ACD
【解析】
【分析】利用正切函数的图象与性质一一判定选项即可.
【详解】对于A，由可知其最小正周期，故A正确；
对于B，由可知，
故B错误；
对于C，由可知，
此时的图象关于点对称，故C正确；
对于D，由可知，
又上递增，显然，故D正确.
故选：ACD
11. 已知关于的不等式的解集为，，，则（ ）
A.
B.
C. 的解集是
D. 的解集是或
【答案】CD
【解析】
【分析】由题意可得1和5是方程的两根，且，利用韦达定理可得与的关系，然后逐项判断可得答案.
【详解】由题意可得和5是方程的两根，且，
由韦达定理可得，得，
对于A，因为，故A错误；
对于B，，故B错误；
对于C，不等式，即，即，得，
∴不等式的解集是，故C正确；
对于D，由不等式，得，即，
则，得或，即解集为或，故D正确.
故选：CD.
三､填空题（每小题5分）
12. 已知，则__________.
【答案】##
【解析】
【分析】根据三角函数的基本关系式，求得，再结合诱导公式，即可求解.
【详解】因为，所以，
又由.
故答案为：.
13. 已知，且，则的最小值为________.
【答案】##
【解析】
【分析】构造基本不等式“1”的代换，求出最小值.
【详解】因为，，
所以
当且仅当，即时等号成立.
所以的最小值为 .
故答案为：
14. 已知函数在上有且仅有2个零点，则的取值范围为__________．
【答案】
【解析】
【分析】首先求的取值范围，再根据余弦函数的图象，列式求的取值范围.
【详解】当时，．
因为在上有且仅有2个零点，所以，，解得．
故答案为：
四､解答题
15. 已知函数．
（1）求函数的单调递增区间；
（2）将函数的图象向右平移个单位，再将所得图象上所有点的横坐标缩短为原来的倍，纵坐标不变，得到函数的图象，求函数在上的值域．
【答案】（1）
（2）
【解析】
【分析】（1）由三角恒等变换化简的解析式，再利用单调性质求解；
（2）由图象变换得解析式，再利用整体法求值域.
【小问1详解】
因为，
令，得,
所以的单调递增区间为．
【小问2详解】
将函数的图象向右平移个单位，得到，
再将所得图象上所有点的横坐标缩短为原来的倍，纵坐标不变得到，
当，故，
所以值域为．
16. 已知函数为奇函数．
（1）求实数的值；
（2）求关于的不等式的解集；
（3）设函数，若对任意的，总存在，使得成立，求实数的取值范围．
【答案】（1）
（2）
（3）．
【解析】
【分析】（1）由奇函数定义计算即可得；
（2）可结合函数单调性计算，亦可借助换元法解不等式；
（3）计算出及的值域后，对任意的，总存在，使得成立即为的值域为的值域的子集，计算即可得.
【小问1详解】
因为函数为奇函数，所以，
即在定义域上恒成立，
整理得，故；
【小问2详解】
解法一：由（Ⅰ）知，
所以函数在和上单调递减，
且当时，，当时，，
所以，解得；
所以此时不等式的解集为；
解法二：因为，
令，则可化简为，
即，即，
解得，即．
所以此时不等式的解集为．
【小问3详解】
由（Ⅰ）得在的值域，
又，，
设，，则，
当时，取最小值为，当时，取最大值为，
即在上的值域，
又对任意的，总存在，使得成立，即，
所以，解得．