2023年河南省平顶山市中招第二次调研九年级数学模拟试题（原卷版+解析版）

这是一份2023年河南省平顶山市中招第二次调研九年级数学模拟试题（原卷版+解析版），文件包含精品解析2023年河南省平顶山市中招第二次调研九年级数学模拟试题原卷版docx、精品解析2023年河南省平顶山市中招第二次调研九年级数学模拟试题解析版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

1. 用正负数表示相反意义的量，在生活中有着广泛的应用．若零上记作，则零下可记作（ ）
A. B. C. D.
【答案】D
【解析】
【分析】此题考查了正负数的应用，根据正负数是表示一对意义相反的量进行辨别，解题的关键是能准确问题间的数量关系和具有意义相反的量．
【详解】解：∵零上记作，
∴零下记作，
故选：D．
2. 河南省文旅厅官方网站显示，2023年“五一”假期，郑汴洛等城市旅游出现“爆棚式”增长．全省接待游客达5518万人次，位居全国第一，旅游收入超300亿，位居全国前三名．将数据“5518万”用科学记数法表示为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】此题考查了科学记数法的表示方法，科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
【详解】解：．
故选：C．
3. 如图，将一个长方形纸条折成如图的形状，若，则的度数为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查平行线的性质，折叠的性质，由折叠的性质得到，由平角定义求出，由，得到，解题的关键是熟练掌握折叠的性质和平行线的性质．
【详解】解：如图，
由折叠的性质得到：，
∵，
∴，
∵，
∴．
故选：．
4. 下列运算正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】本题考查的是平方差公式、完全平方公式及整式的加减法则，根据平方差公式、完全平方公式及整式的加减法则对各选项进行逐一分析即可．
【详解】解：A、，原计算错误，不符合题意；
B、，原计算错误，不符合题意；
C、，原计算错误，不符合题意；
D、，原计算正确，符合题意．
故选：D．
5. 如图，方格纸上每个小正方形的边长都相同，若使阴影部分能折叠成一个正方体，则需剪掉一个小正方形，剪掉的小正方形不可以是（ ）

A. ①B. ②C. ③D. ④
【答案】D
【解析】
【分析】本题考查了正方体的展开图，根据正方体的11种展开图的模型即可求解．
【详解】解：由正方体展开图可知，剪掉的小正方形④不能折叠成正方体．
故选：D．
6. 为纪念五四青年节，某校举办了主题为“践行青年使命，谱写青春华章”的诗歌朗诵比赛，小明作为记录员，根据七位评委对某位选手所打的分数制作了如下的表格：
如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（ ）
A. 平均数B. 中位数C. 众数D. 方差
【答案】B
【解析】
【分析】本题考查了统计量的选择，根据中位数的定义：位于中间位置或中间两数的平均数，可以得到去掉一个最高分和一个最低分不影响中位数．
【详解】解：去掉一个最高分和一个最低分对中位数没有影响，
故选：B．
7. 若关于x的一元二次方程有实数根，则的取值范围是（ ）
A. B. 且C. D. 且
【答案】A
【解析】
【分析】本题考查一元二次方程根的判别式，根据方程有实数根，得到，列出不等式进行求解即可．
【详解】解：由题意得，，
解得：，
故选：A．
8. 下列选项中，菱形与正方形都具有的性质是（ ）
A. 四个角相等B. 两条对角线相等
C. 四条边相等D. 两条对角线把图形分成四个等腰直角三角形
【答案】C
【解析】
【分析】根据菱形和正方形的性质分别进行判断即可．
【详解】解：A、四个角相等不是菱形的性质，不符合题意；
B、两条对角线相等不是菱形的性质，不符合题意；
C、四条边相等既是菱形的性质，也是正方形的性质，符合题意；
D、两条对角线把图形分成四个等腰直角三角形不是菱形的性质，不符合题意．
故选：C．
【点睛】本题考查了菱形与正方形的性质，正方形是特殊的菱形，菱形拥有的性质正方形都拥有．
9. 如图，在中，已知，，点C为的中点，过点C作轴，垂足为D．将向右平移，当点C的对应点落在边上时，点D的对应点的坐标为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据等腰三角形和含的直角三角形的性质得点C和点D的坐标，作轴于点E，则，所以，所以，可知将是向右平移了2个单位长度，根据平移法则即可求出答案．
【详解】解：∵，，点C为的中点，
∴，
∵，
∴，
∴，
∴，
∴点C的坐标为，点D的坐标为，
将向右平移，当点C的对应点落在边上时，点D的对应点，
如图，作轴于点E，
∴，
∴，
∴，
∴将是向右平移了2个单位长度，
∴点D的对应点的坐标为．
故选：B．
【点睛】本题考查了坐标与图形变化﹣平移，等腰三角形的性质，勾股定理，解直角三角形，关键是掌握平移的性质．
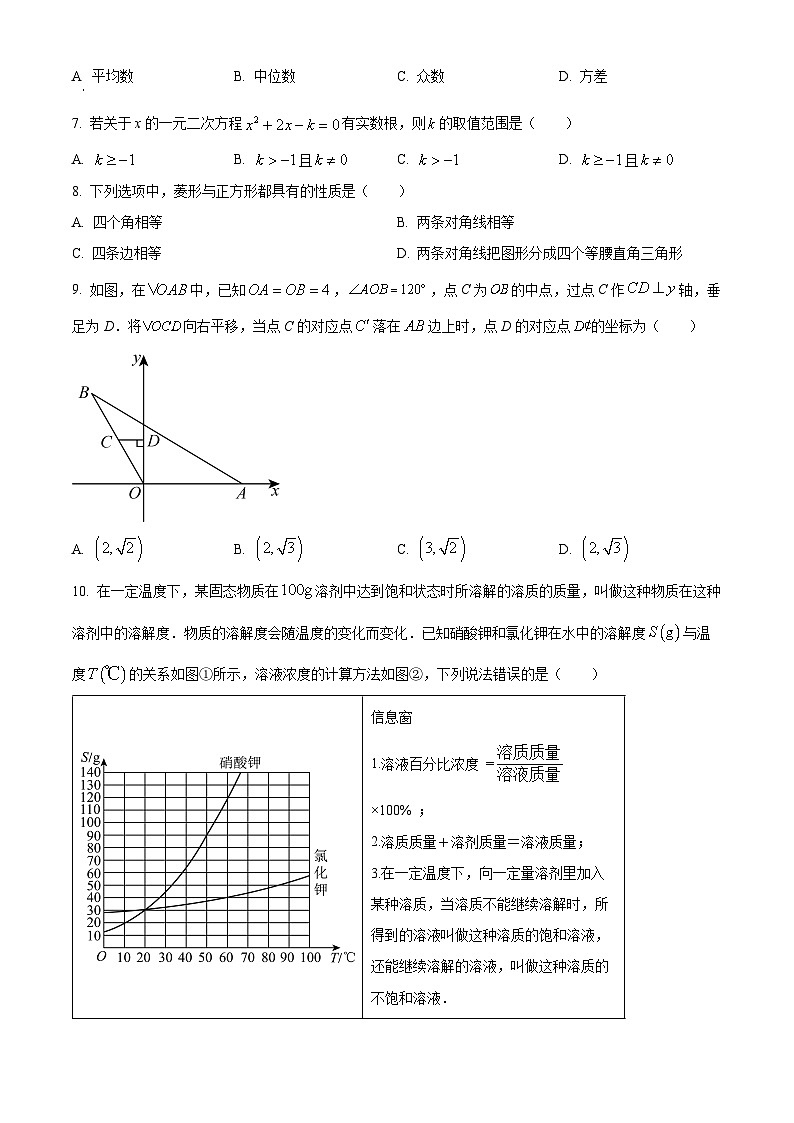
10. 在一定温度下，某固态物质在溶剂中达到饱和状态时所溶解的溶质的质量，叫做这种物质在这种溶剂中的溶解度．物质的溶解度会随温度的变化而变化．已知硝酸钾和氯化钾在水中的溶解度与温度的关系如图①所示，溶液浓度的计算方法如图②，下列说法错误的是（ ）
A. 硝酸钾的溶解度随温度变化的情况比氯化钾明显
B. 当时，硝酸钾的溶解度等于氯化钾的溶解度
C. 当时，硝酸钾加入水中得到的溶液浓度为
D. 当时，氯化钾加入水中得到的是饱和氯化钾溶液
【答案】C
【解析】
【分析】本题主要考查了函数的图象，根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件是解题的关键．根据函数图象横纵坐标表示的意义判断即可．
详解】解：由图象可知：
A．硝酸钾的溶解度随温度变化的情况比氯化钾明显，故选项A说法正确，不符合题意；
B．当时，硝酸钾的溶解度等于氯化钾的溶解度，故选项B说法正确，不符合题意；
C．当时，硝酸钾加入水中得到的溶液浓度为，故选项C说法错，符合题意；
D．当时，氯化钾加入水中得到的是饱和氯化钾溶液，故选项D说法正确，不符合题意．
故选：C．
二、填空题（每小题3分，共15分）
11. 请写出一个绝对值大于1负无理数 __．
【答案】（答案不唯一）
【解析】
【分析】此题考查了无理数，实数绝对值的应用和大小比较的，关键是能准确理解并运用该知识．运用实数的绝对值知识和大小比较方法进行求解．
【详解】解：，
故答案为：（答案不唯一）．
12. 不等式组的解集是______．
【答案】
【解析】
【分析】本题考查求不等式组的解集，分别求出每一个不等式的解集，找到它们的公共部分，即可，正确的求出每一个不等式的解集，是解题的关键．
【详解】解：
∵解不等式①得：，
解不等式②得：，
∴不等式组的解集是，
故答案为：．
13. 不透明的布袋中有红､黄､蓝3种只是颜色不同的钢笔各1支，先从中摸出1支，记录下它的颜色，将它放回布袋并搅匀，再从中随机摸出1支，记录下颜色，那么这两次摸出的钢笔为红色､黄色各一支的概率为_________．
【答案】
【解析】
【分析】先画出树状图，从而可得这两次摸出的钢笔的所有可能的结果，再找出这两次摸出的钢笔为红色､黄色各一支的结果，然后利用概率公式即可得．
【详解】解：将红､黄､蓝3种只是颜色不同的钢笔分别记为、、，
由题意，画出树状图如下：
由图可知，这两次摸出的钢笔的所有可能的结果共有9种，它们每一种出现的可能性都相等；其中，这两次摸出的钢笔为红色､黄色各一支的结果有2种，
则所求的概率为，
故答案为：．
【点睛】本题考查了利用列举法求概率，正确画出树状图是解题关键．
14. 如图，湖旁边有一建筑物，某数学兴趣小组决定测量它的高度．他们首先在点处测得建筑物最高点的仰角为，然后沿方向前进12米到达处，又测得点的仰角为．请你帮助该小组同学，计算建筑物的高度约为___________米．（结果精确到1米，参考数据）

【答案】16
【解析】
【分析】本题考查了解直角三角形的应用仰角俯角问题，根据题意可得：，米，然后设米，则米，在中，利用锐角三角函数的定义求出的长，再在中，利用锐角三角函数的定义求出的长，从而列出关于的方程，进行计算即可解答，熟练掌握锐角三角函数的定义是解题的关键．
【详解】解：由题意得：，米，
设米，
米，
在中，，
米，
在中，，
（米，
，
解得：，
（米，
建筑物的高度约为16米，
故答案为：16．
15. 如图，在矩形中，点为边上一点，且，，连接，将绕点逆时针旋转，当点的对应点落在直线上时，点的运动路径的长为 __．（结果保留π）
【答案】或
【解析】
【分析】本题考查了矩形的性质、弧长的计算以及旋转的性质，解答本题的关键是分类讨论，在中，由勾股定理得到：，再由题意分类讨论：当点落在线段上时、当点落在线段的延长线上时，分别求出的长即可．
【详解】解：矩形中，，
在中，，，
，
将绕点逆时针旋转得到，当点落在线段上时，，
，
的长为；
当点落在线段的延长线上时，
则，
，
的长为，
综上所述，的长为或．
故答案为：或．
三、解答题（本大题共8小题，满分75分）
16. （1）计算：．
（2）化简：．
【答案】（1）0（2）
【解析】
【分析】本题考查了分式的混合运算，实数的运算，负整数指数幂，零指数幂，准确熟练地进行计算是解题的关键．
（1）先化简各式，然后再进行计算即可解答；
（2）先利用异分母分式加减法法则计算括号里，再算括号外，即可解答．
【详解】解：（1）原式
；
（2）原式
．
17. 某地政府为了旅游宣传，决定从甲、乙两家民宿中推选一家为“最美民宿”进行线上推广．现从两家的顾客中各随机抽取20名，进行满意度调查打分（满分10分，只打整数分），并对分数整理、描述和分析，下面给出了部分信息．
（ⅰ）甲民宿20名顾客的满意度分数为：10，5，8，7，10，8，9，8，10，7，9，7，9，7，6，8，9，6，5，9
（ⅱ）甲、乙两家民宿的满意度分数的平均数、众数、中位数、9分及9分以上人数所占百分比如下表所示：
（ⅲ）乙民宿20名顾客的满意度分数条形统计图如图：
​
根据以上信息，解答下列问题：
（1）直接写出上述表中的a，b，c的值；
（2）五一假期期间，共有100人入住甲民宿，80人入住乙民宿，估计入住两家民宿的顾客能打9分及9分以上的人数共有多少人？
（3）根据以上信息，你会选择哪一家为“最美民宿”？请说明理由．（写出两条理由即可）
【答案】17. ，，
18. 64人 19. 甲民宿，理由：甲民宿顾客满意度分数的平均数、中位数都比乙民宿顾客满意度分数的平均数、中位数要大，因此选择甲民宿
【解析】
【分析】本题考查条形统计图，平均数、中位数、众数以及样本估计总体，理解平均数、中位数、众数的定义，掌握平均数、中位数、众数的计算方法是解决问题的关键．
（1）根据中位数、众数的定义进行计算即可；
（2）分别求出样本中，入住甲民宿、乙民宿的顾客打9分及9分以上的人数所占的百分比，估计总体中入住甲民宿、乙民宿的顾客打9分及9分以上的人数所占的百分比，由频率，进行计算即可；
（3）根据平均数、中位数的大小比较得出答案．
【小问1详解】
解：将样本中，甲民宿顾客满意度分数出现次数最多的是9分，共出现5次，因此甲民宿顾客满意度分数的众数是9分，即，
将样本中20名顾客对乙民宿满意度分数从小到大排列后，处在中间位置的两个数的平均数为，因此中位数是8分，即，
乙民宿顾客满意度分数在9分及9分以上人数所占百分比为，即，
答：，，；
【小问2详解】
（人），
答：入住两家民宿的顾客能打9分及9分以上的人数大约有64人；
【小问3详解】
甲民宿，理由：甲民宿顾客满意度分数的平均数、中位数都比乙民宿顾客满意度分数的平均数、中位数要大，因此选择甲民宿．
18. 如图，已知一次函数与轴交于点，与反比例函数的图象交于点．
（1）求一次函数和反比例函数的解析式；
（2）点P为x轴上一动点，且的值最小．
①画出点P的位置，并直接写出点P的坐标；
②求出此时的面积．
【答案】（1），
（2）①，图见解析；②1
【解析】
【分析】本题是反比例函数与一次函数的交点问题，考查了待定系数法求函数的解析式，轴对称最短路线问题，三角形的面积，熟练掌握待定系数法是解题的关键．
（1）利用待定系数法即可求解；
（2）①求得点的坐标，作出点关于轴的对称点，连接，与轴的交点即为点，此时的值最小，为线段的长度；②利用轴对称的性质，利用即可求得．
【小问1详解】
解：一次函数 与轴交于点，与反比例函数 的图象交于点，
，，
，，
一次函数为，反比例函数为；
【小问2详解】
解：①令，则，
，
点关于轴的对称点，连接如图，点即为所求，
设直线为，
代入点得，，
解得，
直线为，
令，则，
解得，
；
②，
．
19. 阅读材料：北师大版七年级下册教材24页为大家介绍了杨辉三角．
（1）应用规律：
①直接写出的展开式， ；
②的展开式中共有 项，所有项的系数和为 ；
（2）代数推理：
已知m为整数，求证：能被18整除．
【答案】（1）①；②7，64
（2）见解析
【解析】
【分析】本题考查了数字规律，多项式乘法，因式分解的应用，找出本题的数字规律是正确解题的关键．
（1）直接利用已知式子中系数变化规律进而得出答案；
（2）直接利用已知式子中系数变化规律进而得出答案．
【小问1详解】
解：根据规律得：
①；
②，
的展开式中共有7项，所有项的系数和为；
故答案为：，7，64；
【小问2详解】
证明：，
，
能被18整除．
20. 某中学为弘扬中国传统文化，深度开展“读名著，诵经典”活动，计划采购A，B两类图书．通过市场调研，每套A种图书的价格是每套B种图书价格的1.5倍，用2400元购买的B种图书比用3000元购买的A种图书多5套．
（1）A，B两种图书每套价格分别为多少元？
（2）现学校计划采购A，B两类图书共90套，且A种图书数量不低于B种图书数量的一半，请你用函数的知识说明，如何采购能使总费用最低？并求出最低费用．
【答案】（1）A种图书每套120元，B种图书每套800元
（2）学校购买A种图书30套，则购买B种图书60套时，总费用最低，最低费用为8400元
【解析】
【分析】本题考查一次函数的应用，分式方程的应用，一元一次不等式的应用，关键是找到数量关系列出函数解析式或方程和不等式．
（1）设B种图书每套x元，则A种图书每套元，根据用2400元购买的B种图书比用3000元购买的A种图书多5套列出方程，解方程即可，注意验根；
（2）设学校购买A种图书a套，则购买B种图书套，购买图书的总费用为y元，根据总费用两种图书费用之和列出函数解析式，再根据A种图书数量不低于B种图书数量的一半求出a的取值范围，由函数的性质求最值．
【小问1详解】
解：设B种图书每套x元，则A种图书每套1.5x元，
根据题意得：，
解得，
经检验，是原方程的解，
此时，
答：A种图书每套120元，B种图书每套800元；
【小问2详解】
解：设学校购买A种图书a套，购买B种图书套，购买图书的总费用y元，
由题意得：，
∵，
∴y随x的增大而增大，
∵A种图书数量不低于B种图书数量的一半，
∴，
解得，
∴当时，y最小，最小值为8400，
此时（套），
答：学校购买A种图书30套，则购买B种图书60套时，总费用最低，最低费用为8400元．
21. 如图，在平面直角坐标系中，抛物线的图象交轴于，两点，交轴于点，已知点坐标为，且，连接．
（1）求抛物线的解析式，并直接写出其顶点的坐标；
（2）将线段向右水平移动m个单位长度，若它与抛物线有交点，求出m的取值范围．
【答案】（1），
（2）
【解析】
【分析】本题考查了二次函数的图象与性质，图象的交点问题，关键是让线段运动起来，找到临界值．
（1）由点坐标和，求抛物线的解析式，用配方法求顶点的坐标；
（2）找到与抛物线有交点时的临界值，一个是平移后的纵坐标为，一个是与重合．
【小问1详解】
解：把点坐标代入抛物线，得，
，
，
抛物线的解析式为，
，
顶点的坐标为；
小问2详解】
解：当时，
，
令，
，，
令，
，，
，
，
．
22. 提出问题：古希腊数学家欧几里得（约公元前325——公元前265），被称为“几何学之父”．在其所著的《几何原本》中，包含了5条公理、5条公设、23个定义和467个命题，即先提出公理、公设和定义，再由简到繁予以证明，并在此基础上形成了欧式几何学体系．《几何原本》第3卷给出其中一个命题：如果圆外的一点向圆引两条直线，一条与圆相切，一条穿过圆，那么被圆截得的线段与该点到凸圆之间的线段为边构成的矩形的面积等于以该点向圆引的切线所构成的正方形的面积．如图1，上述结论可表示为，你能说明其中的道理吗？
探索问题：小明在探究的过程中发现，线段的位置有两种情况，即过圆心和不过圆心．
如图2，当经过圆心时，小明同学进行了如下推理：连接，易得，又，所以，可得对应边成比例，进而可知，当经过圆心时，得．当不经过圆心时，请补全下列推理过程．
（1）已知：如图3，为的切线，为切点，与相交于，两点，连接，．求证：．
证明： ．
（2）解决问题：如图4，已知为的直径，为延长线上一点，切于点，连接，若，，请直接写出的长．
【答案】（1）见解析 （2）
【解析】
【分析】（1）连接并延长，交于点，连接，由圆周角定理可得，根据三角形内角和定理得，由切线的性质得，即，进而可得，再根据圆周角定理可得，于是得到，以此可证明，利用相似三角形的性质即可得到证明；
（2）连接、，易证明，利用相似三角形的性质可得，进而得到，，于是得，设，则，在中，利用勾股定理建立方程求出的值，进而求出的长．
【小问1详解】
证明：如图，连接并延长，交于点，连接，
为的直径，
，
，
为的切线，为切点，
，即，
，
，
，
，
又，
，
，
；
【小问2详解】
解：如图，连接、，
为的直径，
，即，
为的切线，
，即，
，
，
，
又，
，
，即，
，，
，
设，则，
在中，，
，
解得：，（不合题意，舍去），
．
【点睛】本题主要考查切线的性质、圆周角定理、相似三角形的判定与性质、等腰三角形的性质、勾股定理，解题关键是根据题干所给条件，证明三角形相似，利用相似三角形的性质解决问题．
23. 在边长为2的正方形中，点是射线上一动点（点不与，重合），与相交于点，射线与射线相交于点，是的中点，连接，．
（1）如图1，当点在中点时，判断：与的位置关系为 ；
（2）如图2，当点在的延长线上时，（1）中的结论是否仍然成立？请给出证明；
（3）在点E运动过程中，当是等腰三角形时，直接写出的长．
【答案】（1）
（2）成立，证明见解析
（3）或
【解析】
【分析】（1）由正方形的性质得出，，由证明，由全等三角形的性质得出，由直角三角形斜边上的中线性质得出，证出，由平行线的性质得出，因此，得出，即可得出结论；
（2）同（1），即可得出结论；
（3）分两种情况：①当点在边上时，由，要使是等腰三角形，必须，得出，由三角形的外角性质得出，由直角三角形的性质得出，得出；②当点在的延长线上时，同①方法可得；即可得出结论．
【小问1详解】
解：，理由如下：
四边形是正方形，
，，
，
，
，
，是的中点，
，
，
，
，
，
，
，
故答案为：；
【小问2详解】
成立；理由如下：
四边形是正方形，
，，
，
，
，
，是的中点，
，
，
，
，
，
，
；
【小问3详解】
解：分两种情况：①当点在边上时，
，要使是等腰三角形，必须，
，
，
，
，
；
②当点在的延长线上时，
，要使是等腰三角形，必须，
，
，
，
，
，
，
综上所述，当是等腰三角形时，或．
【点睛】本题是四边形综合题，考查了正方形的性质、全等三角形的判定与性质、直角三角形斜边上的中线性质、等腰三角形的性质、直角三角形的性质、含角的直角三角形的性质等知识；本题综合性强，有一定难度，证明三角形全等是解决问题的关键．
平均数
中位数
众数
方差

信息窗
1.溶液百分比浓度 =×100% ；
2.溶质质量＋溶剂质量＝溶液质量；
3.在一定温度下，向一定量溶剂里加入某种溶质，当溶质不能继续溶解时，所得到的溶液叫做这种溶质的饱和溶液，还能继续溶解的溶液，叫做这种溶质的不饱和溶液．
图①
图②
民宿
平均分
众数
中位数
9分及9分以上人数
甲
7.85
a
8
乙
7.75
8
b
c
杨辉三角
如果将为非负整数）的展开式的每一项按字母的次数由大到小排列，就可以得到下面的等式：
，它只有一项，系数为1；
，它有两项，系数分别为1，1；
，它有三项，系数分别为1，2，1；
，它有四项，系数分别为1，3，3，1；
将上述每个式子的各项系数排成该表．
观察该表，可以发现每一行首末都是1，并且下一行的数比上一行多1个，中间各数都写在上一行两数的中间，且等于它们的和．按照这个规律可以将这个表继续往下写．
该表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过，而他是摘录自北宋时期数学家贾宪著的《开方作法本源》中的“开方作法本源图”，因而人们把这个表叫做杨辉三角或贾宪三角，在欧洲这个表叫做帕斯卡三角形．帕斯卡（B．Pascal，1623——1662）是1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年．