


2024年中考数学复习课件---第7讲 一元一次不等式(组)及其应用
展开1. 结合具体问题,了解不等式的意义,探索不等式的基本性质.2. 能解数字系数的一元一次不等式,并能在数轴上表示出解集;会用数 轴确定两个一元一次不等式组成的不等式组的解集.3. 能根据具体问题中的数量关系,列出一元一次不等式,解决简单的问 题.
教材链接人教:七下P113~P133 北师:八下P36~P63 湘教:八上P129~P153
一元一次不等式(组)及其应用
一元一次不等式(组)的解法及解集表示
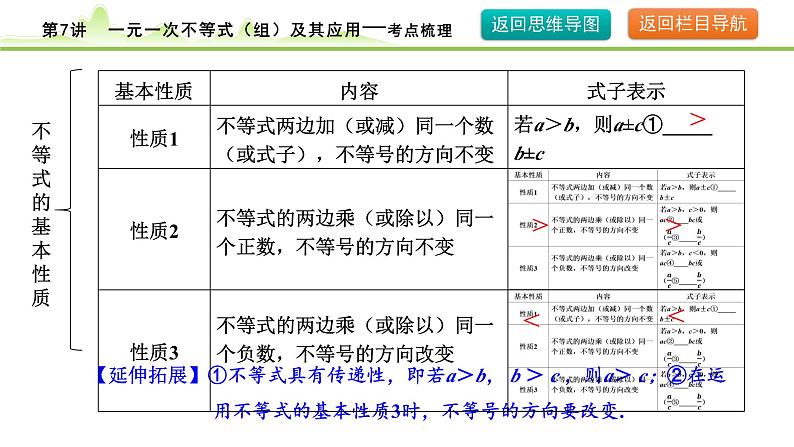
【延伸拓展】①不等式具有传递性,即若a>b, b > c ,则a> c;②在运 用不等式的基本性质3时,不等号的方向要改变.
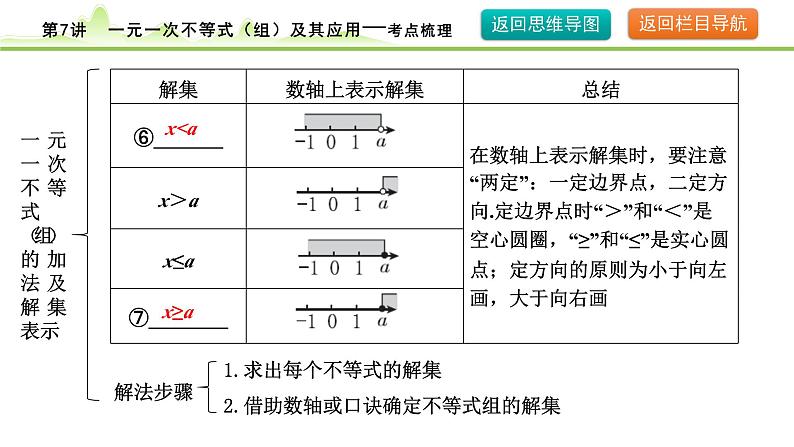
一元一次不等式(组)的加法及解集表示
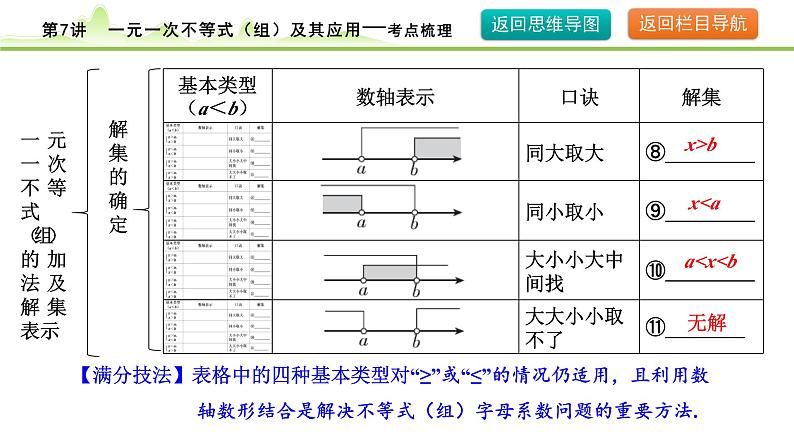
1.求出每个不等式的解集2.借助数轴或口诀确定不等式组的解集
【满分技法】表格中的四种基本类型对“≥”或“≤”的情况仍适用,且利用数 轴数形结合是解决不等式(组)字母系数问题的重要方法.
一元一次不等式(组)的实际应用
与列方程解应用题类似,即:(1)审题;(2)设未知数;(3)列出不等式;(4)解不等式;(5)写出答案,并检验是否符合题意
列不等式解应用题常与方案设计型问题相联系,如最大利润、最优方案等;一般题干中含有“至少(≥)”“最多(≤)”“不低于( ≥ )”“不超过( ≤ )”“不大于( ≤ )”“不小于( ≥ )”等词,解题的关键是将这些词转化为正确的数学符号
根据不等式(组)的解集确定字母的取值范围
一元一次不等式(组)的应用
例2 (2022·贵阳观山湖区模拟)“广汉三星堆”由于有新的文物出土, 景区管委会为了方便更多的参观者在园区内参观与休息,决定向 某公司采购一批户外休闲椅.经过了解该公司出售弧形椅和条形 椅两种类型的休闲椅,已知条形椅的单价是弧形椅的单价的0.5倍, 用4 800元购买弧形椅的数量比用3 200元购买条形椅的数量少10 张.
(1)弧形椅和条形椅的单价分别是多少元?
(2)已知一张弧形椅可坐5人,一张条形椅可坐3人,景区计划共购进300张休闲椅,并保证至少增加1 100个座位.请问:应如何安排购买方案最节省费用?最低费用是多少元?
解:(2)设购进弧形椅m张,则购进条形椅(300-m)张,由题意,得 5m+3(300-m)≥1 100,解得m≥100. 设购买休闲椅所需的费用为W元,则W=160m+80(300-m)=80m+24 000. ∵80>0,∴W随m的增大而增大. ∴当m=100时,W有最小值,W最小=80×100+24 000=32 000(元). 300-m=300-100=200(张). 答:购进100张弧形椅,200张条形椅最节省费用,最低费用是32 000元.
方法指导1.设未知数时,不能设“至少”“最多”,而要设“是多少”.2.列不等式解应用题时,要注意描述数量关系的词语与不等号的对应关系.3.最后要根据实际情况选取符合实际的解作答,如人数是正整数,时间不能为负数等.
4. (2022·遵义红花岗区二模)如图为小丽和小欧依序进入电梯时,因 超重而警示音响起的过程,且过程中没有其他人进出.该电梯载重超 过480公斤时警示音响起.已知小丽为45公斤,小欧为65公斤.若小丽 进入电梯前,电梯内已载重x公斤,则所有满足题意的x可用下列哪一 个不等式表示( ) A.415
(1)如果只在某一家超市购买所需球拍和乒乓球,那么去A超市还是B超市买更合算?
解:(1)由题意,得去A超市购买n副球拍和kn个乒乓球的费用为0.9(20n+kn) 元,去B超市购买n副球拍和kn个乒乓球的费用为[20n+n(k-3)]元, 由0.9(20n+kn)<20n+n(k-3),解得k>10; 由0.9(20n+kn)=20n+n(k-3),解得k=10; 由0.9(20n+kn)>20n+n(k-3),解得k<10. ∴当k>10时,去A超市购买更合算;当k=10时,去A,B两家超市购买都一 样;当3≤k<10时,去B超市购买更合算.
(2)当k=12时,请设计最省钱的购买方案.
解:(2)当k=12时,购买n副球拍应配12n个乒乓球 . 若只在A超市购买,则费用为0.9(20n+12n)=28.8n(元); 若只在B超市购买,则费用为20n+(12-3)n=29n(元); 若在B超市购买n副球拍,然后在A超市购买不足的乒乓球,则费 用为20n+0.9×(12-3)n=28.1n(元). 显然28.1n<28.8n<29n, ∴最省钱的购买方案为在B超市购买n副球拍同时获得送的3n 个乒乓球,然后在A超市按九折购买9n个乒乓球.
(2017~2022)
(贵阳6年4考,遵义6年3考,毕节6年5考)
5.[2021·贵阳17(1)题6分]有三个不等式2x+3<-1,-5x>15,3(x-1)>6,请在 其中任选两个不等式,组成一个不等式组,并求出它的解集.
(贵阳6年3考,遵义6年5考)
8.(2021·遵义5题4分)小明用30元购买铅笔和签字笔,已知铅笔和签字 笔的单价分别是2元和5元,他买了2支铅笔后,最多还能买几支签字笔? 设小明还能买x支签字笔,则下列不等关系正确的是( ) A.5×2+2x≥30 B.5×2+2x≤30 C.2×2+5x≥30 D.2×2+5x≤30
9.(2019·贵阳20题10分)某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元.
(1)求A,B两款毕业纪念册的销售单价;
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能购买多少本A款毕业纪念册.
解:(2)设能购买a本A款毕业纪念册,则购买(60-a)本B款毕业纪念册, 根据题意,可得10a+8(60-a)≤529, 解得a≤24.5, 则最多能够买24本A款毕业纪念册.
10.(2022·黔西南州24题12分)某乡镇新打造的“田园风光”景区今年 计划改造一片绿化地,种植A,B两种花卉,已知3盆A种花卉和4盆B种 花卉的种植费用为330元,4盆A种花卉和3盆B种花卉的种植费用为 300元.
(1)每盆A种花卉和每盆B种花卉的种植费用各是多少元?
第7讲 一元一次不等式(组)及其应用课件---2024年中考数学一轮复习: 这是一份第7讲 一元一次不等式(组)及其应用课件---2024年中考数学一轮复习,共21页。PPT课件主要包含了综合模拟练,基础全练,m≤2,x≥-1,x≤2,-1≤x≤2,挑战高分,a≥2,x-2,x≤3等内容,欢迎下载使用。
第7讲 一元一次不等式(组)及其应用课件---2024年中考数学一轮复习: 这是一份第7讲 一元一次不等式(组)及其应用课件---2024年中考数学一轮复习,共37页。PPT课件主要包含了栏目导航,不等式的基本性质,一元一次不等式及解法,不等式的解,不等式的解集,去括号,合并同类项,b<x<a,题型1,核心素养·推理能力等内容,欢迎下载使用。
2023年河北省中考数学复习全方位第7讲 一元一次不等式组及其应用 课件: 这是一份2023年河北省中考数学复习全方位第7讲 一元一次不等式组及其应用 课件,共42页。PPT课件主要包含了真题演练,解1-2,2m-1,考点梳理,去括号,合并同类项,bxa,题型突破,去分母时漏乘常数项,a≥2等内容,欢迎下载使用。












