





2024年中考数学复习课件---第12讲 二次函数的图象与性质
展开1.能画二次函数的图象,通过图象了解二次函数的性质,知道二次函数 系数与图象形状和对称轴的关系.2.会求二次函数的最大值或最小值,并能确定相应自变量的值.3.知道二次函数和一元二次方程之间的关系,会利用二次函数的图象求 一元二次方程的近似解.
教材链接人教:九上P27~P48 北师:九下P28~P45、P51~P57 湘教:九下P1~P24
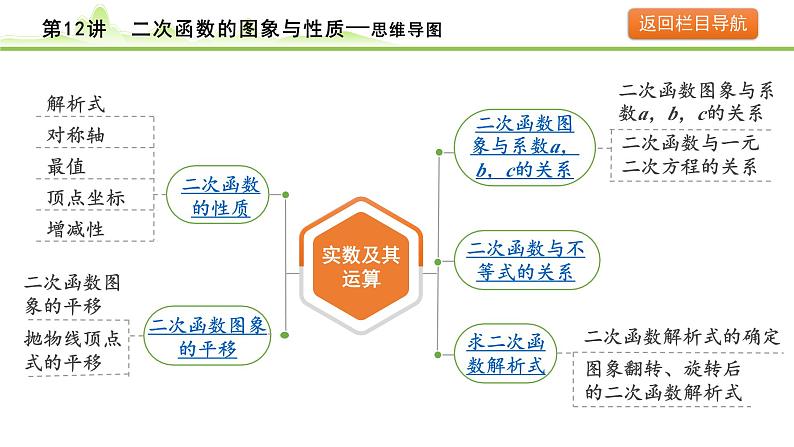
二次函数图象与系数a,b,c的关系
二次函数与一元二次方程的关系
图象翻转、旋转后的二次函数解析式
【满分技法】两点在对称轴异侧,当a>0时,点与对称轴距离越远,y值越大; 当a<0时,点与对称轴距离越近,y值越大.
向左平移m(m>0)个单位:y=a(x⑪______)2 +b(x ⑫_____)+c
1.二次函数图象的平移
向右平移m(m>0)个单位:y=a(x⑬______)2 +b(x ⑭____)+c
2.抛物线顶点式的平移
【易错提示】点坐标的平移规律是“左加右减,上加下减”,函数图象的平移规 律是“左加右减,上加下减”,不要弄混.
二次函数的图象与系数a,b,c的关系
二次函数与不等式的关系
2.图象翻折、旋转后的二次函数解析式
例1 如图,二次函数y=ax2+bx+c(a≠0)的图象对称轴为直线x=-1,与x轴的 一个交点B的坐标为(1,0),下列结论:
方法指导2.根据二次函数图象及对称轴确定增减性①在对称轴同侧:比较纵坐标;②在对称轴异侧:利用对称关系转换为同侧或根据离对称轴的远近判断.
例2 已知二次函数y=x2+bx+c的图象与y轴交于点A(0,-6),与x轴的一个交 点坐标是B(-2,0). (1)求二次函数的关系式,并写出顶点坐标;
3.(2022·黔东南州一模)抛物线y=x2-x-1关于坐标原点对称的抛物线的 解析式为 .
4.(2022·铜仁一模)已知抛物线y=x2+bx+c过A(c,12),B(■,■)两点,且交 于y轴的负半轴.请证明抛物线的对称轴是直线x=1(其中点B的坐标被 污渍盖住了).
(1)请问:能否根据题中信息求抛物线的解析式?若能,请写出解题过程; 若不能,请说明理由.
∴c2-c-12=0.解得c1=4,c2=-3.∵抛物线交于y轴的负半轴, ∴c<0.∴c=-3.∴抛物线的解析式为y=x2-2x-3.
(2)请把原题补充完整,并完成原题证明.
二次函数与方程、不等式的关系
例3 (2022·贵阳南明区模拟)已知二次 函数y=ax2+bx+c(a≠0)的图象经 A(-2,1),B(2,-3)两点.
(1)求分别以A(-2,1),B(2,-3)两点为顶点的二次函数表达式;
(2)求b的值,判断此二次函数图象与x轴的交点情况,并说明理由;
(3)设(m,0)是该函数图象与x轴的一个公共点.当-3
7.(2022·黔西南州兴义市模拟)抛物线y=ax2+bx+c经过点A(-3,0),B(4,0) 两点,则关于x的一元二次方程a(x-1)2+c=b-bx的解是 .
(2017~2022)
(贵阳6年2考,遵义6年2考,毕节6年3考)
1.(2022·黔东南州7题4分)若二次函数y=ax2+bx+c(a≠0)的图象如图所 示,
2.(2022·毕节14题3分)在平面直角坐标系中,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ①abc>0;②2a-b=0;③9a+3b+c>0;④b2>4ac;⑤a+c
4.(2021·贵阳13题3分)二次函数y=x2的图象开口方向是 (填 “向上”或“向下”).
5.(2021·黔东南州20题3分)如图,二次函数y=ax2+bx+c(a≠0)的函数 象经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1
(贵阳6年2考,毕节6年1考)
6.(2018·毕节7题3分)将抛物线y=x2向左平移2个单位,再向下平移5个单 位,平移后所得新抛物线的表达式为 ( ) A.y=(x+2)2-5B.y=(x+2)2+5 C.y=(x-2)2-5D.y=(x-2)2+5
7.(2021·黔东南州7题4分)如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有 一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向 下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为 ( ) A.1 B.2 C.3 D.4
8.(2022·黔东南州18题3分)在平面直角坐标系中,将抛物线y=x2+2x-1 先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标 是 .
(贵阳6年4考,毕节6年2考)
9.(2021·铜仁8题4分)已知直线y=kx+2过一、二、三象限,则直线 y=kx+2与抛物线y=x2-2x+3的交点个数为( ) A.0个B.1个 C.2个D.1个或2个
10.(2021·贵阳10题3分)已知二次函数y=ax2+bx+c的图象经过(-3,0)与 (1,0)两点,关于x的方程ax2+bx+c+m=0(m>0)有两个根,其中一个根是3. 则关于x的方程ax2+bx+c+n=0(0
中考数学一轮复习课时讲解课件第14讲《二次函数的图象与性质》(含答案): 这是一份中考数学一轮复习课时讲解课件第14讲《二次函数的图象与性质》(含答案),共29页。PPT课件主要包含了-6<M<6,x-1或x4,-3≤a≤1等内容,欢迎下载使用。
中考总复习数学 第三章 第 5 讲 二次函数的图象与性质课件: 这是一份中考总复习数学 第三章 第 5 讲 二次函数的图象与性质课件,共44页。PPT课件主要包含了中考导航,中考热身,要点梳理,·1·,能力冲浪,考题透析,·2·,·3·,要点归纳,·4·等内容,欢迎下载使用。
初中数学中考复习 第14讲 二次函数的图象与性质课件PPT: 这是一份初中数学中考复习 第14讲 二次函数的图象与性质课件PPT












