2024年中考数学复习课件---第27讲　图形的对称(含折叠)、平移与旋转

这是一份2024年中考数学复习课件---第27讲　图形的对称(含折叠)、平移与旋转，共43页。PPT课件主要包含了栏目导航，轴对称图形，中心对称图形，作图步骤，轴对称，轴对称与中心对称，对称的作图步骤，图形的折叠，图形的平移，网格中图形变换作图等内容，欢迎下载使用。

1.通过具体实例理解轴对称的概念,探索它的基本性质:成轴对称的两个图形,对应点的连线被对称轴垂直平分. 2.能画出简单平面图形(点、线段、直线、三角形等)关于给定对称轴的对称图形. 3.理解轴对称图形的概念;探索等腰三角形、矩形、菱形、正多边形、圆的轴对称性质. 4.认识并欣赏自然界和现实生活中的轴对称图形.
5.了解中心对称、中心对称图形的概念,探索它们的基本性质:成中心对称的两个图形,对应点的连线经过对称中心,且被对称中心平分. 6.探索线段、平行四边形、正多边形、圆的中心对称性质. 7.认识并欣赏自然界和现实生活中的中心对称图形. 8.通过具体实例认识平移,探索它的基本性质:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等. 9.认识并欣赏平移在自然界和现实生活中的应用.
10.通过具体实例认识平面图形关于旋转中心的旋转,探索它的基本性质:一个图形和旋转得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等. 11.运用图形的轴对称、旋转、平移进行图案设计.
教材链接人教:七下P28~P33,P75~P82　八上P57~P74,P85~P93　九上P59~P77北师:七下P114~P134　八上P68~P70　八下P64~P90湘教:七下P80~P85,P112~P131　八下P51~P54
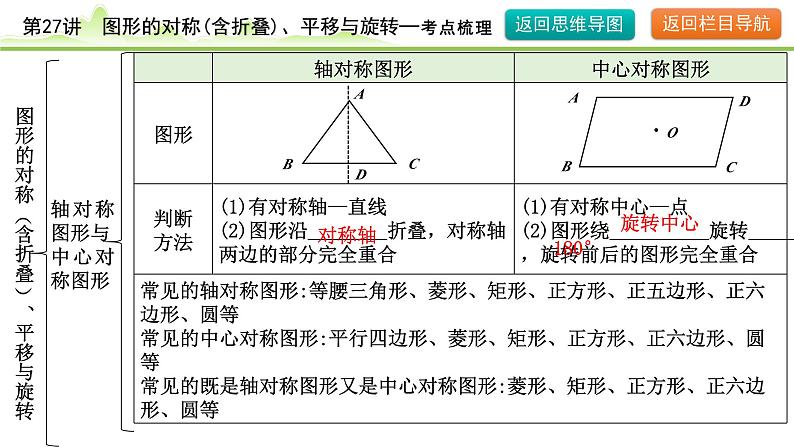
图形的对称（含折叠）、平移与旋转
轴对称图形与中心对称图形
对称的作图步骤:(1)找出原图形的关键点; (2)作出关键点关于对称轴(或对称中心)的对应点; (3)按照原图形依次连接得到的各关键点的对应点,即得到对称后 的图形
(1)位于折痕两侧的图形关于折痕成 图形(2)折叠前后的两部分图形全等,对应边、角、线段、周长、面积都分别相等(3)折叠前后对应点的连线被折痕
定义:在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这 样的图形运动叫做平移.平移不改变图形的 和
要素：平移的 和
(1)平移前后,对应线段 ,对应角相等;(2)各对应点所连接的线段 (或在同一条直线上)且相等;(3)平移前后的图形全等
(1)根据题意,确定平移的方向和平移的距离;(2)找出原图形的关键点;(3)按平移方向和平移距离平移各个关键点,得到各关键点的对应点;(4)按原图形依次连接各对应点,得到平移后的图形
定义:把一个平面图形绕着平面内某一点O转动一个角度,叫做图形 的旋转.点O叫做旋转中心,转动的角叫做旋转角.三大要素:旋 转中心,旋转方向和
(1)对应点到旋转中心的距离相等; (2)每对对应点与旋转中心所连线段的夹角都等于 ; (3)旋转前后的图形
【易错提示】图形的对称、平移、旋转,不改变图形的大小和形状, 只改变图形位置
1.找出图形的关键点;2.按要求找出各关键点经过对称、平移、旋转后的对应点;3.按原图顺次连接得到的各对应点,从而得到所求作的图形
(1)根据题意,确定旋转中心、旋转方向及旋转角; (2)找出原图形的关键点; (3)连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点; (4)按原图形依次连接各对应点,得到旋转后的图形
例1 如图,在矩形ABCD中,已知BC=2AB=8,点P是边BC上的一个动点(不与点B,C重合),连接AP,把△ABP沿着AP折叠后,点B落在点E处,连接CE,设BP=m.
(1)当m=4时,在图2中画出折叠后的图形,试判断△PCE的形状,并说明理由;
解:(1)如图1所示. △PCE是等腰直角三角形.理由: ∵m=4,BC=2AB=8,BP=m,∴AB=BP=PC=4.∵四边形ABCD是矩形,∴∠B=90°.∴∠APB=∠BAP=45°.∵△ABP沿着AP折叠,∴∠APB=∠APE=45°,PE=BP=4.∴∠BPE=∠APB+∠APE=90°,PE=PC.∴∠EPC=90°.∴△PCE是等腰直角三角形.
(2)当AE平分∠DAP时,请在备用图中作出折痕AP(尺规作图,保留作图痕迹,不写作法),并直接写出m的值.
研究折叠问题的基本思路1. 关注“全等”——明确对应线段、对应角之间的相等关系.2. 关注“折痕”——基于“垂直平分线”与“角平分线”挖掘隐含信息.3. 关注“原图形”——将所得结论与原图形的性质相结合,展开充分联想.
3.(2022·毕节大方县二模)如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF,EF.若MF=AB,则∠DAF=　　　　°. 
例2 如图1,等边三角形ABC的边长为4,D是边BC上一动点,连接AD.
(1)①如图1,将△ACD绕点A逆时针旋转得到△ABE,则旋转角度为　 　 . ②若∠BAD=45°,则∠BAE为　　　　°. ③若BD=3,则BE的长为　　　　. ④若P为边AB的中点,连接PE,则PE的最小值为　　. 
(2)如图2,若D是BC的中点,将△ABD绕点D逆时针旋转30°得到△A'B’D,A'B'与AD交于点E,求AE的长.
(3)如图3,以点C为原点建立平面直角坐标系,边CB在x轴上,将△AOB绕O点按逆时针方向旋转90°得到△A'OB',求点A'的坐标.
4.(2022·贵阳花溪区模拟)如图,Rt△ABC中,已知∠C=90°, ∠A=50°,点D在AC边上,AD=2CD,线段AD绕着点D逆时针旋转α(0°<α<180°)后,如果点A恰好落在Rt△ABC的边上,那么α的度数是(　　)A.50°或120° B.50°或60°C.80°或60° D.80°或120°
6.(2022·贵阳观山湖区一模)如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转得到正方形OA'B'C',连接BC',当点A'恰好落在直线BC'上时,线段BC'的长度是　　 　　. 
（2017~2022）
1.(2022·毕节2题3分)下列垃圾分类标识的图形中,既是中心对称图形又是轴对称图形的是(　　)
对称图形的识别(贵阳6年1考,遵义6年2考,毕节6年3考)
2.(2019·贵阳5题3分)如图,在3×3的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是(　 　)
3.(2022·六盘水8题3分)如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到(　　)
A.三角形　 B.梯形 C.正方形　 D.五边形
与折叠有关的计算(贵阳6年2考,遵义6年3考,毕节6年2考)
7.(2020·黔西南州16题3分)如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上点G处,并使折痕经过点A,已知BC=2,则线段EG的长度为　　　　. 
8.(2018·遵义18题4分)如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B,D重合),折痕为EF,若DG=2,BG=6,则BE的长为　　　　. 
9.(2020·铜仁17题4分)如图,在矩形ABCD中,AD=4,将∠A向内翻折,点A落在BC上,记为A1,折痕为DE.若将∠B沿EA1向内翻折,点B恰好落在DE上,记为B1,则AB=　　　　.
10.(2022·黔东南州20题3分)如图,折叠边长为4 cm的正方形纸片ABCD,折痕是DM,点C落在点E处,分别延长ME,DE交AB于点F,G,若M是BC边的中点,则FG=　　　　cm. 
利用对称求最值(毕节6年1考)
11.(2021·毕节18题5分)如图,在菱形ABCD中,BC=2,∠C=120°,Q为AB的中点,P为对角线BD上的任意一点,则AP+PQ的最小值为　　　　. 
13.(2017·毕节14题3分)如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是(　　)A.△AEE'是等腰直角三角形 B.AF垂直平分EE'C.△E'EC∽△AFD D.△AE'F是等腰三角形
与旋转有关的计算(毕节6年1考)
15.(2017·黔南州18题4分)如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB,CA1相交于点D,则线段BD的长为　　　　.