2023-2024学年广东省深圳市福田中学高三（下）开学数学试卷（含解析）

这是一份2023-2024学年广东省深圳市福田中学高三（下）开学数学试卷（含解析），共16页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.已知集合A={x∈Z|x2+2x−3⩽0}，B={x|x⩾−1}，则集合A∩B的元素个数为( )
A. 1B. 2C. 3D. 4
2.已知复数z满足(1−i)⋅z=3+i.其中i为虚数单位，则|z−|=( )
A. 3B. 3C. 5D. 5
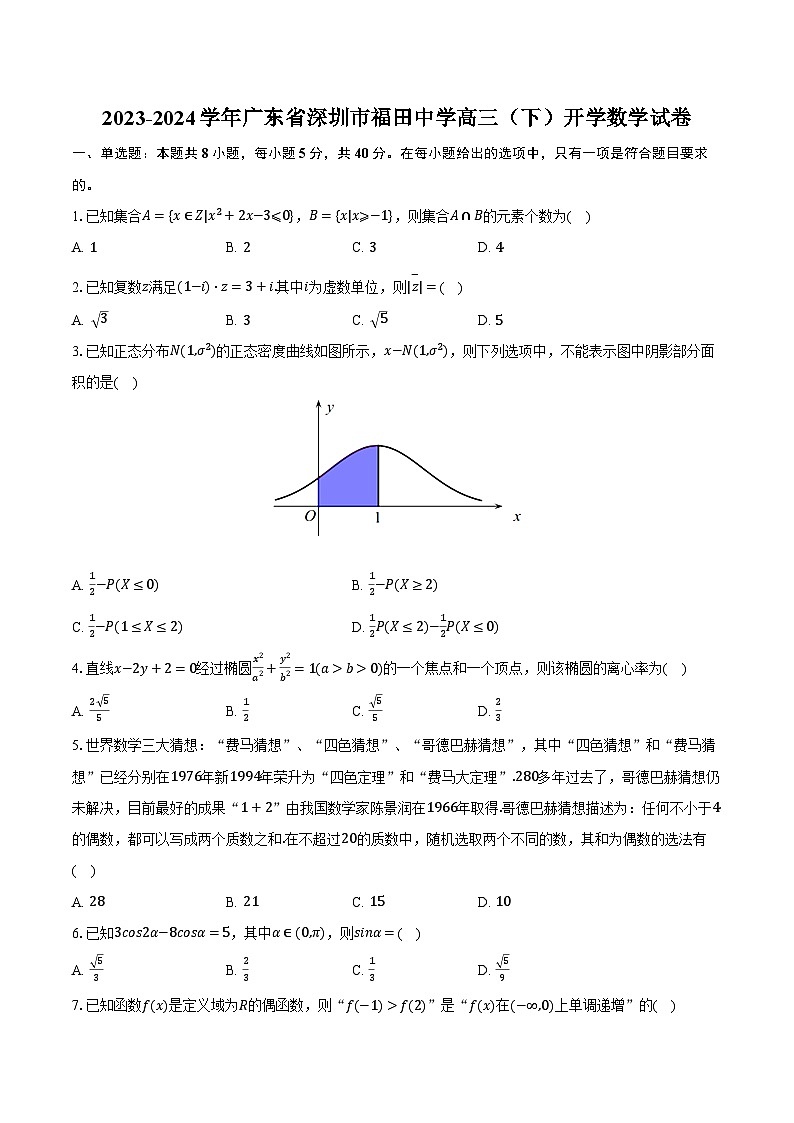
3.已知正态分布N(1,σ2)的正态密度曲线如图所示，x−N(1,σ2)，则下列选项中，不能表示图中阴影部分面积的是( )
A. 12−P(X≤0)B. 12−P(X≥2)
C. 12−P(1≤X≤2)D. 12P(X≤2)−12P(X≤0)
4.直线x−2y+2=0经过椭圆x2a2+y2b2=1(a>b>0)的一个焦点和一个顶点，则该椭圆的离心率为( )
A. 2 55B. 12C. 55D. 23
5.世界数学三大猜想：“费马猜想”、“四色猜想”、“哥德巴赫猜想”，其中“四色猜想”和“费马猜想”已经分别在1976年新1994年荣升为“四色定理”和“费马大定理”.280多年过去了，哥德巴赫猜想仍未解决，目前最好的成果“1+2”由我国数学家陈景润在1966年取得.哥德巴赫猜想描述为：任何不小于4的偶数，都可以写成两个质数之和.在不超过20的质数中，随机选取两个不同的数，其和为偶数的选法有( )
A. 28B. 21C. 15D. 10
6.已知3cs2α−8csα=5，其中α∈(0,π)，则sinα=( )
A. 53B. 23C. 13D. 59
7.已知函数f(x)是定义域为R的偶函数，则“f(−1)>f(2)”是“f(x)在(−∞,0)上单调递增”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
8.设a≠0，若x=a为函数f(x)=a(x−a)2(x−b)的极大值点，则( )
A. abC. aba2
二、多选题：本题共3小题，共15分。在每小题给出的选项中，有多项符合题目要求。
9.有一组样本数据x1，x2，…，xn，由这组数据得到新样本数据y1，y2，…，yn，其中yi=xi+c(i=1,2,…,n)，c为非零常数，则( )
A. 两组样本数据的样本平均数相同B. 两组样本数据的样本中位数相同
C. 两组样本数据的样本标准差相同D. 两组样数据的样本极差相同
10.设数列{an}的前n项和为Sn，且满足a1=1,an+1=2an,n为奇数1an,n为偶数，则下列说法中正确的有( )
A. a6=2B. 数列{an}为递增数列
C. a2022=12D. S20=22.5
11.已知O为坐标原点，椭圆C：x216+y29=1的左、右焦点分别为F1、F2，椭圆的上顶点和右顶点分别为A、B，点P、Q都在C上，且PO=OQ，则下列说法正确的是( )
A. △PQF2周长的最小值为14B. 四边形PF1QF2可能是矩形
C. 直线PB，QB的斜率之积为定值−916D. △PQF2的面积最大值为3 7
三、填空题：本题共4小题，每小题5分，共20分。
12.在(2x+a)(x+2x)6的展开式中，x2的系数为−120，则该二项展开式中的常数项为______．
13.已知向量OA=(3,2)，OB=(2,1)，O点为坐标原点，在x轴上找一个点M，使得AM⋅BM取最小值，则M点的坐标是______．
14.已知函数f(x)=2sinωx(ω>0)在区间[−3π4,π4]上单调递增，且直线y=−2与函数f(x)的图象在[−2π,0]上有且仅有一个交点，则实数ω的取值范围是______．
15.已知三棱锥P−ABC的四个顶点都在球O的球面上，PB=PC，∠PAB=90°，△ABC是边长为2 3的等边三角形，△PBC的面积为5 3，则球O的体积为______．
四、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题10分)
在△ABC中，角A，B，C所对的边分别为a，b，c.已知a= 6，b=2c，csA=−14．
(1)求c的值；
(2)求sin B的值；
(3)求sin(2A−B)的值．
17.(本小题12分)
设等差数列{an}前n项和Sn，a1=1，满足2Sn+1=n(an+5)+2，n∈N⋅．
(1)求数列{an}的通项公式；
(2)记bn=n+1SnSn+2，设数列{bn}的前n项和为Tn，求证Tn<516．
18.(本小题12分)
如图，已知四棱锥P−ABCD，BC/​/AD，平面PAD⊥平面PBA，且DP=DB，AB=BP=PA=AD=2BC．
(1)证明：AD⊥平面PBA；
(2)求直线AB与平面CDP所成角的正弦值．
19.(本小题12分)
在一次活动课上，老师准备了4个大小完全相同的红包，其中只有一个红包里面有100元，其余三个里面都是白纸．老师邀请甲上台随机抽取一个红包，但不打开红包，然后老师从剩下的三个红包中拿走一个装有白纸的红包，甲此时可以选择将自己选中的红包与剩下的两个红包中的一个进行置换．
(1)若以获得有100元的红包概率的大小作为评判的依据，甲是否需要选择置换？请说明理由．
(2)以(1)中的结果作为置换的依据，记X表示甲获得的金额，求X的分布列与期望．
20.(本小题12分)
在平面直角坐标系xOy中，椭圆C：x2a2+y2b2=1(a>b>0)的左，右顶点分别为A、B，点F是椭圆的右焦点，AF=3FB，AF⋅FB=3.⋅
(1)求椭圆C的方程；
(2)经过椭圆右焦点F且斜率不为零的动直线l与椭圆交于M、N两点，试问x轴上是否存在异于点F的定点T，使|MF|⋅|NT|=|NF|⋅|MT|恒成立？若存在，求出T点坐标，若不存在，说明理由．
21.(本小题12分)
已知函数f(x)=ex+sinx−csx，f′(x)为f(x)的导数．
(1)证明：当x>0时，f′(x)≥2；
(2)设g(x)=f(x)−2x−1，证明：g(x)有且仅有2个零点．
答案和解析
1.【答案】C
【解析】解：∵A={x∈Z|x2+2x−3⩽0}={x∈Z|−3⩽x⩽1}={−3,−2,−1,0,1}，又B={x|x⩾−1}，
∴A∩B={−1,0,1}，即集合A∩B的元素个数为3．
故选：C．
结合一元二次不等式求集合A，再利用集合的交集运算，即可求解．
本题主要考查交集及其运算，属于基础题．
2.【答案】C
【解析】解：由题意，z=3+i1−i=(3+i)(1+i)(1−i)(1+i)=1+2i，
则z−=1−2i，|z−|= 1+4= 5．
故选：C．
化简复数z，进而可得z的共轭复数的模长．
本题考查复数的模长，属于基础题．
3.【答案】C
【解析】解：因为该正态分布曲线关于直线x=1对称，所以阴影部分面积为P(0≤X≤1)=12[1−2P(X≤0)]=12−P(X≤0)或
12[1−2P(X≥2)]=12−P(X≥2)或12[P(X≤2)−P(X≤0)]=12P(X≤2)−12P(X≤0)，所以ABC能表示阴影部分面积；
C不能表示阴影部分面积．
故选：C．
根据该正态分布曲线关于直线x=1对称可解决此题．
本题考查正态分布曲线应用，考查数学运算能力，属于基础题．
4.【答案】A
【解析】【分析】
本题考查了椭圆的基本性质，只需根据已知条件求出a，b，c即可，属于基础题型．
直线x−2y+2=0与坐标轴的交点为(−2,0)，(0,1)，依题意得c=2,b=1⇒a= 5⇒e=2 55．
【解答】
直线x−2y+2=0与坐标轴的交点为(−2,0)，(0,1)，
直线x−2y+2=0经过椭圆x2a2+y2b2=1(a>b>0)的一个焦点和一个顶点；
故c=2,b=1⇒a= 5⇒e=2 55．
故选：A．
5.【答案】B
【解析】【分析】
本题考查排列组合问题，属基础题．
求出不超过20的质数，再利用组合列式求解作答．
【解答】
解：依题意，不超过20的质数有：2，3，5，7，11，13，17，19，
从中随机选取两个不同的数，其和为偶数，
即是从3，5，7，11，13，17，19中任取两个，
所以不同选法种数是C72=21．
故选：B．
6.【答案】A
【解析】【分析】
本题主要考查了二倍角公式及同角三角函数关系，属于基础题．
由已知结合二倍角公式先求出csα，然后结合同角平方关系求解．
【解答】
解：因为3cs2α−8csα=6cs2α−3−8csα=5，
所以csα=−23或csα=2(舍)，
因为α∈(0,π)，所以sinα= 1−cs2α= 53．
故选：A．
7.【答案】B
【解析】解：由题意，函数f(x)的定义域为R的偶函数，当“f(−1)>f(2)”时，
根据偶函数，f(−1)>f(2)=f(−2)，但是，“f(x)在(−∞,0)不一定单调递增”；
当“f(x)在(−∞,0)上单调递增”时，有f(−1)>f(−2)=f(2)，
故“f(−1)>f(2)”是“f(x)在(−∞,0)上单调递增”的必要不充分条件．
故选：B．
直接利用函数的单调性和函数的值的关系，利用充分条件和必要条件的应用求出结果．
本题考查充分必要条件，考查函数的单调性，属于基础题．
8.【答案】D
【解析】【分析】
本题考查利用导数研究函数的极值、极值点，考查一元二次不等式的解法，考查分类讨论思想，属于较难题．
根据a≠0，且x=a为函数fx=ax−a2x−b的极大值点，利用导数来判断a，b该满足的条件，为此需要判断函数在x=a左右的单调性，本题需要分a=b，a>0并且a0，并且a>b，a<0，并且ab共5种情况讨论，由此可以推出：a>0并且ab，然后可判断选项的正确性．
【解答】
解：因为a≠0，
(Ⅰ)所以当a=b时，函数fx=ax−a3在−∞,+∞单调，无极值，不合条件；
(Ⅱ)当a≠b时，因为f′x=3ax−ax−a+2b3，
所以，①若a>0并且a由f′x>0，得：xa+2b3，
由f′x<0，得：a所以这时fx在−∞,a上单调递增，在a,a+2b3上单调递减，x=a是函数fx的极大值点，符合条件；
②若a>0，并且a>b时，a>a+2b3，
由f′x>0，得：xa，
由f′x<0，得：a+2b3所以这时fx在a+2b3,a上单调递减，在a,+∞上单调递增，x=a是函数fx的极小值点，不符合条件；
③若a<0，并且a由f′x>0，得：a由f′x<0，得：xa+2b3，
这时fx在−∞,a上单调递减，在a,a+2b3上单调递增，x=a是函数fx的极小值点，不符合条件；
④若a<0，并且a>b时，a>a+2b3，
由f′x>0，得：a+2b3由f′x<0，得：xa，
所以这时fx在a+2b3,a上单调递增，在a,+∞上单调递减，x=a是函数fx的极大值点，符合条件；
因此，若x=a为函数fx=ax−a2x−b的极大值点，则a，b必须满足条件：
a>0并且ab．
由此可见，A，B均错误；
又总有ab−a2=ab−a>0成立，所以C错误，D正确．
故选D．
9.【答案】CD
【解析】解：对于A，E(y)=E(x+c)=E(x)+c，
∴两组样本数据的样本平均数不相同，故A错误；
对于B，若样本数据x1，x2，…，xn的中位数为xn，
则新样本数据y1，y2，…，yn，其中yi=xi+c(i=1,2,…,n)，
c为非零常数的中位数为xn+c，故B错误；
对于C，D(y)=D(x+c)=D(x)，∴两组样本数据的样本标准差相同，故C正确；
对于D，若样本数据x1，x2，…，xn的极差数为xa−xb，
则新样本数据y1，y2，…，yn，其中yi=xi+c(i=1,2,…,n)，
c为非零常数的中位数为(xa+c)−(xb+c)=xa−xb，故D正确．
故选：CD．
由yi=xi+c(i=1,2,…,n)，c为非零常数，利用样本平均数、中位数、标准差、极差的定义直接求解．
本题考查样本平均数、中位数、标准差、极差的定义等基础知识，考查运算求解能力，是基础题．
10.【答案】AD
【解析】解：由题意，数列{an}满足a1=1,an+1=2an,n为奇数1an,n为偶数，
当n=1时，a2=2a1=2；当n=2时，a3=1a2=12；当n=3时，a4=2a3=1；
当n=4时，a5=1a4=1；当n=5时，a6=2a5=2；当n=6时，a7=1a6=12；⋯⋯，
归纳可得数列{an}构成以1,2,12,1为周期的周期数列，所以a6=a2=2，A正确，B不正确；
又由a2022=a505×4+2=a2=2，所以C不正确；
因为a1+a2+a3+a4=2+12+1+1=92，所以S20=5×92=22.5，所以D正确．
故选：AD．
根据题意，分别求得a1，a2，a3，a4，a5，⋯，得到数列{an}构成以1,2,12,1为周期的周期数列，逐项判定，即可求解．
本题主要考查数列递推关系式的应用，考查计算能力，属于中档题．
11.【答案】ACD
【解析】解：由PO=OQ，可知P，Q关于原点对称，
对于A，根据椭圆的对称性，|PQ|+|PF2|+|QF2|=|PQ|+|PF2|+|PF1|=|PQ|+8，
当PQ为椭圆的短轴时，|PQ|有最小值6，所以△PQF2周长的最小值为14，故A正确；
对于B，因为tan∠F1AO=cb= 73，所以∠F1AO<π4，
则∠F1AF2<π2，故椭圆上不存在点P，使得∠F1PF2=π2，
又四边形PF1QF2是平行四边形，所以四边形PF1QF2不可能是矩形，故B不正确；
对于C，由题意得B(4,0)，设P(x,y)，则Q(−x,−y)，
所以kPB⋅kQB=yx−4⋅−y(−x)−4=y2x2−16=9(1−x216)x2−16=−916，故C正确；
对于D，设△PF2Q的面积为S=12|OF||yP−yQ|，所以当PQ为椭圆的短轴时，|yP−yQ|=6最大，
所以S=12|OF||yP−yQ|≤12× 7×6=3 7，故D正确．
故选：ACD．
对四个选项一一判断：对于A：利用椭圆的对称性，判断出PQ为椭圆的短轴时，△PQF2周长最小即可判断；对于B：判断出∠F1AF2<π2，从而四边形PF1QF2不可能是矩形即可判断；对于C：设P(x,y)，直接计算出kPB⋅kQB=−916，即可判断；对于D：由△PF2Q的面积为S=12|OF||yP−yQ|，即可判断．
本题考查了椭圆的性质，属于中档题．
12.【答案】−320
【解析】解：根据(x+2x)6的展开式Tr+1=C6r⋅2r⋅x6−2r，(r=0,1,2,3,4,5,6)，
当与2x配对时，不存在x2项，
当与a配对时，令r=2时，故系数为C62⋅22⋅a=−120，解得a=−2；
故关系式为(2x−2)(x+2x)6，
当与−2配对时，则r=3，常数项为(−2)C63⋅23=−320．
故答案为：−320．
直接利用二项式的展开式求出结果．
本题考查的知识要点：二项式的展开式，组合数，主要考查学生的运算能力，属于基础题．
13.【答案】(52,0)
【解析】解：设点M(m,0)，AM=(m−3,−2)，BM=(m−2,−1)，
则AM⋅BM=(m−3,−2)⋅(m−2,−1)=m2−5m+8=(m−52)2+74，
故m=52时，AM⋅BM取最小值，
此时，点M的坐标为(52,0)，
故答案为：(52,0)．
设点M的坐标，计算AM⋅BM 的结果，再利用二次函数求最值即可．
本题考查向量的数量积公式的应用，二次函数求最值，属于中档题．
14.【答案】[14,23]
【解析】解：∵函数f(x)=2sinωx(ω>0)在区间[−3π4,π4]上单调递增，
∴ω×(−3π4)≥−π2，且ω×π4≤π2，求得0<ω≤23．
且直线y=−2与函数f(x)的图象在[−2π,0]上有且仅有一个交点，
ωx∈[−2ωπ,0]，
∴−5π2<−2ωπ≤−π2，求得14≤ω<54．
综上可得，实数ω的取值范围为[14,23]，
故答案为：[14,23].
由题意利用正弦函数的图象和性质，求得实数ω的取值范围．
本题主要考查正弦函数的图象和性质，属于中档题．
15.【答案】64 2π3
【解析】解：已知三棱锥P−ABC的四个顶点都在球O的球面上，PB=PC，∠PAB=90°，△ABC是边长为2 3的等边三角形，
如图所示：
设底面等边ΔABC的中心为H，过点H作平面ABC的垂线和PA的中垂线交于点O，即三棱锥P−ABC的外接球的球心；
由于AB=AC，AP=AP，PB=PC，所以△PAB≌△PAC，
由于△ABC是边长为2 3的等边三角形，
故12×2 3×PD=5 3，解得PD=5；
故PB= 52+( 3)2= 28，
所以PA= ( 28)2−(2 3)2=4，
故AO= 22+22=2 2，
故V球=43⋅π⋅(2 2)3=64 2π3．
故答案为：64 2π3．
首先利用三角形的全等的判定得到△PAB≌△PAC，进一步利用三角形的面积公式求出PD的值，进一步求出三棱锥的外接球的半径，最后求出球的体积．
本题考查的知识要点：三角形的全等的判定，三角形的面积公式，三棱锥和球的关系，球的体积公式，主要考查学生的理解能力和计算能力，属于中档题．
16.【答案】解(1)因为a= 6，b=2c，csA=−14，
由余弦定理可得csA=b2+c2−a22bc=4c2+c2−64c2=−14，
解得：c=1；
(2)csA=−14，A∈(0,π)，所以sinA= 1−cs2A= 154，
由b=2c，可得sinB=2sinC，
由正弦定理可得asinA=csinC，即 6 154=1sinC，
可得sinC= 108，
所以sinB=2sinC=2× 108= 104；
(3)因为csA=−14，sinA= 154，
所以sin2A=2sinAcsA=2×(−14)× 154=− 158，cs2A=2cs2A−1=2×116−1=−78，
sinB= 104，可得csB= 64，
所以sin(2A−B)=sin2AcsB−cs2AsinB=− 158× 64−(−78)× 104= 108，
所以sin(2A−B)的值为 108．
【解析】本题考查利用余弦定理和正弦定理解三角形，三角恒等变换的综合应用，以及由一个三角函数值求其他三角函数值，属于中档题．
(1)由余弦定理及题中条件可得c边的值；
(2)由正弦定理可得sinC的值，再由b=2c及正弦定理可得sinB的值；
(3)求出2A及B的正余弦值，由两角差的正弦公式可得2A−B的正弦值．
17.【答案】解：(1)依题意有2(a1+a2)=a1+5+2，
∵a1=1，∴a2=3，
又{an}为等差数列，设公差为d，
∴d=a2−a1=2，∴an=1+2(n−1)=2n−1．
(2)证明：由(1)可得Sn=(1+2n−1)n2=n2，
∴bn=n+1n2(n+2)2=14(1n2−1(n+2)2)，
b1=14(11−132)，b2=14(122−142)，b3=14(132−152)，⋯，bn−1=14(1(n−1)2−1(n+1)2)，
bn=14(1n2−1(n+2)2)，
∴Tn=14(1+14−1(n+1)2−1(n+2)2)<14×54=516．
【解析】(1)根据等差数列的通项公式进行求解即可；
(2)利用等差数列的前n项和公式，结合裂项相消法进行求解即可得证．
本题考查等差数列的通项公式和求和公式，以及数列的裂项相消求和，考查转化思想和运算能力、推理能力，属于中档题．
18.【答案】(1)证明：分别取PA，PB的中点M，N，连接AN，DN，BM，
因DP=DB，N为PB的中点，所以PB⊥DN．
同理，PB⊥AN，BM⊥PA，所以PB⊥平面DNA，所以PB⊥AD，
因为平面PAD⊥平面PBA，
平面PAD∩平面PBA=PA，BM⊆平面PBA，BM⊥PA，
故BM⊥平面PAD，则BM⊥AD，又因为PB，BM是平面PBA中的相交直线，
所以AD⊥平面PBA．
(2)解：设直线AB和DC交于点Q，
连结PQ，则PQ⊥PA，
因平面ADP⊥平面ABP，故PQ⊥平面PAD，
则平面PQD⊥平面PAD，
取PD的中点G，连结AG，QG，则AG⊥平面PQD，
所以∠AQG就是直线AB与平面PCD所成角．
不妨设AB=2，则在Rt△AGQ中，AG= 2，AQ=4，
故sin∠AQG=AGAQ= 24，
所以直线AB与平面PCD所成角的正弦值为 24．
【解析】(1)要据面面垂直所需的线面垂直，逐一找出符合条件的线线垂直，即可证明；
(2)根据线面角的定义，找出线段AB的射影，构成所求线面角，利用锐角三角函数求解．
(1)本题考查线面垂直的判定，面面垂直的判定和性质定理，属于中档题；
(2)本题考查线面角的求解，考查线面角的定义，属于基础题．
19.【答案】解：(1)甲需要选择置换；
理由如下：若甲同学不选择置换，则获得有100元的红包的概率为14，
若甲同学选择置换，则获得有100元的红包的概率为34×12=38，
因为38>14，所以甲需要选择置换．
(2)X的可能取值为0，100，
P(X=100)=38，P(X=0)=1−38=58，
X的分布列如下：
EX=0×58+100×38=37.5．
【解析】本题考查了古典概型和离散型随机变量的分布列和数学期望，属于中档题．
(1)根据古典概型即可得到答案．
(2)由题可得X的可能取值为0，100，分别求概率，即可得分布列，计算可得期望．
20.【答案】解：(1)由题意知，A(−a,0)，B(a,0)，F(c,0)，
因为AF=3FB，AF⋅FB=3，
所以a+c=3(a−c)(a+c)(a−c)=3，解得a=2c=1，从而b2=a2−c2=3，
所以椭圆C的方程为：x24+y23=1；
(2)如图，

由椭圆右焦点F(1,0)，故可设直线l的方程为x=my+1，设M(x1,y1)，N(x2,y2)，
联立方程组x=my+1x24+y23=1，整理得(3m2+4)y2+6my−9=0，
则Δ=36m2−4×(−9)(3m2+4)=144(m2+1)>0，
且y1+y2=−6m3m2+4，y1y2=−93m2+4，
设存在点T，设T点坐标为(t,0)，
由|MF||NT|=|NF||MT|，可得|MF||NF|=|MT||NT|，
又因为|MF||NF|=S△TFMS△TFN=12|FT||MT|sin∠MTF12|FT||NT|sin∠NTF=|MT|sin∠MTF|NT|sin∠NTF，
所以sin∠MTF=sin∠NTF，所以∠MTF=∠NTF，
所以直线TM和TN关于x轴对称，其倾斜角互补，即有kMT+kNT=0，
则kMT+kNT=y1x1−t+y2x2−t=0，
所以y1(x2−t)+y2(x1−t)=0，
所以y1(my2+1−t)+y2(my1+1−t)=0，
整理得2my1y2+(1−t)(y1+y2)=0，
即2m×−93m2+4+(1−t)×−6m3m2+4=0，
即3m3m2+4+(1−t)×m3m2+4=0，
解得t=4，符合题意，
即存在点T(4,0)满足题意．
【解析】(1)根据椭圆的顶点及焦点坐标，利用向量关系建立方程求出a，c得解；
(2)根据条件可转化为kMT+kNT=0，再由根与系数的关系代入化简即可得解．
本题考查椭圆方程的求法及直线与椭圆的综合应用，属于中档题．
21.【答案】证明：(1)∵f(x)=ex+sinx−csx，
∴f′(x)=ex+csx+sinx，
令h(x)=ex+csx+sinx，则h′(x)=ex−sinx+csx，
当x>0时，设p(x)=ex−x−1，q(x)=x−sinx，
∵p′(x)=ex−1>0，q′(x)=1−csx>0，
∴p(x)和q(x)在[0,+∞)上单调递增，
即p(x)≥p(0)=0，q(x)≥q(0)=0，
∴当x>0时，ex>x+1，x>sinx，
则h′(x)=ex−sinx+csx>x+1−sinx+csx=(x−sinx)+(1+csx)>0，
所以h(x)=ex+csx+sinx在[0,+∞)上单调递增，
所以h(x)≥h(0)=2，即当x≥0时，f′(x)≥2．
(2)由已知得g(x)=ex+sinx−csx−2x−1，
①当x≥0时，因为g′(x)=ex+csx+sinx−2=f′(x)−2≥0，
所以g(x)在[0,+∞)上单调递增，
又因为g(0)=−1<0，g(π)=eπ−2π>0，
所以由零点存在性定理可知g(x)在[0,+∞)上仅有一个零点，
②当x<0时，设m(x)=2−sinx−csxex(x<0)，则m′(x)=2(sinx−1)ex≤0，
所以m(x)在(−∞,0)上单调递减，
所以m(x)>m(0)=1，所以ex+csx+sinx−2<0，
所以g′(x)=ex+csx+sinx−2<0，
所以g(x)在(−∞,0)上单调递减，
又因为g(0)=−1<0，g(−π)=e−π+2π>0，
所以由零点存在性定理可知g(x)在(−∞,0)上仅有一个零点，
综上所述，g(x)有且仅有2个零点．
【解析】(1)令h(x)=ex+csx+sinx，利用导数判断h( x)的单调性，并求出其最小值即可证明；
(2)由(1)可知，g(x)在[0,+∞)上单调递增，利用零点存在性定理可证明在这个区间上有一个零点，通过构造函数，即可证明g(x)在(−∞,0)上单调递减，同理利用零点存在性定理可证明在这个区间上有一个零点．
本题主要考查利用导数研究函数的单调性与最值，考查不等式的证明以及函数零点存在性定理的应用，考查分类讨论思想与逻辑推理能力，属于难题．X
0
100
P
58
38