北师大版八年级下册1 等腰三角形备课ppt课件

这是一份北师大版八年级下册1 等腰三角形备课ppt课件，共26页。PPT课件主要包含了复习回顾，激趣导入，你能证明你的结论吗，预习示疑，学习目标，合作探究，你能证明这些定理吗，测试评价，∵DEBC，∵ADAE等内容，欢迎下载使用。

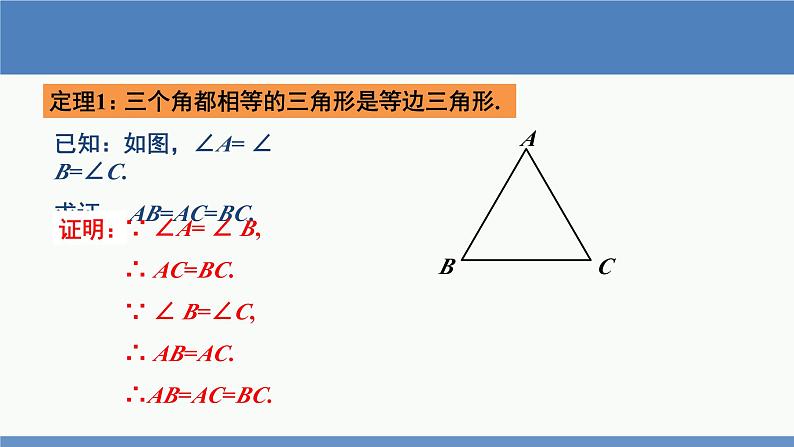
等腰三角形的判定定理：
有两个角相等的三角形是等腰三角形.(简称“等角对等边”).
用反证法证题的一般步骤:1. 假设: 先假设命题的结论不成立;2. 归谬: 从这个假设出发,应用正确的推论方法,得出与定义，公理、已证定理或已知条件相矛盾的结果;3. 结论: 由矛盾的结果判定假设不正确,从而肯定命题的结论正确.
1.能用所学的知识证明等边三角形的判定定理.(重点)2.掌握含30°角的直角三角形的性质并解决有关问题.(难点)
探究一：等边三角形的判定
由等腰三角形的判定定理，可得等边三角形的两个判定定理：
1.三个角都相等的三角形是等边三角形；2.有一个角等于60°的等腰三角形是等边三角形.
∵ ∠A= ∠ B,∴ AC=BC.∵ ∠ B=∠C,∴ AB=AC.∴AB=AC=BC.
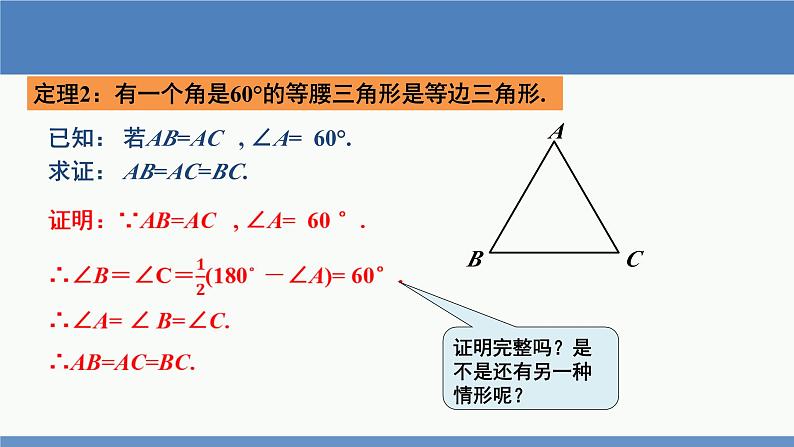
定理2：有一个角是60°的等腰三角形是等边三角形.
已知： 若AB=AC , ∠A= 60°.求证： AB=AC=BC.
证明完整吗？是不是还有另一种情形呢？
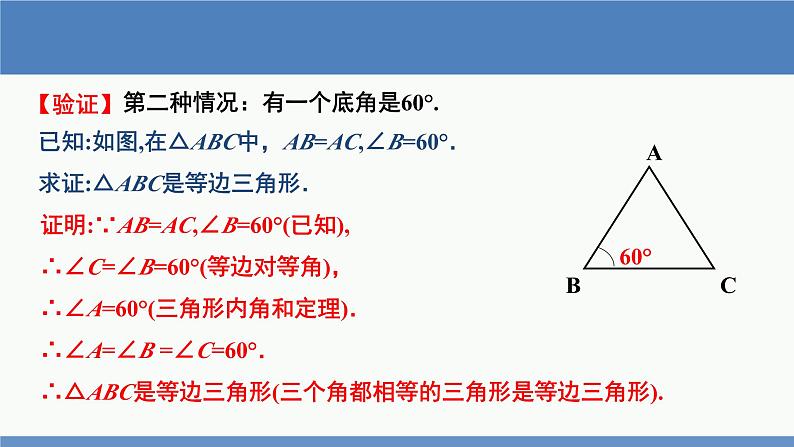
证明:∵AB=AC,∠B=60°(已知),∴∠C=∠B=60°(等边对等角)，∴∠A=60°(三角形内角和定理)．∴∠A=∠B =∠C=60°． ∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
∴ ∠A= ∠B= ∠C.
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
变式：上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
如图,在等边三角形ABC中，AD=AE, 求证：△ADE是等边三角形.
∴ ∠A= ∠B= ∠C=60°.
∴ △ADE是等腰三角形
∴ △ADE是等边三角形.
又∵ ∠A=60°.
“三线合一”,即等腰三角形顶角平分线，底边上的中线、高线互相重合
有一角是60°的等腰三角形是等边三角形
等边三角形三个内角都相等，且每个角都是60°
三个角都相等的三角形是等边三角形
探究二：含30°角的直角三角形的性质
你能说出所拼成的三角形的形状吗？
结论:在直角三角形中, 30°角所对的直角边等于斜边的一半.
分析：突破如何证明“线段的倍、分”问题
∵ ∠ACB=90°, ∠BAC=30°，∴∠ACD=90°，∠B=60°，∵AC=AC， ∴△ABC≌△ADC（SAS） ， ∴ AB=AD（全等三角形的对应边相等）. ∴△ABD是等边三角形(有一个角是60°的等腰三角形是等边三角形)，
证明: 延长BC至D,使CD=BC,连接AD.
定理:在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半．
证明:在直角三角形中, 如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°．
1.下列说法不正确的是(　　)A.三边相等的三角形是等边三角形B.三个角相等的三角形是等边三角形C.有一个角为60°的三角形是等边三角形D.顶角为60°的等腰三角形是等边三角形
∴△ABC是等边三角形.
又∵∠CDE=120°，DF平分∠CDE.
∴ ∠FDC=∠ABC=60°，
∴ △ABC是等腰三角形，
∴ ∠EDF=∠FDC=60°，
解：在Rt△ABC中，∵CD是斜边AB上的高，∴∠ADC＝90°，∴∠ACD＝∠B＝30°，∴在Rt△ACD中，AC＝2AD＝6 cm，在Rt△ABC中，AB＝2AC＝12 cm，即AB的长度是12 cm.
1.等边三角形的判定:有一个角是60°的等腰三角形是等边三角形．三个角都相等的三角形是等边三角形．
2.特殊的直角三角形的性质:在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半．
3.数学方法：分类的思想．
3.在等边三角形中，两条中线所夹的钝角的度数为 .
6.已知a，b，c是△ABC的三边，且满足关系式a2＋c2＝2ab＋2bc－2b2，试说明△ABC是等边三角形．
证明：由a2+c2=2ab+2bc-2b2，得a2＋c2－2ab－2bc＋2b2＝0，∴ a2＋b2－2ab＋c2－2bc＋b2＝0， ∴ (a－b)2＋(b－c)2＝0，∴ a－b＝0且b－c＝0，即a＝b且b＝c，∴ a＝b＝c，∴ △ABC是等边三角形．