数学八年级下册2 直角三角形教学演示课件ppt

这是一份数学八年级下册2 直角三角形教学演示课件ppt，共21页。PPT课件主要包含了复习回顾，互逆命题，互逆定理，逆定理，激趣导入，ASA，SAS，预习示疑，学习目标，合作探究等内容，欢迎下载使用。

1.勾股定理：直角三角形两条直角边的平方和等于斜边的平方；逆定理：如果 ，那么这个三角形是直角三角形.
2.在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题称为 .
3.如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为 ,其中一个定理称另一个定理的 .
三角形两边的平方和等于第三边的平方
1.判定一般三角形全等的条件有哪几种？
SSS、SAS、ASA 、 AAS.
1．探索并理解直角三角形全等的判定方法“HL”．（难点）2．会用直角三角形全等的判定方法“HL”判定两个直角三角形全等．（重点）
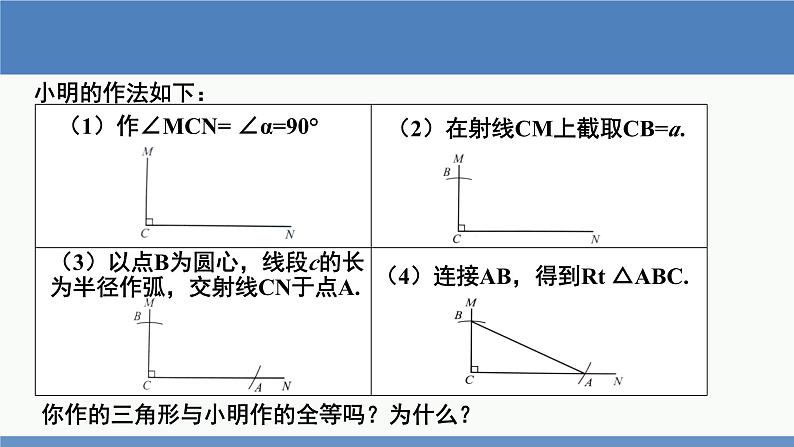
做一做：已知一条直角边和斜边，求作一个直角三角形.
探究：直角三角形全等的判定
（1）作∠MCN= ∠α=90°
（2）在射线CM上截取CB=a.
（3）以点B为圆心，线段c的长为半径作弧，交射线CN于点A.
（4）连接AB，得到Rt △ABC.
你作的三角形与小明作的全等吗？为什么？
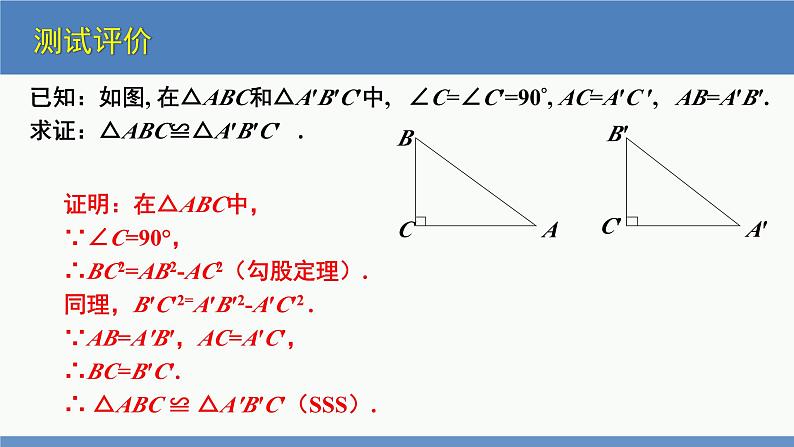
证明：在△ABC中，∵∠C=90°，∴BC2=AB2-AC2（勾股定理）.同理，B′C′2=A′B′2-A′C′2 .∵AB=A′B′，AC=A′C′，∴BC=B′C′.∴ △ABC ≌ △A′B′C′（SSS）.
“斜边、直角边”判定方法
文字语言： 斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL”）.
在Rt△ABC和Rt△ A′B′C′ 中，
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
判断下列命题的真假，并说明理由：（1）两个锐角对应相等的两个直角三角形全等（ ）（2）斜边及一锐角对应相等的两个直角三角形全等；（ ）（3）两条直角边对应相等的两个直角三角形全等；（ ）（4）两边对应相等的两个直角三角形全等； （ ）（5）一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等． （ ）
解：根据题意，可知∠BAC= ∠EDF=90°， ∴Rt △BAC≌Rt △EDF（HL） ∴ ∠B= ∠DEF（全等三角形的对应角相等） ∵ ∠DEF+ ∠F=90°（直角三角形的两锐角互余） ∴ ∠B+ ∠F=90°.
解：相等.根据题意可知，∠AOC=∠AOB=90°，AB=AC,AO=AO∴Rt△AOB≌Rt△AOC (HL)∴ OB=OC (全等三角形对应边相等)
2.下列条件中,不能判定两个直角三角形全等的是(　　)A.一个锐角和斜边分别相等B.两条直角边分别相等C.两个锐角分别相等D.斜边和一条直角边分别相等
证明: 如图,连接OP.∵PC⊥OA,PD⊥OB,∴∠PCO=∠PDO=90°.