初中数学北师大版八年级下册3 线段的垂直平分线备课课件ppt

这是一份初中数学北师大版八年级下册3 线段的垂直平分线备课课件ppt，共21页。PPT课件主要包含了激趣导入，应建在C处，你能说说你的理由吗，预习示疑，学习目标，合作探究，知识要点，文字语言，符号语言，测试评价等内容，欢迎下载使用。

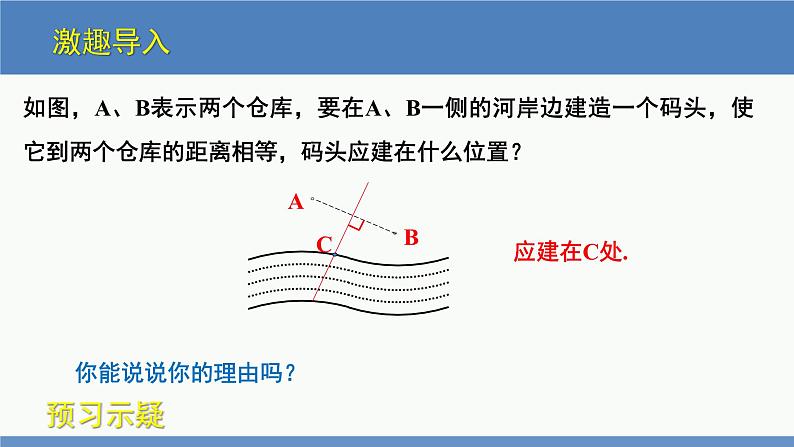
如图，A、B表示两个仓库，要在A、B一侧的河岸边建造一个码头，使它到两个仓库的距离相等，码头应建在什么位置？
1. 学会综合法证明线段的垂直平分线的性质定理和判断定理.（重点） 2.通过探索、发现、猜测、证明等过程，发展推理证明的能力、规范证明的书写格式.（难点）
探究一：线段垂直平分线的性质定理
我们曾经利用折纸的方法得到:线段垂直平分线上的点到这条线段两个端点距离相等.你能证明这一结论吗?
已知：如图，AC=BC，MN⊥AB，P是MN上任意一点. 求证：PA=PB．
证明：∵MN⊥AB，∴∠PCA=∠PCB=90°∵AC=BC，PC=PC，∴△PCA≌△PCB（SAS）；∴PA=PB（全等三角形的对应边相等）．
如果点P与点C重合，那么结论显然成立.
性质定理：线段垂直平分线上的点到这条线段的两端点的距离相等．
温馨提示：这个结论是经常用来证明两条线段相等的根据之一.
∵P在线段AB的垂直平分线上∴PA=PB
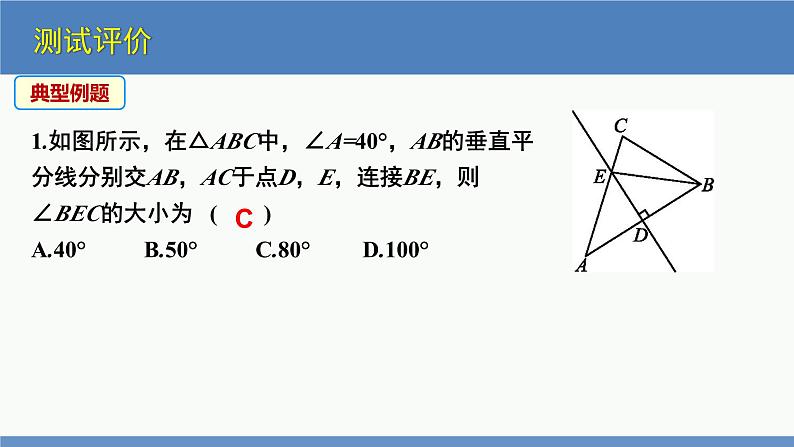
1.如图所示，在△ABC中，∠A=40°，AB的垂直平分线分别交AB，AC于点D，E，连接BE，则∠BEC的大小为(　　)A.40° B.50° C.80° D.100°
探究二：线段垂直平分线的性质定理的逆定理
逆命题：如果有一个点到线段两个端点的距离相等，那么这个点在这条线段的垂直平分线上，即到线段两个端点的距离相等的点在这条线段的垂直平分线上．
当我们写出逆命题时，就想到判断它的真假．如果真，则需证明它；如果假，则需用反例说明．
证明：（方法一）过点P作已知线段AB的垂线PC， ∵PA=PB，PC=PC，∴Rt△PAC≌Rt△PBC（HL），∴AC=BC，即P点在AB的垂直平分线上．
性质定理的逆命题：到线段两个端点的距离相等的点在这条线段的垂直平分线上．
（方法二）把线段AB的中点记为C,连接PC. ∵C为AB的中点， ∴AC=BC. ∵PA=PB,PC=PC， ∴△APC≌△BPC(SSS)， ∴∠PCA=∠PCB=90°， ∴PC⊥AB， 即P在AB的垂直平分线上.
注意：这个结论经常用来证明点在直线上（或直线经过某一点）的根据之一．
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
如图,∵PA=PB(已知),∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
如图所示，在△ABC中，∠ACB=90°，D是BC延长线上的一点，E是BD的垂直平分线与AB的交点，DE交AC于点F.求证:点E在AF的垂直平分线上.
证明: ∵E是BD的垂直平分线上一点,∴EB=ED,∴∠B=∠D.∵∠ACB=90°,∴∠A=90°-∠B,∠CFD=90°-∠D,∴∠CFD=∠A.又∵∠AFE=∠CFD,∴∠AFE=∠A,∴EF=EA,∴点E在AF的垂直平分线上.
解：∵DE为AB的垂直平分线， ∴AE=BE. ∵△BCE的周长等于50， ∴BE+EC+BC=50，即AE+EC+BC=50， ∴AC+BC=50. ∵AC=27， ∴BC=23.
3.有下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB，PA=PB；②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的是　　　　　　.(填序号)
证明：∵AB=AC，∴A在线段BC的垂直平分线上.∵BD=CD，∴ D在线段BC的垂直平分线上.∴ AD是线段BC的垂直平分线.∵P是AD上一点 ， ∴PB=PC.