2024年中考数学复习课件---微专题9 特殊四边形辅助线的做法

这是一份2024年中考数学复习课件---微专题9 特殊四边形辅助线的做法，共17页。PPT课件主要包含了类型清单，模型展示等内容，欢迎下载使用。

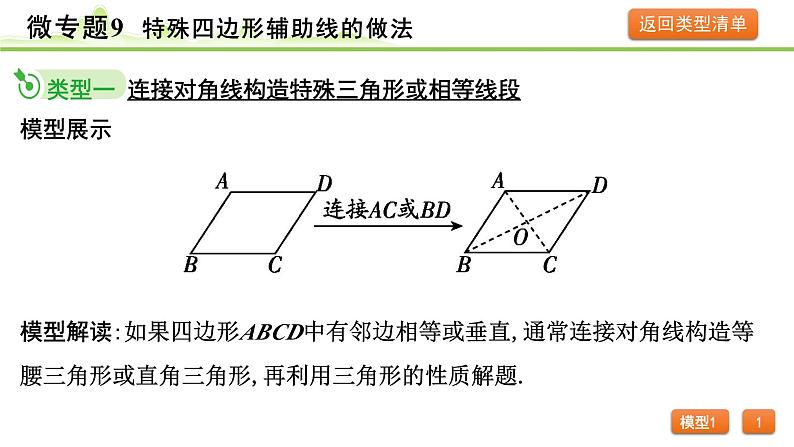
模型解读:如果四边形ABCD中有邻边相等或垂直,通常连接对角线构造等腰三角形或直角三角形,再利用三角形的性质解题.
1.如图,四边形ABCD是正方形,E,F是对角线AC上的两点,且AE=CF.(1)求证:四边形BEDF是菱形;
(2)若AC=8,AE=2,求四边形BEDF的周长.
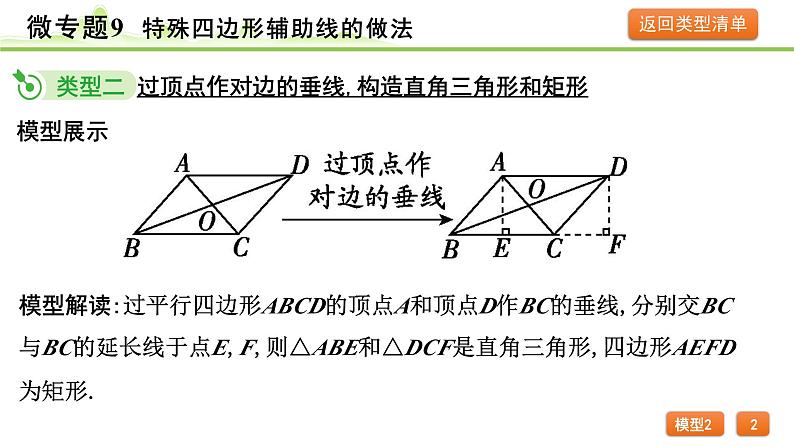
模型解读:过平行四边形ABCD的顶点A和顶点D作BC的垂线,分别交BC与BC的延长线于点E,F,则△ABE和△DCF是直角三角形,四边形AEFD为矩形.
2.(2022·贵阳观山湖区模拟改编)如图,若将▱DBEC沿BD折叠,点C恰好落在EB的延长线上点A处,连接AC,AD.已知AC=6,BD=8.(1)求△ACE的面积;
(2)若直线AE上有一点F,当△FCE为等腰三角形时,直接写出线段AF的长.
3.如图,在▱ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长为　　　　. 
模型解读:在▱ABCD中,如图1,E为AD边上的一点,连接CE与BD交于点F,则△BFC∽△DFE.如图2,点F为CD边上的一点,连接AF并延长交BC的延长线于点E,则△AFD∽△EFC.
4.如图,在矩形ABCD中,E是AB边的中点,F是AD边上一点,∠DFC=2∠FCE,CE=8,CF=10,则线段AF的长为　　　　. 
模型解读:在▱ABCD中,分别过点A,C作AE⊥BD于点E,CF⊥BD于点F,则AE∥CF,△ABE≌△CDF.
模型解读:①如图1,赵爽弦图中,△AED≌△BFA≌△CGB≌△DHC.②如图2,若DE⊥AF,则△DAE≌△ABF;如图3的矩形,若DE⊥AF,则△ABF∽△DAE.③当正方形中存在直角三角形时,常通过作垂线构造全等三角形,利用弦图模型进行线段和角的转化.
6.如图,E,F,G,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB=3, BC=4,则EF∶GH为　　　　.